Sparsifying Synchronization for High-Performance Shared-Memory Sparse Triangular Solver

Abstract

The last decade has seen rapid growth of single-chip multiprocessors (CMPs), which have been leveraging Moore’s law to deliver high concurrency via increases in the number of cores and vector width. Modern CMPs execute from several hundreds to several thousands concurrent operations per second, while their memory subsystem delivers from tens to hundreds Giga-bytes per second bandwidth.

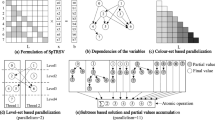
Taking advantage of these parallel resources requires highly tuned parallel implementations of key computational kernels, which form the back-bone of modern HPC. Sparse triangular solver is one such kernel and is the focus of this paper. It is widely used in several types of sparse linear solvers, and it is commonly considered challenging to parallelize and scale even on a moderate number of cores. This challenge is due to the fact that triangular solver typically has limited task-level parallelism and relies on fine-grain synchronization to exploit this parallelism, compared to data-parallel operations such as sparse matrix-vector multiplication.

This paper presents synchronization sparsification technique that significantly reduces the overhead of synchronization in sparse triangular solver and improves its scalability. We discover that a majority of task dependencies are redundant in task dependency graphs which are used to model the flow of computation in sparse triangular solver. We propose a fast and approximate sparsification algorithm, which eliminates more than 90% of these dependencies, substantially reducing synchronization overhead. As a result, on a 12-core Intel^® Xeon^® processor, our approach improves the performance of sparse triangular solver by 1.6x, compared to the conventional level-scheduling with barrier synchronization. This, in turn, leads to a 1.4x speedup in a pre-conditioned conjugate gradient solver.