Abstract
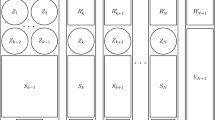
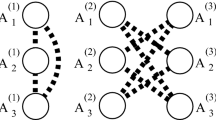
We study a graph coloring problem motivated by a fun Sudoku-style puzzle. Given a bipartition of the edges of a graph into near and far sets and an integer threshold t, a threshold-coloring of the graph is an assignment of integers to the vertices so that endpoints of near edges differ by t or less, while endpoints of far edges differ by more than t. We study threshold-coloring of tilings of the plane by regular polygons, known as Archimedean lattices, and their duals, the Laves lattices. We prove that some are threshold-colorable with constant number of colors for any edge labeling, some require an unbounded number of colors for specific labelings, and some are not threshold-colorable.
Supported in part by NSF grants CCF-1115971 and DEB 1053573.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Alam, M.J., Kobourov, S.G., Pupyrev, S., Toeniskoetter, J.: Happy edges: Threshold-coloring of regular lattices. Arxiv report arxiv.org/abs/1306.2053 (2013)
Alam, M. J., Chaplick, S., Fijavž, G., Kaufmann, M., Kobourov, S.G., Pupyrev, S.: Threshold-coloring and unit-cube contact representation of graphs. In: Brandstädt, A., Jansen, K., Reischuk, R. (eds.) WG 2013. LNCS, vol. 8165, pp. 26–37. Springer, Heidelberg (2013)
Albertson, M.O., Chappell, G.G., Kierstead, H.A., Kündgen, A., Ramamurthi, R.: Coloring with no 2-colored P 4. Electron. J. Combin. 11(1), R26 (2004)
Brandstädt, A., Le, V.B., Spinrad, J.P.: Graph classes: a survey. Society for Industrial and Applied Mathematics (1999)
Bremner, D., Evans, W., Frati, F., Heyer, L., Kobourov, S., Lenhart, W., Liotta, G., Rappaport, D., Whitesides, S.: On representing graphs by touching cuboids. In: Didimo, W., Patrignani, M. (eds.) GD 2012. LNCS, vol. 7704, pp. 187–198. Springer, Heidelberg (2013)
Eggleton, R.B., Erdös, P., Skilton, D.K.: Colouring the real line. Journal of Combinatorial Theory, Series B 39(1), 86–100 (1985)
Ferrara, M., Kohayakawa, Y., Rödl, V.: Distance graphs on the integers. Combinatorics, Probability and Computing 14, 107–131 (2005)
Fiala, J., Kloks, T., KratochvÃl, J.: Fixed-parameter complexity of λ-labelings. In: Widmayer, P., Neyer, G., Eidenbenz, S. (eds.) WG 1999. LNCS, vol. 1665, pp. 350–363. Springer, Heidelberg (1999)
Fiala, J., Kratochvìl, J., Proskurowski, A.: Systems of distant representatives. Discrete Applied Mathematics 145(2), 306–316 (2005)
Golumbic, M.C., Kaplan, H., Shamir, R.: Graph sandwich problems. Journal of Algorithms 19(3), 449–473 (1995)
Griggs, J.R., Yeh, R.K.: Labelling graphs with a condition at distance 2. SIAM Journal on Discrete Mathematics 5(4), 586–595 (1992)
Hammer, P.L., Peled, U.N., Sun, X.: Difference graphs. Discrete Applied Mathematics 28(1), 35–44 (1990)
Mahadev, N.V.R., Peled, U.N.: Threshold Graphs and Related Topics. North-Holland (1995)
Roberts, F.: From garbage to rainbows: Generalizations of graph coloring and their applications. Graph Theory, Combinatorics, and Applications 2, 1031–1052 (1991)
Timmons, C.: Star coloring high girth planar graphs. The Electronic Journal of Combinatorics 15(1), R124 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
Alam, M.J., Kobourov, S.G., Pupyrev, S., Toeniskoetter, J. (2014). Happy Edges: Threshold-Coloring of Regular Lattices. In: Ferro, A., Luccio, F., Widmayer, P. (eds) Fun with Algorithms. FUN 2014. Lecture Notes in Computer Science, vol 8496. Springer, Cham. https://doi.org/10.1007/978-3-319-07890-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-07890-8_3
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-07889-2
Online ISBN: 978-3-319-07890-8
eBook Packages: Computer ScienceComputer Science (R0)