Quantum Algorithms for Matrix Products over Semirings

Abstract

In this paper we construct quantum algorithms for matrix products over several algebraic structures called semirings, including the ( max , min )-matrix product, the distance matrix product and the Boolean matrix product. In particular, we obtain the following results.

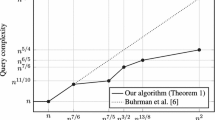
• We construct a quantum algorithm computing the product of two n×n matrices over the ( max , min ) semiring with time complexity O(n ^2.473). In comparison, the best known classical algorithm for the same problem has complexity O(n ^2.687). As an application, we obtain a O(n ^2.473)-time quantum algorithm for computing the all-pairs bottleneck paths of a graph with n vertices, while classically the best upper bound for this task is O(n ^2.687).

• We construct a quantum algorithm computing the ℓ most significant bits of each entry of the distance product of two n×n matrices in time O(2^0.64ℓ n ^2.46). In comparison, prior to the present work, the best known classical algorithm for the same problem had complexity O(2^ℓ n ^2.69). Our techniques lead to further improvements for classical algorithms as well, reducing the classical complexity to O(2^0.96ℓ n ^2.69), which gives a sublinear dependency on 2^ℓ.

The above two algorithms are the first quantum algorithms that perform better than the $\tilde O(n^{5/2})$-time straightforward quantum algorithm based on quantum search for matrix multiplication over these semirings. We also consider the Boolean semiring, and construct a quantum algorithm computing the product of two n×n Boolean matrices that outperforms the best known classical algorithms for sparse matrices.