Abstract
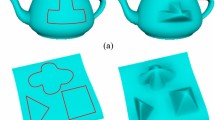
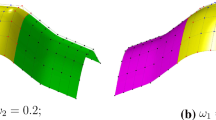
This paper describes the development of a free-form deformation model (FFD) which is an extension of the Scodef model of geometric constraint-based deformations. The deformation is applied to a point over the surface and it is restricted to a region which is limited by a closed B-Spline curve acting as a profile. The main difference from the original model is that in the new one, the conditions to define restrictions with non rectilinear trajectories have been established. These conditions are represented by 4D B-Spline curves. With the proposed solution, the deformed surface is adjusted precisely as described by both B-Spline curves. The model has been called N-Scodef.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bechmann, D., Gerber, D.: Arbitrary shaped deformations with DOGME. The Visual Computer 19, 175–186 (2003), http://dx.doi.org/10.1007/s00371-002-0191-x176 , 10.1007/s00371-002-0191-x176
Borrel, P., Bechmann, D.: Deformation of n–dimensional objects. In: Proceedings of the First ACM Symposium on Solid Modeling Foundations and CAD/CAM Applications, SMA 1991, pp. 351–369. ACM, New York (1991)
Borrel, P., Rappoport, A.: Simple constrained deformations for geometric modeling and interactive design. ACM Transactions on Graphics 13(2), 137–155 (1994)
Clapés, M., González-Hidalgo, M., Mir-Torres, A., Palmer-Rodríguez, P.A.: Interactive constrained deformations of NURBS surfaces: N-SCODEF. In: Perales, F.J., Fisher, R.B. (eds.) AMDO 2008. LNCS, vol. 5098, pp. 359–369. Springer, Heidelberg (2008), http://www.springerlink.com/content/755x0m42567u22k0/
Jin, X., Li, Y., Peng, Q.: General constrained deformations based on generalized metaballs. Computer & Graphics 24, 200 (2000)
La Gréca, R.: Approche déclarative de la modélisation de surfaces. Ph.D. thesis. Université de la Méditerranée Aix–Marseille II (2005)
La Gréca, R., Raffin, R., Gesquière, G.: Punctual constraint resolution and deformation path on NURBS. In: International Conference on Computer Graphics and Vision, Graphicon 2007 (2007), http://www.graphicon.ru/2007/proceedings/Papers/Paper_38.pdf
Lanquetin, S., Raffin, R., Neveu, M.: Generalized SCODEF deformations on subdivision surfaces. In: Perales, F.J., Fisher, R.B. (eds.) AMDO 2006. LNCS, vol. 4069, pp. 132–142. Springer, Heidelberg (2006)
Piegl, L., Tiller, W.: The NURBS Book, Monographs in visual communications, 2nd edn. Springer (1997)
Brecher, C., Lindemann, D., Merz, M., Wenzel, C., Preuß, W.: Free form deformations or deformations non-constrained by geometries or topologies. In: Brinksmeier, E., Riemer, O., Gläbe, R. (eds.) Fabrication of Complex Optical Components. Lecture Notes in Computational Vision and Biomechanics, vol. 7, pp. 49–74. Springer, Netherlands (2013), http://dx.doi.org/10.1007/978-94-007-5446-1_2
Raffin, R., Gesquière, G., La Gréca, R.: Déformations de modèles géométriques. Tech. Rep. LSIS.RR.2007.001, LSIS (2007)
Raffin, R., Neveu, M., Derdouri, B.: Constrained deformation for geometric modeling and object reconstruction. In: WSCG 1998 – International Conference in Central Europe on Computer Graphics, Visualization 1998, vol. 2, pp. 299–306 (1998)
Raffin, R., Neveu, M., Jaar, F.: Extended constrained deformations: A new sculpturing tool. In: Proceedings of International Conference on Shape Modeling International 1999, pp. 219–224 (March 1999)
Raffin, R., Neveu, M., Jaar, F.: Curvilinear displacement of free–form–based deformation. The Visual Computer 16, 38–46 (2000), http://dx.doi.org/10.1007/s003710050005 , 10.1007/s003710050005
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
González-Hidalgo, M., Mir-Torres, A., Palmer-Rodríguez, P. (2014). Geometric Surface Deformation Based on Trajectories: A New Approach. In: Perales, F.J., Santos-Victor, J. (eds) Articulated Motion and Deformable Objects. AMDO 2014. Lecture Notes in Computer Science, vol 8563. Springer, Cham. https://doi.org/10.1007/978-3-319-08849-5_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-08849-5_18
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-08848-8
Online ISBN: 978-3-319-08849-5
eBook Packages: Computer ScienceComputer Science (R0)