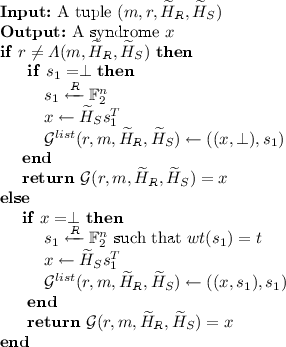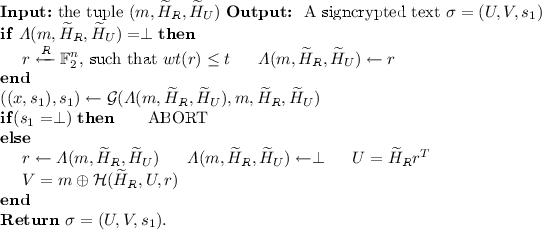A Provably Secure Signature and Signcryption Scheme Using the Hardness Assumptions in Coding Theory

Abstract

Signcryption is a cryptographic protocol that provides authentication and confidentiality as a single primitive at a cost lower than the combined cost of sign and encryption. Code-based cryptography, a likely candidate for post-quantum cryptography, provides an exciting alternative to number-theoretic cryptography. Courtois, Finiasz and Sendrier proposed the only practical code-based signature(CFS signature) at Asiacrypt 2001. But that signature scheme currently lacks a formal proof of security due to the existence of the high rate distinguisher proposed by Faugère et al. In this paper, we make use of an alternate key-construct for the CFS signature, and thus prove its existential unforgeability under chosen message attacks (EUF-CMA). Also, we propose a code-based signcryption scheme and prove its security. To the best of our knowledge, this is the first code-based, provably secure signature and signcryption scheme in literature.

A Proof of Confidentiality for the Signcryption Scheme

Theorem 4

(Confidentiality). The given scheme is secure in the sense of SC-IND-CCA2 (under the random oracle model) if the syndrome decoding ($\mathsf SD$) is hard to solve and the public key is computationally indistinguishable from the parity matrix of a random $(n,k-1,t)$ code $R$.

Proof: We build the proof, by constructing a challenger $\mathcal {C}$ through a sequence of games Game0, Game1, $\cdots$. Game0 is the adaptation of the protocol to the SC-IND-CCA2 game. Successive games are obtained by small modifications of the preceding games, in such a way that the difference of the adversarial advantage in consecutive games is easily quantifiable.

Let $q_{\mathcal {H}}, q_{\mathcal {G}},q_s,q_u$ be the maximum number of queries made by the adversary $\mathcal {A}$ to the oracles for the hash queries $\mathcal {H},\mathcal {G}$, the signcryption oracle and the de-signcryption oracle. We want to show that the advantage for the adversary $\mathcal {A}$ is bounded by the advantage of solving the hard problem $\mathsf{SD }$ for a random code with parity check matrix $R$.

To answer the hash queries and the signcryption and the de-signcryption queries, we maintain the lists, $\mathcal {G}^{list},\mathcal {H}^{list},\sigma ^{list}$ and $\varLambda$. If there is no value in a list we denote its output by $\perp$.

• The list $\mathcal {G}^{list}$ contains a tuple ($(x,s),a$) indexed by ($r,m,\widetilde{H}_R,\widetilde{H}_S$).

• The list $\mathcal {H}^{list}$ consists of strings $\rho \in \{0,1\}^l$ indexed by ($\widetilde{H}_R, U,r$) where $\widetilde{H}_R$ and $\widetilde{H}_S$ are $(n-k) \times n$ sized parity check matrices, and $U \in \mathbb {F}_2^{n-k}$ and $r \in \mathbb {F}_2^n$ such that $wt(r) \le t$.

• The $\sigma ^{list}$ (the signature list) consists of entries of the form ($m,\sigma =(U,V,s)$).

• The list $\varLambda$ consists of indices $r$ of $\varLambda (m)$ for which the simulator is able to produce a signature on $\mathcal {G}(m,\varLambda (m,\widetilde{H}_R,\widetilde{H}_S)),\widetilde{H}_R,\widetilde{H}_S)$, i.e., the list of $r$ for which $\mathcal {G}(m,\varLambda (m,\widetilde{H}_R,\widetilde{H}_S)),\widetilde{H}_R,\widetilde{H}_S)$ is a decodable syndrome.

• Game 0. This is the standard SC-IND-CCA2 game. The private and public key pair are obtained by running the key generation algorithm given the scheme, to obtain secret key ($Q_U,H_U,P_U,H'_U$), where $H_U \leftarrow \mathsf {Goppa}(n,k)$ ( a binary Goppa code), and the public key $\widetilde{H}_U =Q'_UH_UP_U \oplus a_Ub_U^T$. $\widetilde{H}_U$ is given to $\mathcal {A}$. Also, $\mathcal {A}$ is given access to the hash oracles $\mathcal {H}$ and $\mathcal {G}$. The signcryption oracle and designcryption oracle function as mentioned in the scheme. Let $X_0$ be the event that $\mathcal {A}$ wins Game 0. It is seen that Game 0 runs the SC-IND-CCA2 game on the proposed scheme perfectly.

  Therefore $Pr[X_0] - \frac{1}{2} = Adv^{ind-cca}_{\mathcal {A}}(n,k)$.

• Game 1. (Simulation of hash oracles) In this game, the hash oracles for $\mathcal {G}$ and $\mathcal {H}$ are simulated, while the rest of the protocol is executed as in the previous game. The two oracles are simulated as follows:

  For the query on $\mathcal {G}$ of the form ($r, m, \widetilde{H}_R,\widetilde{H}_S$), we have two situations, depending on whether $r=\varLambda (m,\widetilde{H}_R,\widetilde{H}_S)$. The simulation of the oracle is given below:

  

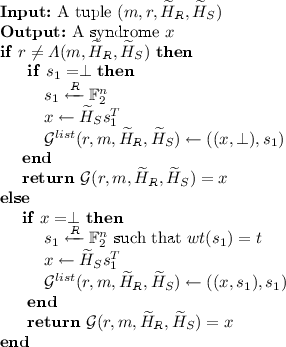
  For the query to $\mathcal {H}$ of the form ($\widetilde{H}_R,U,r$), the challenger searches $\mathcal {H}^{list}$ for the tuple ($\widetilde{H}_R,U,r$). If found, the corresponding value from the list is returned, else return a random string $\rho \xleftarrow []{R} \{0,1\}^l$ and store the tuple (($\widetilde{H}_R,U,r$),$\rho$) in $\mathcal {H}^{list}$. Let $X_1$ be the event that $\mathcal {A}$ wins Game 1.It is seen that, while the oracles are simulated in Game 1, the distribution of the output of these oracles remain unchanged (i.e., the randomness is maintained) from Game 0.

  Hence $Pr[X_1]=Pr[X_0]$

• Game 2. (Simulation of the signcryption oracle.) The signcryption oracle is simulated as follows:

  

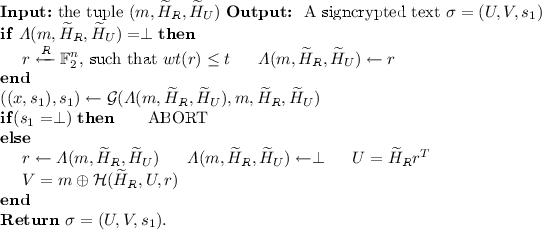
  The simulation of the signcryption is an extension of the signing oracle simulation presented in the previous proof. It is thus, seen that the $s_1$ is a valid signature on $m$ for verification key $\widetilde{H}_U$. Also, the remaining signcrypted text is also valid, and follows from the signcrypt algorithm given in the scheme. In Game 2, incoherence occurs if the oracle to $\mathcal {G}$ is queried initially for some $(r,m,\widetilde{H}_R,\widetilde{H}_S)$ such that later $r$ is set to $\varLambda (m,\widetilde{H}_R,\widetilde{H}_S)$. This happens with the probability $\frac{q_s}{\left( \begin{array}{c} n \\ t \end{array}\right) }$ (since the indices $\varLambda$ are defined only when the signcryption oracle is queried). It can be noted that this incoherence is the only scenario in which $\mathcal {F}$ can distinguish Game 2 from Game 1. Therefore, for the event $X_2$,that $\mathcal {A}$ wins the Game 2, we obtain, $|Pr[X_1] - Pr[X_2]| \le \frac{q_s}{\left( \begin{array}{c} n \\ t \end{array}\right) }.$

• Game 3. (Simulation of the designcryption oracle.) For the designcryption oracle queried on ($s_1,U,V,\widetilde{H}_U,\widetilde{H}_S$) the following is done:

  • The challenger searches the $\mathcal {H}^{list}$ for the tuple ($\widetilde{H}_U,U,\lambda$) such that $\widetilde{H}_U\lambda ^T=U$. If it exists in the list, then the corresponding vector $X$ is given as output. If no such tuple is found (i.e., the hash for such a tuple has not been queried) then it fixes $\lambda =\perp$ and gives the corresponding output from the hash oracle as $X$.

  • It obtains $m' =V \oplus X$.

  • The challenger then searches $\mathcal {G}^{list}$ for the tuple of the form $(\lambda ,m',\widetilde{H}_U,\widetilde{H}_S)$ where $\widetilde{H}_U\lambda ^T=U$ or $\lambda = \perp$. If the tuple is not in $\mathcal {G}^{list}$, the challenger adds it to the list.

  • Now the challenger verifies if $\widetilde{H}_U{s_{1}}^T \mathop {=}\limits ^{?} \mathcal {G}( \lambda ,m',\widetilde{H}_U,\widetilde{H}_S)$. If the condition holds and $\widetilde{H}_U \lambda ^T = U$, then the challenger returns $m'$ as the message. If condition holds but $\lambda =\perp$ then challenger ABORTS citing failure. If the condition does not hold at all, then the challenger returns $\perp$, as symbol of rejection of invalid signcrypted text.

  In the above game, if the challenger aborts, it implies that the adversary created the signcrypted text without querying the hash oracles. Hence, the probability of aborting is $\frac{q_d}{2^l}$., This scenario (of ABORT) would not occur in Game 2. Hence, for the event $X_3$ that $\mathcal {A}$ wins Game 3, we have $|Pr[X_3]-Pr[X_2]| \le \frac{q_d}{2^l}$.

• Game 4. (Changing the key generation algorithm) The adversary has access to the private keys of all users except the user $U$. Hence, for the other users, the keys are generated as in the scheme, and given to the adversary. For the user $U$, $\mathcal {C}$ selects the private key $H_U= R$. The public key is $\widetilde{H}_U = R'$, where $R'^T = [R^T|z^T]$ where $z \in _R \mathbb {F}_2^{n}$. The verification key $\widetilde{H}_U$ is given to the adversary $\mathcal {A}$. It follows from Assumption 2 that $|Pr[X_3] - Pr[X_4]| \le \mathsf Adv ^\mathsf{Dist }_{\mathcal {C}}(n,k)$ where $X_4$ is the event that $\mathcal {A}$ wins Game 4.

• Game 5. (Challenge ciphertext) The challenger takes the message $m_b$, and does the following to create the challenge, which would aid the challenger in solving the problem instance, syndrome $s$ (where $wt(s) > 2t+1$). The challenger wants to find $r \in \mathbb {F}_2^n$ with $wt(r) \le t$ such that $s = Rr^T$. The challenger generates the challenge cipher-text as follows:

  • $C$ sets $U^* = s'$, where $s'^T = [s^T|s_c]$ where $s_c$ is a randomly generated bit.

  • For the query on $\mathcal {H}$, $\mathcal {C}$ sets a special symbol $\top$, randomly generates a vector $y$ and stores it in $\mathcal {H}^{list}$ as $(\widetilde{H}_U, U^*,\top ,y)$. And for the query on $\mathcal {G}$, again uses the special symbol $\top$, also a random decodable syndrome (say $x$, with the decoded vector $s_1$) is given (just as in the simulation in $\mathcal {G}$ oracle and the Signcrypt oracle), and stores in $\mathcal {G}^{list}$ the tuple $(m_b,\top ,\widetilde{H}_U,\widetilde{H}_S,(x,s_1),s_1)$. The signing is simulated just as in signcryption oracle.

  • The challenger set $V=m_b \oplus y$.

  Also, the challenger has to now alter the answer to the hash queries in the following way:

  • For the $\mathcal {H}$ oracle, for any query $(\widetilde{H}_U,\widetilde{H}_Us^T,r)$ where $\widetilde{H}_Ur^T \ne \widetilde{H}_Us^T$, some random value is returned. If $\widetilde{H}_Ur^T = U^*$ and $weight(r) \le t$, then the value $y$ is returned, and $\top$ is replaced by $r$ in the tuple. The valid $r$ thus obtained is the solution to the problem instance.

  • For the $\mathcal {G}$ oracle, for any query $(m,r,\widetilde{H}_U,\widetilde{H}_S)$ if $\widetilde{H}_Ur^T = U^*$ and $m=m_b$ output $x$,else output any random syndrome. The valid $r$ thus obtained is the solution to the problem instance.

  Just as in the proof of unforgeability, the decodability of $U^*$ depends on correctly predicting $s_c$, which occurs with probability $\frac{1}{2}$. If $X_5$ be the event that $\mathcal {A}$ wins Game 5, we can clearly claim that, $|Pr[X_4] - Pr[X_5]| \le \mathsf {Adv}^{SD}_{\mathcal {C}}(n,k)/2$ where $\mathsf {Adv}^{SD}_{\mathcal {C}}(n,k)$ is the advantage that some $PPT$ algorithm $\mathcal {C}$ has at solving the syndrome decoding problem ($\mathsf {SD}$) on $R$.

• Game 6. (Challenge ciphertext) In this game, the challenger $C$ again alters the procedure of producing the challenge ciphertext. For the ciphertext, the process of creating $U$ and $s$ is the same, but changes for $V$. The challenger $C$ sets $V=z$,where $z \xleftarrow []{R} \{0,1\}^l$. Clearly, now the challenge ciphertext generated is completely random. But, even in game 5, the ciphertext generated was random as we blinded the message with a completely random component. Hence, there is no change in the distribution of the ciphertext space, i.e., $Pr[X_5] = Pr[X_6]$, where $X_6$ is the event that $\mathcal {A}$ wins Game 6. Also, it can noted that the probability of correctly guessing the choice $b$ by the adversary $\mathcal {A}$ is exactly half, i.e., $Pr[X_6] =\frac{1}{2}$.

Accumulating all the above results and using triangular inequality we have the following result: $Adv^{ind-cca2}(\mathcal {A}) \le \frac{q_s}{\left( \begin{array}{c} n \\ t \end{array}\right) }+\frac{q_d}{2^l}+ \mathsf{Adv }^\mathsf{Dist }_{\mathcal {C}}(n,k)+ \mathsf {Adv}^{SD}_{\mathcal {C}}(n,k)/2$. Hence, the advantage of the adversary is bound by the advantage of the challenger in solving the syndrome decoding problem and the weak distinguishability.       $\square$