Abstract
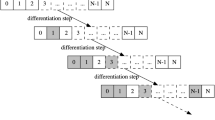
The characterization of the generic properties underlying the complex interplay ruling cell differentiation is one of the goals of modern biology. To this end, we rely on a powerful and general dynamical model of cell differentiation, which defines differentiation hierarchies on the basis of the stability of gene activation patterns against biological noise.
In particular, in this work we investigate the role of the topology (i.e. scale-free or random) and of the dynamical regime (i.e. ordered, critical or disordered) of gene regulatory networks on the model dynamics. Two real lineage commitment trees, i.e. intestinal crypts and hematopoietic cells, are compared with the hierarchies emerging from the dynamics of ensembles of randomly simulated networks.
Briefly, critical networks with random topology seem to display a wider range of possible behaviours as compared to the others, hence suggesting an intrinsic dynamical heterogeneity that may be fundamental in defining different differentiation trees. Conversely, scale-free networks show a generally more ordered dynamics, which limit the overall variability, yet containing the effect of possible genomic perturbations. Interestingly, a considerable number of networks across all types show emergent trees that are biologically plausible, suggesting that a relatively wide portion of the networks space may be suitable, without the need for a fine tuning of the parameters.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Given a GRN dynamical model, the long term evolution will confine the cellular states in a specific region of the state space, i.e. an attractor, in which the values of the variables can be fixed over time, can be characterized by oscillatory periodic regimes, or even by more particular non-periodic dynamics (in non finite-states deterministic models). Any GRN can be characterized by the presence of different attractors, reachable from distinct initial conditions. The attractors represent coherent activation patterns of genes.
- 2.
Cell differentiation is the process according to which the progeny of stem cells progressively develops into different and always more specialized cell types, crossing various intermediate stages.
- 3.
Excluding the high degree exponential cutoffs due to the limited size of the networks.
- 4.
We here use the so called quenched model [21], in which both the graph and the boolean functions do not change in time.
- 5.
In several processes, e.g., during the embryogenesis, cell differentiation is not stochastic but it is driven towards precise, repeatable types by specific chemical signals. In our model, it was shown that certain genes, called switch genes, if permanently perturbed and coupled with a change in the threshold always leads the system through the same differentiation pathway. In other words, nodes that uniquely determine to which TES the system will evolve, i.e. deterministic differentiation.
- 6.
For each level of the input tree, the algorithm compares the distribution of the number of children of the two trees. The histogram distance is then defined as the sum of the absolute value of the difference between the number of nodes in the first tree with \(i\) children in the two trees, from \(i =1\) to the maximum number of children. The overall distance is the sum of all the histogram distances of the distinct levels.
- 7.
It is worth noticing that an attractor has always been reached within the simulation time.
References
Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K., Walter, P.: Molecular Biology of the Cell, 5th edn. Garland Science, New York (2007)
Aldana, M., Coppersmith, S., Kadanoff, L.: Boolean dynamics with random couplings. In: Kaplan, E., Marsden, J., Sreenivasan, K.R. (eds.) Perspectives and Problems in Nonlinear Science: Springer Applied Mathematical Sciences Series. Springer, New York (2003)
Barabasi, A.-L., Albert, R.: Emergence of scaling in random networks. Science 286, 509–512 (1999)
Blake, W.J., Mads, K., Cantor, C.R., Collins, J.J.: Noise in eukaryotic gene expression. Nature 422, 633–637 (2003)
Damiani, C., Graudenzi, A., Serra, R., Villani, M., Colacci, A., Kauffman, S.A.: On the fate of perturbations in critical random boolean networks. In: Proceedings of the European Conference on Complex Systems, ECCS 2009 (Cd-rom) (2009)
De Matteis, G., Graudenzi, A., Antoniotti, M.: A review of spatial computational models for multi-cellular systems, with regard to intestinal crypts and colorectal cancer development. J. Math. Biol. 66(7), 1409–1462 (2013)
Degasperi, A., Gilmore, S.: Sensitivity analysis of stochastic models of bistable biochemical reactions. In: Bernardo, M., Degano, P., Zavattaro, G. (eds.) SFM 2008. LNCS, vol. 5016, pp. 1–20. Springer, Heidelberg (2008)
Eldar, A., Elowitz, M.B.: Functional roles for noise in genetic circuits. Nature 467, 167–173 (2010)
Erdos, P., Rényi, A.: On the evolution of random graphs. Bull. Inst. Int. Statist 38(4), 343–347 (1961)
Furusawa, C., Kaneko, K.: Chaotic expression dynamics implies pluripotency: When theory and experiment meet. Biol. Direct. 4, 17 (2009)
Hayashi, K., Lopes, S.M., Surani, M.A.: Dynamic equilibrium and heterogeneity of mouse pluripotent stem cells with distinct functional and epigenetic states. Cell Stem Cell 3, 391–440 (2008)
Hoffman, M., Chang, H.H., Huang, S., Ingber, D.E., Loeffler, M., Galle, J.: Noise driven stem cell and progenitor population dynamics. PLoS ONE 3, e2922 (2008)
Hu, M., Krause, D., Greaves, M., Sharkis, S., Dexter, M., Heyworth, C., Enver, T.: Multilineage gene expression precedes commitment in the hemopoietic system. Genes Dev. 11, 774–785 (1997)
Huang, S., Ernberg, I., Kauffman, S.A.: Cancer attractors: A systems view of tumors from a gene network dynamics and developmental perspective. Semin Cell Dev Biol. 20(7), 869–876 (2009)
Huang, S., Guo, Y.P., Enver, T.: Bifurcation dynamics in lineage-commitment in bipotent progenitor cells. Dev. Biol. 305, 695–713 (2007)
Kalmar, T., Lim, C., Hayward, P., Munñoz-Descalzo Arias, S., Nichols, J., Garcia-Ojalvo, J., Martinez, A.: Regulated fluctuations in nanog expression mediate cell fate decisions in embryonic stem cells. PLoS Biol. 7, e1000149 (2009)
Sundaram, S., Sundararajan, N., Savitha, R.: Introduction. In: Sundaram, S., Sundararajan, N., Savitha, R. (eds.) Supervised Learning with Complex-valued Neural Networks. SCI, vol. 421, pp. 1–30. Springer, Heidelberg (2013)
Kashiwagi, A., Urabe, I., Kaneko, K., Yomo, T.: Adaptive response of a gene network to environmental changes by fitness-induced attractor selection. PLoS ONE 1, e49 (2006)
Kauffman, S.A.: Homeostasis and differentiation in random genetic control networks. Nature 224, 177 (1969)
Kauffman, S.A.: Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22, 437–467 (1969)
Kauffman, S.A.: At Home in the Universe. Oxford University Press, New York (1995)
Kauffman, S.A., Peterson, C., Samuelsson, B., Troein, C.: Random boolean network models and the yeast transcriptional network. Proc. Natl Acad. Sci. USA 100, 14796–14799 (2003)
Langton, C.G.: Life at the edge of chaos. In: Langton, C.G., Taylor, C., Farmer, J.D., Rasmussen, S. (eds.) Artificial Life II, pp. 41–91. Addison-Wesley, Reading (1992)
Lestas, I., Paulsson, J., Vinnicombe, G.: Noise in gene regulatory networks. IEEE Trans. Autom. Control 53, 189–200 (2008)
Mc Adams, H.H., Arkin, A.: Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA 94, 814–819 (1997)
Miyamoto, T., Iwasaki, H., Reizis, B., Ye, M., Graf, T., Weissman, I.L., Akashi, K.: Myeloid or lymphoid promiscuity as a critical step in hematopoietic lineage commitment. Dev. Cell. 3, 137–147 (2002)
Peixoto, T.P., Drossel, B.: Noise in random boolean networks. Phys. Rev. E 79, 036108–17 (2009)
Raj, A., van Oudenaarden, A.: Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell 135, 216–226 (2008)
Ramo, P., Kesseli, Y., Yli-Harja, O.: Perturbation avalanches and criticality in gene regulatory networks. J. Theor. Biol. 242, 164–170 (2006)
Ribeiro, A.S., Kauffman, S.A.: Noisy attractors and ergodic sets in models of gene regulatory networks. J. Theor. Biol. 247, 743–755 (2007)
Serra, R., Villani, M., Barbieri, A., Kauffman, S.A., Colacci, A.: On the dynamics of random boolean networks subject to noise: Attractors, ergodic sets and cell types. J. Theor. Biol. 265, 185–193 (2010)
Serra, R., Villani, M., Graudenzi, A., Colacci, A., Kauffman, S.A.: The simulation of gene knock-out in scale-free random boolean models of genetic networks. Netw. Heterogen. Med. 3(2), 333–343 (2008)
Serra, R., Villani, M., Graudenzi, A., Kauffman, S.A.: Why a simple model of genetic regulatory networks describes the distribution of avalanches in gene expression data. J. Theor. Biol. 249, 449–460 (2007)
Serra, R., Villani, M., Semeria, A.: Genetic network models and statistical properties of gene expression data in knock-out experiments. J. Theor. Biol. 227, 149–157 (2004)
Serra, R., Villani, M., Agostini, L.: On the dynamics of random boolean networks with scale-free outgoing connections. Physica A: Statistical Mechanics and its Applications 339, 665–673 (2004)
Shmulevich, I., Kauffman, S.A., Aldana, M.: Eukaryotic cells are dynamically ordered or critical but not chaotic. Proc. Natl. Acad. Sci. USA 102, 13439–13444 (2005)
Swains, P.S., Elowitz, M.B., Siggia, E.D.: Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA 99, 12795–12800 (2002)
Vijesh, N., Chakrabarti, S.K., Sreekumar, J.: Modeling of gene regulatory networks: A review. J. Biomed. Sci. Eng. 6, 223–231 (2013)
Villani, M., Barbieri, A., Serra, R.: A dynamical model of genetic networks for cell differentiation. PLoS ONE 6(3), e17703 (2011). doi:10.1371/journal.pone.0017703
Warren, L., Bryder, D., Weissman, I.L., Quake, S.R.: Transcription factor profiling in individual hematopoietic progenitors by digital RT-PCR. PNAS 103(47), 17807–17812 (2006)
Yamanaka, H.: Elite and stochastic models for induced pluripotent stem cell generation. Nature 460, 49–52 (2009)
Acknowledgements
This work was partially supported by the project SysBionet (12-4-5148000-15; Imp. 611/12; CUP: H41J12000060001; U.A. 53).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
Graudenzi, A. et al. (2014). Investigating the Role of Network Topology and Dynamical Regimes on the Dynamics of a Cell Differentiation Model. In: Pizzuti, C., Spezzano, G. (eds) Advances in Artificial Life and Evolutionary Computation. WIVACE 2014. Communications in Computer and Information Science, vol 445. Springer, Cham. https://doi.org/10.1007/978-3-319-12745-3_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-12745-3_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-12744-6
Online ISBN: 978-3-319-12745-3
eBook Packages: Computer ScienceComputer Science (R0)