Skip to main content
Springer Nature Link
Log in

Color Image Segmentation by Minimal Surface Smoothing

  • Conference paper
Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR 2015)

Part of the book series: Lecture Notes in Computer Science ((LNIP,volume 8932))

  • 2725 Accesses

Abstract

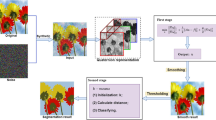
In this paper, we propose a two-stage approach for color image segmentation, which is inspired by minimal surface smoothing. Indeed, the first stage is to find a smooth solution to a convex variational model related to minimal surface smoothing. The classical primal-dual algorithm can be applied to efficiently solve the minimization problem. Once the smoothed image u is obtained, in the second stage, the segmentation is done by thresholding. Here, instead of using the classical K-means to find the thresholds, we propose a hill-climbing procedure to find the peaks on the histogram of u, which can be used to determine the required thresholds. The benefit of such approach is that it is more stable and can find the number of segments automatically. Finally, the experiment results illustrate that the proposed algorithm is very robust to noise and exhibits superior performance for color image segmentation.

This work is supported in part by the National Science Foundation of China (11271049), by HKRGC 211710 and 211911, by the FRGs of Hong Kong Baptist University, and by the HKPFS from HKRGC.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Acar, R., Vogel, C.R.: Analysis of bounded variation penalty methods for ill-posed problems. Inverse Problems 10(6), 1217–1229 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  2. Achanta, R., Estrada, F.J., Wils, P., Süsstrunk, S.: Salient region detection and segmentation. In: Gasteratos, A., Vincze, M., Tsotsos, J.K. (eds.) ICVS 2008. LNCS, vol. 5008, pp. 66–75. Springer, Heidelberg (2008)

    Chapter  Google Scholar 

  3. Ambrosio, L., Fusco, N., Pallara, D.: Functions of bounded variation and free discontinuity problems, vol. 254. Clarendon Press Oxford (2000)

    Google Scholar 

  4. Bae, E., Lellmann, J., Tai, X.-C.: Convex relaxations for a generalized chan-vese model. In: Heyden, A., Kahl, F., Olsson, C., Oskarsson, M., Tai, X.-C. (eds.) EMMCVPR 2013. LNCS, vol. 8081, pp. 223–236. Springer, Heidelberg (2013)

    Chapter  Google Scholar 

  5. Bae, E., Yuan, J., Tai, X.C.: Global minimization for continuous multiphase partitioning problems using a dual approach. International Journal of Computer Vision 92(1), 112–129 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  6. Boykov, Y., Kolmogorov, V.: Computing geodesics and minimal surfaces via graph cuts. In: Proceedings of the Ninth IEEE International Conference on Computer Vision, pp. 26–33. IEEE (2003)

    Google Scholar 

  7. Bresson, X., Chan, T.F.: Fast dual minimization of the vectorial total variation norm and applications to color image processing. Inverse Problems and Imaging 2(4), 455–484 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  8. Brown, E.S., Chan, T.F., Bresson, X.: Completely convex formulation of the chan-vese image segmentation model. International journal of computer vision 98(1), 103–121 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  9. Cai, X., Chan, R., Zeng, T.: A two-stage image segmentation method using a convex variant of the mumford–shah model and thresholding. SIAM Journal on Imaging Sciences 6(1), 368–390 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  10. Caselles, V., Kimmel, R., Sapiro, G.: Geodesic active contours. International Journal of Computer Vision 22(1), 61–79 (1997)

    Article  MATH  Google Scholar 

  11. Caselles, V., Kimmel, R., Sapiro, G., Sbert, C.: Minimal surfaces: A geometric three dimensional segmentation approach. Numerische Mathematik 77(4), 423–451 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  12. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision 40(1), 120–145 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  13. Chan, R., Yang, H., Zeng, T.: A two-stage image segmentation method for blurry images with poisson or multiplicative gamma noise. SIAM Journal on Imaging Sciences 7(1), 98–127 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  14. Chan, T.F., Esedoglu, S., Nikolova, M.: Algorithms for finding global minimizers of image segmentation and denoising models. SIAM Journal on Applied Mathematics 66(5), 1632–1648 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  15. Chan, T.F., Vese, L.A.: Active contours without edges. IEEE Transactions on Image Processing 10(2), 266–277 (2001)

    Article  MATH  Google Scholar 

  16. Deimling, K.: Nonlinear functional analysis. Courier Dover Publications (2013)

    Google Scholar 

  17. Ding, Z., Jia, J., Li, D.: Fast clustering segmentation method combining hill-climbing for color image (2011)

    Google Scholar 

  18. Goldstein, T., Osher, S.: The split bregman method for l1-regularized problems. SIAM Journal on Imaging Sciences 2(2), 323–343 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  19. Hu, Y.: Hill-climbing color image segmentation (2008), http://www.mathworks.com/matlabcentral/fileexchange/22274-hill-climbing-color-image-segmentation

  20. Jin, R., Kou, C., Liu, R., Li, Y.: A color image segmentation method based on improved k-means clustering algorithm. In: Zhong, Z. (ed.) Proceedings of the International Conference on Information Engineering and Applications (IEA) 2012. LNEE, vol. 217, pp. 499–505. Springer, Heidelberg (2013)

    Chapter  Google Scholar 

  21. Kimmel, R.: Numerical geometry of images: Theory, algorithms, and applications. Springer (2004)

    Google Scholar 

  22. Kluzner, V., Wolansky, G., Zeevi, Y.Y.: Minimal surfaces, measure-based metric and image segmentation. Technion-IIT, Department of Electrical Engineering (2006)

    Google Scholar 

  23. Kluzner, V., Wolansky, G., Zeevi, Y.Y.: Geometric approach to measure-based metric in image segmentation. Journal of Mathematical Imaging and Vision 33(3), 360–378 (2009)

    Article  MathSciNet  Google Scholar 

  24. Li, C., Xu, C., Gui, C., Fox, M.D.: Level set evolution without re-initialization: a new variational formulation. In: IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2005, vol. 1, pp. 430–436. IEEE (2005)

    Google Scholar 

  25. Li, F., Ng, M.K., Zeng, T.Y., Shen, C.: A multiphase image segmentation method based on fuzzy region competition. SIAM Journal on Imaging Sciences 3(3), 277–299 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  26. Martin, D., Fowlkes, C., Tal, D., Malik, J.: A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proc. 8th Int’l Conf. Computer Vision, vol. 2, pp. 416–423 (2001)

    Google Scholar 

  27. Mumford, D., Shah, J.: Optimal approximations by piecewise smooth functions and associated variational problems. Comm. Pure Appl. Math. 42(5), 577–685 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  28. Nimbarte, N.M., Mushrif, M.M.: Multi-level thresholding algorithm for color image segmentation. In: 2010 Second International Conference on Computer Engineering and Applications (ICCEA), pp. 231–233. IEEE (2010)

    Google Scholar 

  29. Ohashi, T., Aghbari, Z., Makinouchi, A.: Hill-climbing algorithm for efficient color-based image segmentation. In: IASTED International Conference on Signal Processing, Pattern Recognition, and Applications, pp. 17–22 (2003)

    Google Scholar 

  30. Otsu, N.: A threshold selection method from gray-level histograms. Automatica 11(285-296), 23–27 (1975)

    Google Scholar 

  31. Singh, M., Patel, P., Khosla, D., Kim, T.: Segmentation of functional mri by k-means clustering. IEEE Transactions on Nuclear Science 43(3), 2030–2036 (1996)

    Article  Google Scholar 

  32. Sochen, N., Kimmel, R., Malladi, R.: A general framework for low level vision. IEEE Transactions on Image Processing 7(3), 310–318 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  33. Storath, M., Weinmann, A.: Fast partitioning of vector-valued images. SIAM Journal on Imaging Sciences 7(3), 1826–1852 (2014)

    Article  MathSciNet  Google Scholar 

  34. Vese, L.A., Chan, T.F.: A multiphase level set framework for image segmentation using the mumford and shah model. International Journal of Computer Vision 50(3), 271–293 (2002)

    Article  MATH  Google Scholar 

  35. Weber, A.: The usc-sipi image database. Signal and Image Processing Institute of the University of Southern California (1997), http://sipi.usc.edu/services/database

  36. Yuan, J., Bae, E., Tai, X.C.: A study on continuous max-flow and min-cut approaches. In: 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2217–2224. IEEE (2010)

    Google Scholar 

  37. Yuan, J., Bae, E., Tai, X.-C., Boykov, Y.: A continuous max-flow approach to potts model. In: Daniilidis, K., Maragos, P., Paragios, N. (eds.) ECCV 2010, Part VI. LNCS, vol. 6316, pp. 379–392. Springer, Heidelberg (2010)

    Chapter  Google Scholar 

  38. Zhang, R., Bresson, X., Chan, T.F., Tai, X.C.: Four color theorem and convex relaxation for image segmentation with any number of regions. Inverse Problems and Imaging 7(3), 1099–1113 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  39. Zhu, W., Tai, X.C., Chan, T.: Augmented lagrangian method for a mean curvature based image denoising model. Inverse Problems and Imaging 7(4), 1409–1432 (2013)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Hong Kong Baptist University, Hong Kong, China

    Zhi Li & Tieyong Zeng

Authors
  1. Zhi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tieyong Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Mathematics, University of Bergen, 7800, Bergen, Norway

    Xue-Cheng Tai

  2. Department of Mathematics, University of California, Los Angeles, CA, USA

    Egil Bae

  3. The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, S.A.R.

    Tony F. Chan

  4. Telemark University College, Postboks 203, 3901, Porsgrunn, Norway

    Marius Lysaker

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer International Publishing Switzerland

About this paper

Cite this paper

Li, Z., Zeng, T. (2015). Color Image Segmentation by Minimal Surface Smoothing. In: Tai, XC., Bae, E., Chan, T.F., Lysaker, M. (eds) Energy Minimization Methods in Computer Vision and Pattern Recognition. EMMCVPR 2015. Lecture Notes in Computer Science, vol 8932. Springer, Cham. https://doi.org/10.1007/978-3-319-14612-6_24

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-14612-6_24

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-14611-9

  • Online ISBN: 978-3-319-14612-6

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics