Abstract
Dominion is a complex game, with hidden information and stochastic elements. This makes creating any artificial intelligence (AI) challenging. To this date, there is little work in the literature on AI for Dominion, and existing solutions rely upon carefully tuned finite-state solutions.
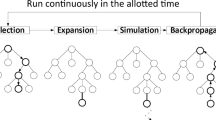
This paper presents two novel AIs for Dominion based on Monte-Carlo Tree Search (MCTS) methods. This is achieved by employing Upper Confidence Bounds (UCB) and Upper Confidence Bounds applied to Trees (UCT). The proposed solutions are notably better than existing work. The strongest proposal is able to win 67% of games played against a known, good finite-state solution, even when the finite-state solution has the unfair advantage of starting the game.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Jansen, J.V., Tollisen, R.: An ai for dominion based on monte-carlo methods (2014)
Fynbo, R.B., Nellemann, C.: Developing an agent for dominion using modern ai-approaches. Master’s thesis, IT University of Copenhagen (2010)
Fisher, M.: Provincial: A kingdom-adaptive ai for dominion (2014)
Chaslot, G.: Monte-Carlo Tree Search. PhD thesis, Maastricht University (2010)
Kocsis, L., Szepesvári, C.: Bandit based monte-carlo planning. In: Fürnkranz, J., Scheffer, T., Spiliopoulou, M. (eds.) ECML 2006. LNCS (LNAI), vol. 4212, pp. 282–293. Springer, Heidelberg (2006)
Auer, P., Cesa-Bianchi, N., Fischer, P.: Finite-time analysis of the multiarmed bandit problem. Machine learning 47(2–3), 235–256 (2002)
Gelly, S., Wang, Y.: Exploration exploitation in go: Uct for monte-carlo go (2006)
Auer, P., Ortner, R.: Ucb revisited: Improved regret bounds for the stochastic multi-armed bandit problem. Periodica Mathematica Hungarica 61(1–2), 55–65 (2010)
Coquelin, P.A., Munos, R.: Bandit algorithms for tree search (2007). arXiv preprint cs/0703062
Gelly, S., Silver, D.: Monte-carlo tree search and rapid action value estimation in computer go. Artificial Intelligence 175(11), 1856–1875 (2011)
Wizards of the Coast. Magic: The Gathering (2013). http://www.wizards.com/Magic/Summoner/ (visited on 05/30/2014)
GmbH, C.: The official website for the settlers of catan (2014)
Ward, C.D., Cowling, P.I.: Monte carlo search applied to card selection in magic: the gathering. In: IEEE Symposium on Computational Intelligence and Games, CIG 2009, pp. 9–16. IEEE (2009)
Cowling, P.I., Ward, C.D., Powley, E.J.: Ensemble determinization in monte carlo tree search for the imperfect information card game magic: The gathering. IEEE Transactions on Computational Intelligence and AI in Games 4(4), 241–257 (2012)
Szita, I., Chaslot, G., Spronck, P.: Monte-carlo tree search in settlers of catan. In: van den Herik, H.J., Spronck, P. (eds.) ACG 2009. LNCS, vol. 6048, pp. 21–32. Springer, Heidelberg (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Tollisen, R., Jansen, J.V., Goodwin, M., Glimsdal, S. (2015). AIs for Dominion Using Monte-Carlo Tree Search. In: Ali, M., Kwon, Y., Lee, CH., Kim, J., Kim, Y. (eds) Current Approaches in Applied Artificial Intelligence. IEA/AIE 2015. Lecture Notes in Computer Science(), vol 9101. Springer, Cham. https://doi.org/10.1007/978-3-319-19066-2_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-19066-2_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-19065-5
Online ISBN: 978-3-319-19066-2
eBook Packages: Computer ScienceComputer Science (R0)