Abstract
In this paper, we investigate the microscopic social mechanisms through agent-based modeling and empirical data analysis with the aim to detect the intrinsic link between local structure balance and global pattern. The investigation based on Hopfield model suggest that three types of social influences give rise to the emergence of macroscopic polarization, and the polarization pattern is closely linked with local structure balance. In addition, the corresponding empirical examples are provided to verify the social mechanisms and model simulation results.
Similar content being viewed by others
Keywords
- Social influences
- Agents-based modeling
- Empirical data analysis
- Structure balance
- Macroscopic polarization
1 Introduction
Global polarization is widely observed in human society. Examples about the group behaviors patterns include culture, social norms, political election, and online public debates on highlighted issues. In politics, polarization refers to the divergence of political attitudes to ideological extremes. Polarization can refer to such divergence in public opinion as a whole, or to such divergence within a particular subset or subgroup. Polarization as one of the interesting social phenomena is widely studied in many fields, such as social science, economics, and mass communication.
The implications of group polarization are not entirely clear and may include some beneficial as well as detrimental consequences. From decision-making perspective, the global pattern of collective dynamics is rooted from individuals’ micro-level decision-making processes, where social influence as one of the important social psychological factors, plays a dominant role. Generally to say, from the social influence point of view, three types of impact run through the whole processes of group decision-making especially in voting. One is positive influence among in-group members; this kind of social force accelerates intra-group opinion convergence. The second one is the negative social impact which may block the formation of consensus among different groups. The third type refers one kind of special individuals’ attitudes, or a state that the individuals do not belong to any labeled subgroups; members in the group have no common social identity, no firm stand about some opinions and are in a state of neither fish nor fowl [10–12].
From a bottom-up point of view, in modeling social processes, individuals’ local cumulative interacting behaviors would evolve into different global patterns. The emergence of global features comes from the local interconnecting mechanism, e.g., short average path and high clustering coefficients contribute to small world mechanism [17]. However, it is difficult to infer how the global patterns are generated from certain simple local aggregated social processes. In such cases, agent-based simulation technique is a useful tool. The goal of agent-based modeling is to enrich our understanding of fundamental processes that may appear in a variety of applications. This methodology is useful as demonstrated by Reynolds [16] when he modeled the movement of a population of artificial “boids” based on three simple rules:
-
Separation: Do not get too close to any object, including other boids.
-
Alignment: Try to match the speed and direction of nearby boids.
-
Cohesion: Head for the perceived center of mass of the boids in your immediate neighborhood.
From then on, agent-based models of human social interaction based on this same theory-building strategy are becoming acceptable potential and powerful tools for sociologists. Recent developments demonstrate how this technique can provide sociologists with a more rigorous method for specifying the micro foundations of global patterns at the relational level. For example, agent-based models (ABMs) can show how simple and predictable local interactions can generate familiar but enigmatic global patterns, such as the diffusion of information, emergence of norms, coordination of conventions, or participation in collective action [15].
In this study, as well as in its earlier version [13], agent-based modeling is used to investigate how social influences lead to group polarization and the intrinsic link which forms local influence structure balance with the emergence of global bipolarization pattern. Besides we use online empirical data analysis to verify the simulation conclusion.
The rest of the paper is organized as follows: in Sect. 2 we present global balance index (GBI). In Sect. 3 we examine the relationship between social influence and bipolarization through Hopfield attractor model (HAM), especially we focus on the connection between global polarization pattern and triad balance at the micro-level. In Sect. 4 we use empirical data analysis results to show that HAM makes sense to explain the real-world phenomenon. Section 5 presents our concluding remarks.
2 Global Balance Index and Local Structure Balance
Social balance theory provides us an interesting theoretical base to analyze how a social group evolves to the possible balance state. In this study, we investigate how influence signs (\( - 1,\,+1,\,0 \)) change at the dyadic level affects the global (collective) balance state in the whole interpersonal network.
It is assumed that the interpersonal network tends toward higher balance [8], or to be evolved with the probabilities as shown in Eq. (1)
Next we introduce the global balance index (GBI), with the aim of application to measure group voting polar patterns for Hopfield network simulation. Given a signed network, a fundamental problem is how to construct a dynamics of sign changes on the edges such that asymptotically the entire network is found on a perfectly balanced state. We use the GBI defined in [6] Eq. (2) to measure the network global balance level.
where the summation runs over all adjacent pairs of nodes, \( s_{i} \in \{ \pm 1\} \), \( i = 1, \ldots ,n \) represents agent \( i\prime \) s opinion, and R ij represents the social influence which can be positive, negative and neutral, i.e., \( R_{ij} \in \{ +1,\, -1,\,0\} \).
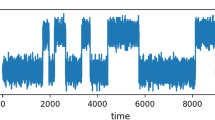
Computing global balance means assigning “+1” or “−1” to each node in the network so as to minimize the GBI. GBI approximates to 0 means that interpersonal network reaches a global structure balance state. We randomly generate a 10 × 10 interpersonal network and 1 × 10 opinion vector. Figure 1 shows the dynamic signed influence network balance processes with using GBI as one measure, we simulate 10 times and observe that each time the GBI reaches 0, i.e., the social network reaches a global network balance state within 1200 steps.
Globally, after the interpersonal network reaches stable balance level, we detect the local triadic interpersonal structure by using R package sna [2]. Figure 2 illustrates that code 300 is the only triadic structure remained, which according to [8] suggests that when GBI = 0, local interpersonal relation attains structure stable state.
Next we illustrate the local structure balance and global polarization pattern using the Hopfield attractor model by considering the dyadic ties.
3 Hopfield Attractor Model with Dyadic Influence Ties
3.1 The Hopfield Attractor Model
Macy et al. [14] presented a Hopfield model to describe group polarization problems, with considering individual decision-making dimensions, social ties signs, strengths, culture dissemination theories, etc. The modeling mechanism is as follows. The cumulative social pressure of each individual \( i \) to choose one opinion \( s_{\text{i}} \) is denoted as in Eq. (3),
where \( s_{\text{i}} = \pm 1 \) represents binary voting opinions, \( N \) is group size, \( I_{ij} \) is the weight of the social ties that individual \( j\,(j \ne i) \) connect to \( i \), and the matrix \( I \) is termed social influence matrix.
Comparing with Macy et al. [14], with the motivation of investigating the relationship between non-positive social influence and group opinions polarization, instead assigning continuous values between \( - 1 \) and \( + 1 \) to social ties \( I_{ij} \), we assign three discrete values \( - 1, + 1 \,{\text{and}}\, 0 \) to \( I_{\text{ij}} \) to indicate the three types of dyadic social influence as defined in [10–12]. Furthermore, by considering the external intervention \( X_{\text{i}} ( - 0.5 \le X_{\text{i}} \le 0.5) \), i.e., the influence to the individual’s opinion comes from other out-group’s impact; the cumulative social pressure is computed by Eq. (4).
where \( v_{\text{s}} (0 \le v_{\text{s}} \le 1) \) is used to trade off the internal and external group influence to the individual \( i ' {\text{s}} \) opinion, and K is the size of opinions dimension. Given a randomly selected threshold \( \uppi(0 < \pi < 1) \), if \( \uptau_{\text{is}} \ge\uppi \), individual \( i \) chooses +1 (support), else chooses −1 (oppose). Equation (5) describes the update of influence processes of individual \( j \) to \( i \) \( (j \ne i) \),
where \( t \) is the time step, \( \upalpha \) is an adjustable parameter between 0 and 1. Based the Hopfield attractor model, [12] extended the dyadic influence structure to triadic scenarios. They also discussed the intrinsic connection between local dyadic and triadic structures balance and global bipolarization pattern.
Next we illustrate the local structure balance and global polarization pattern using the Hopfield attractor model by considering the dyadic ties.
3.2 Analysis of Simulation Results
We take the test by setting \( N = 20 \), \( K = 5 \), \( \uppi \) belong to [0, 1] uniform distribution and \( \upalpha = 0.5 \). We run 100 times for average. Figure 3a shows the group initial random opinions states when each agent \( i \) faces \( K \) dimension decision making (before self-organizing polarization). Figure 3b illustrates the group bipolarization state under the condition of no external influence (\( v_{\text{s}} = 1 \)) and with three types of influence. We can observe that two patterns appear after group polarization, i.e., one pattern is (−1, −1, −1, −1, −1), i.e., (black, black, black, black, black) (marked by \( v_{1} \)), the other is (+1, +1, +1, +1, +1), i.e., (white, white, white, white, white) (represented by \( v_{2} \)). The ratio of the 2-pattern size approximates to 1:1.
The relationship between exogenous intervention parameter \( v_{\text{s}} \) to group polarization is as shown in Fig. 4. We see that when \( v_{\text{s}} = 1 \) (no external intervention to the group interaction processes), the ratio of is \( v_{1} /(v_{1} + v_{2} ) \) approximate to 0.5. However, the fifty to fifty well-matched equilibrium will be destroyed with a little cut off \( v_{\text{s}} \). In other words, external intervention will lead to the majority pattern. In particular, when \( v_{\text{s}} = 0.5 \), i.e., group opinion is evenly affected by external and internal factors, we observe the group consensus appears, i.e., \( v_{1} /(v_{1} + v_{2} ) \) approximates to 1, the pattern \( v_{2 } \) nearly disappears. It is clearly suggested that, under the condition of imposing external intervention, the group reaches majority or consensus pattern. With no exogenous impact, the group evolves into bipolarization state in the end. We also simulate the case with no negative social influence. The modeling result shows that under the condition with no external intervention, the group reaches the majority or consensus pattern. The result might conclude that non-positive social influence promotes group opinion bipolarization, which is consistent with our previous conclusion in [12]. Furthermore, we investigate the triadic relation motifs distribution before and after bipolarization by using R package sna [2]. We find that the overwhelming structure balanceFootnote 1 motifs emerge concurrently with polarization process.
Exogenous intervention impact on group polarization (In Eq. (4), we adjust vs from 1 to 0.5, i.e., increasing the out-group intervention from 0 to 0.5, by which we observe impact of the exogenous intervention on group opinions polarization)
Figure 5 presents the dynamic variation of triadic distributions. The upper plot in Fig. 5 shows the initial local triads distribution as t = 0 according to randomly generated social influence matrix. We can observe that all 16 types of triads exist in the initial triadic relationships. With the social influence matrix updating, at step \( t = 19 \) some triad motifs disappear, e.g., Code 003, Code 012, and Code 102, while Code 300, Code 210 become dominant (see middle plot in Fig. 5). Finally, at step \( t = 29 \), other triad motifs disappear except balanced triad motif Code 300 (as shown in the bottom plot of Fig. 5), which means that GBI = 0 and the group achieves the stable state.
The simulation results of Hopfield attractor model suggest that non-positive social influence promotes group bipolarization pattern. In addition, HAM simulation result concludes that opinions polarization in a group is coexisted with local level structure balance, which reveals some interesting internal connection between global collective pattern and local social structure stability.
4 The Evidences from Real World
In this section, we present two empirical illustrations. One shows that non-positive influence as one important factor that promotes voters’ opinions polarization. Another suggests that online social network demonstrates the local structure stable characteristic.
4.1 Political Polarization on Twitter
Social media play an important role in shaping political discourse in the US and around the world. Some empirical evidences reveal that politically active Web 2.0 enabled social media users tend to organize into insular, homogenous communities segregated along partisan lines. For example, Adamic and Glance [1] demonstrated that political blogs preferentially linked to other blogs of the same political ideology. Their finding is also supported by Hargittai et al. [7], which shows that Internet users who share same political point of view tend to behave similarly, such as choose to read blogs that share their political beliefs.
More insightful evidences came from Conover et al. [4] who studied some networks of political communication on the Twitter microblogging service during the 6 weeks prior to the 2010 US midterm elections. That study shows that the retweet network exhibits a highly modular structure, segregating users into two homogeneous communities corresponding to the political left and right, which demonstrate the obvious bipolarization characteristic. A surprising contrast is that the mention network does not exhibit this kind of political polarization pattern, resulting in users being exposed to individuals and information they would not have been likely to choose in advance. Figure 6 displays this kind of group opinions dynamic pattern.
The political retweet (left) and mention (right) networks. The color of node reflects cluster assignments. Community structure is evident in the retweet network, but less so in the mention network. In the retweet network, the red cluster A is made of 93 % right-leaning users, while the blue cluster B is made of 80 % left-leaning users [4]
Their findings suggest that the possibility that in–group/out-group differentiation and rejection antagonism, or the non-positive social influence between intra-group members and intergroup members is the emergent cause of social network self-organization, and leads to the bipolarization global dynamic pattern.
4.2 Local Structure Balance on the Trust Network of Epinions
In this section, we will detect the local structure balance among mixed relationships, i.e., positive, negative, and neutral. We use the trust network constructed with the product reviews in the Epinions Web site, where people can not only indicate their trust, distrust, or no comments of the reviews of others, but also give both positive and negative ratings either to items or to the other raters. In our study, we analyze the Epinions dataset with 131828 nodes and 841372 edges. The basic statistics about Epinions data set is as listed in Table 1.
In Table 1, “+Δ” stands for the triadic relationship that satisfies structure balance, “−Δ” denotes for the unbalance triadic relation. “+Edges” stands for the trust relationship, “−Edges” denotes for the opposite. Figure 7 shows that most of the edges are embedded into smaller size community (subgroup), and only a few edges are embedded into high density modular structure. However, it is worth noting that in both scenarios the balanced triads distribution is higher than that of the unbalanced counterparts.
We also analyze the 16 types triads distribution for three cases, trust or positive “+,” distrust or non-positive “−,” mixed or including three scenarios no comments relationships by “0,” and “+,” “−,” correspondingly. Our findings are that the size of local triadic balance structure such as 16-#300, 3-#102, 11-#201 in the network constructed by trust edges (or positive “+” relationship) and mixed relationship (including “+,” “0,” and “−” links) is more than that in the distrust (or negative “−” relationship) network, as shown in Fig. 8. These observations fit well into Heider’s original notion of structural balance, which in its strongest form postulates that when considering the relationships between three people, either only one or all three of the relations should be positive.
5 Conclusions
In this paper, we have investigated the non-positive social impact on group polarization based on agent-based modeling and real-world data analysis. By simulation we find that bipolarization pattern tends to emerge with no external intervention, and consensus may occur among group members if the non-positive influence is neglected.
With dyadic influence considered, by HAM simulation we observe that dyadic influence balance among agents has inherent relation with global bipolarization pattern. This is similar to the macro--micro linkage: sentiment relations among agents (localized as triad and dyad) lead to the collective balance of the group.
Two empirical evidences are consistent with our modeling results. The bipolarization on Twitter shows that no-positive influence as an important factor promotes voters’ opinions polarization, while Epinions’ trust network demonstrates the local structure stable characteristic existed in the online signed social network. Those data analyzing results are closely connected to the theories of classic social psychology and structure balance which tend to capture certain common patterns of interaction.
Why are some communities, organizations, and social group characterized by cooperation, trust, and solidarity, i.e., consensus pattern, whereas others are fraught with corruption, discord, and fear, i.e., unconformity or polarization pattern? We argue that viewed from the bottom up, the answer centers on global pattern that has its micro-level social mechanisms. By these underlying principles, decision making is distributed and global order self-organizes out of multiplex local interactions among autonomous interdependent actors.
Notes
- 1.
Holland and Leinhardt [9] addressed that classic balance theory offers a set of simple local rules for relational change and classified local triadic motifs into 16 types, according to mutual reciprocity, asymmetry relation and non-relationship between pairs (or dyadic relations), where Code 300 triad relation corresponding to structure balance under the condition of the triad product signs satisfies “+”. More details about structure balance refer to [3, 5, 8, 9].
References
Adamic, L., Glance, N.: The political blogosphere and the 2004 U.S. election: divided they blog. In: Proceedings of 3rd International Workshop on Link Discovery (LinkKDD 2005), pp. 36–43 (2005)
Butts, C.T.: Social network analysis with SNA. J. Stat. Softw. 24(6), 1–51 (2008)
Cartwright, D., Harary, F.: Structural balance: a generalization of Heider’s theory. Psychol. Rev. 63, 277–292 (1956)
Conover, M.D., Ratkiewicz, J., Francisco, M., Goncalves, B., Flammini, A., Menczer, F.: Political polarization on twitter. In: Proceedings of the 5th International Conference on Weblogs and Social Media 2011, Barcelona, Spain, pp. 237–288 (2011)
Davis, J.A., Leinhardt, S.: The structure of positive interpersonal relations in small groups. In: Berger, J. (ed.) Sociological Theories in Progress, vol. 2, pp. 218–251. Houghton Mifflin, Boston (1972)
Facchetti, G., Iacono, G., Altafini, C.: Computing global structural balance in large-scale signed social networks. PNAS 108(52), 20953–20958 (2011)
Hargittai, E., Gallo, J., Kane, M.: Cross ideological discussions among conservative and liberal bloggers. Public Choice 134(1), 67–86 (2007)
Heider, F.: Attitudes and cognitive organization. J. Psychol. 21, 107–112 (1946)
Holland, P.W., Leinhardt, S.: A method for detecting structure in sociometric data. Am. J. Sociol. 70, 492–513 (1970)
Li, Z.P., Tang, X.J.: Group polarization and non-positive social influence: a revised voter model study. In: Hu, B., Liu, J., Chen, L., Zhong, N. (eds.) Brain Informatics—International Conference, BI 2011, Lanzhou, China, September 7–9, 2011. In: Proceedings Lecture Notes in Computer Science, vol. 6889, pp. 295-303. Springer, Berlin (2011)
Li, Z.P., Tang, X.J.: Polarization and non-positive social influence: a hopfield model of emergent structure. Int. J. Knowl. Syst. Sci. 3(3), 15–25 (2012)
Li, Z.P., Tang, X.J.: Group polarization: connecting, influence and balance, a simulation study based on hopfield modeling. In: PRICAI 2012, pp. 710-721 (2012)
Li, Z.P., Tang, X.J.: Modeling and empirical investigation on the microscopic social structure and global group pattern. In: Skulimowski A.M.J. (ed.) Looking into the Future of Creativity and Decision Support Systems: In: Proceedings of the 8th International Conference on Knowledge, Information and Creativity Support Systems, Kraków, Poland, 7–9 Nov 2013. Advances in decision sciences and future studies, vol. 2, pp. 339–349. Progress & Business Publishers, Kraków (2013)
Macy, M.W., Kitts, J.A., Flache, A.: Polarization in dynamic networks a hopfield model of emergent structure. In: Breiger, R., Carley, K., Pattison, P. (eds.) Dynamic Social Network Modeling and Analysis: Workshop Summary and Papers, pp. 162–173. The National Academies Press, Washington DC (2003)
Macy, M.W., Willer, R.: From factors to actors: computational sociology and agent-based modeling. Ann. Rev. Sociol. 28, 143–166 (2002)
Reynolds, C.W.: Flocks, herds and schools: a distributed behavioral model. In: ACM SIGGRAPH Computer Graphics ACM 1987, 21(4), pp. 25–34 (1987)
Watts, D.J., Strogatz, S.: Collective dynamics of “small-world” networks. Nature 393(6684), 440–442 (1998)
Acknowledgments
This research is supported by National Basic Research Program of China under Grant No. 2010CB731405, National Natural Science Foundation of China under Grant No. 71171187, and Research Fund of Dali University (No. KYBKY1219210110).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Li, Z., Tang, X. (2016). Modeling and Empirical Investigation on the Microscopic Social Structure and Global Group Pattern. In: Skulimowski, A., Kacprzyk, J. (eds) Knowledge, Information and Creativity Support Systems: Recent Trends, Advances and Solutions. Advances in Intelligent Systems and Computing, vol 364. Springer, Cham. https://doi.org/10.1007/978-3-319-19090-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-19090-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-19089-1
Online ISBN: 978-3-319-19090-7
eBook Packages: Computer ScienceComputer Science (R0)