Abstract
We provide a hierarchy of tree languages recognised by nondeterministic parity tree automata with priorities in \(\{0,1,2\}\), whose length exceeds the first fixed point of the \(\varepsilon \) operation (that itself enumerates the fixed points of \(x\mapsto \omega ^x\)). We conjecture that, up to Wadge equivalence, it exhibits all regular tree languages of index \([0,2]\).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
We emphasize that this is done without any determinacy principle. In particular, we do not require \(\mathbf {\Delta }^{1}_{2}\)-determinacy.
- 2.
Not to be mistaken with an \(\varepsilon \)-move.
- 3.
A pointclass is a collections of subsets of a topological space that is closed under continuous preimages.
- 4.
This is in general stronger than the usual \(A<_{W}B\) if and only if \(A\le _{W}B\) and \(B\not \le _{W}A\), but the two definitions coincide when the classes considered are determined.
- 5.
A player in charge of
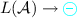 in a conciliatory game is like a player in charge of \(L(\mathcal {A})\), but with the extra possibility at any moment of the play to reach a definitively rejecting position.
in a conciliatory game is like a player in charge of \(L(\mathcal {A})\), but with the extra possibility at any moment of the play to reach a definitively rejecting position. - 6.
\( \varepsilon = {\left\{ \begin{array}{ll} -1 &{}\text { if } d_{c}(L)<\omega ; \\ 0 &{}\text { if } d_{c}(L) = \beta + n \text { and } {{\mathrm{cof}}}(\beta ) = \omega _{1}; \\ 1 &{}\text { if } d_{c}(L) = \beta + n \text { and } {{\mathrm{cof}}}(\beta ) = \omega . \end{array}\right. } \).
- 7.
Another way to characterise \(\varphi _{2}(0)\) is to remember that an ordinal is the set of its predecessors and notice that a nonzero ordinal is of the form respectively \(\omega ^\alpha \) iff it is closed under addition and \(\varepsilon _\alpha \) iff it is closed under \(x\longmapsto \omega ^x\). Then \(\varphi _{2}(0)\) is the first non null ordinal closed under \(x\longmapsto \varepsilon _x\) as well as \(x\longmapsto \omega ^x\) and \(x,y\longmapsto x+y\).
- 8.
Notice that we have \({\alpha _i}={\left( \omega ^{\omega }\right) }^{\alpha _i}\iff {\alpha _i}={\omega ^{\alpha _i}}\).
References
Andretta, A., Louveau, A.: Wadge degrees and pointclasses. In: Kechris, A.S., Löwe, B., Steel, J.R. (eds.) Wadge Degrees and Projective Ordinals: The Cabal Seminar, vol. II, pp. 3–23. Cambridge University Press, Cambridge (2012)
Arnold, A., Duparc, J., Murlak, F., Niwiński, D.: On the topological complexity of tree languages. Logic Automata: Hist. Perspect. 2, 9–29 (2007)
Arnold, A., Niwiński, D.: Rudiments of \(\mu \)-Calculus. Studies in Logic and the Foundations of Mathematics. Elseiver, Amsterdam (2001)
Duparc, J.: Wadge hierarchy and Veblen hierarchy, part I: Borel sets of finite rank. J. Symbolic Logic 66(1), 56–86 (2001)
Duparc, J., Murlak, F.: On the topological complexity of weakly recognizable tree languages. In: Csuhaj-Varjú, E., Ésik, Z. (eds.) FCT 2007. LNCS, vol. 4639, pp. 261–273. Springer, Heidelberg (2007)
Finkel, O., Simonnet, P.: On recognizable tree languages beyond the Borel hierarchy. Fundam. Informaticae 95(2–3), 287–303 (2009)
Rabin, M.O.: Decidability of second-order theories and automata on infinite trees. Trans. AMS 141, 1–23 (1969)
Van Wesep, R.: Wadge degrees and descriptive set theory. In: Kechris, A.S., Moschovakis, Y.N. (eds.) Cabal Seminar 76–77, pp. 151–170. Springer, Heidelberg (1978)
Wadge, W.W.: Reducibility and determinateness on the Baire space. Ph.D. thesis, University of California, Berkeley (1984)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Duparc, J., Fournier, K. (2015). A Tentative Approach for the Wadge-Wagner Hierarchy of Regular Tree Languages of Index [0, 2]. In: Shallit, J., Okhotin, A. (eds) Descriptional Complexity of Formal Systems. DCFS 2015. Lecture Notes in Computer Science(), vol 9118. Springer, Cham. https://doi.org/10.1007/978-3-319-19225-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-19225-3_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-19224-6
Online ISBN: 978-3-319-19225-3
eBook Packages: Computer ScienceComputer Science (R0)





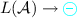 in a conciliatory game is like a player in charge of
in a conciliatory game is like a player in charge of