Abstract
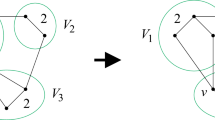
Computing maximum independent sets in graphs is an important problem in computer science. In this paper, we develop an evolutionary algorithm to tackle the problem. The core innovations of the algorithm are very natural combine operations based on graph partitioning and local search algorithms. More precisely, we employ a state-of-the-art graph partitioner to derive operations that enable us to quickly exchange whole blocks of given independent sets. To enhance newly computed offsprings we combine our operators with a local search algorithm. Our experimental evaluation indicates that we are able to outperform state-of-the-art algorithms on a variety of instances.
Graph Partitioning for Independent Sets—Partially supported by DFG Gottfried Wilhelm Leibniz Prize 2012 for Peter Sanders.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Andrade, D.V., Resende, M.G.C., Werneck, R.F.: Fast Local Search for the Maximum Independent Set Problem. J. Heuristics 18(4), 525–547 (2012)
Bäck, T.: Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms. Ph.D thesis (1996)
Bäck, T., Khuri, S.: An evolutionary heuristic for the maximum independent set problem. In: Proc. 1st IEEE Conf. on Evolutionary Computation, pp. 531–535. IEEE (1994)
Bader, D., Kappes, A., Meyerhenke, H., Sanders, P., Schulz, C., Wagner, D.: Benchmarking for graph clustering and partitioning. In: Encyclopedia of Social Network Analysis and Mining. Springer (2014)
Battiti, R., Protasi, M.: Reactive Local Search for the Maximum Clique Problem. Algorithmica 29(4), 610–637 (2001)
Borisovsky, P.A., Zavolovskaya, M.S.: Experimental comparison of two evolutionary algorithms for the independent set problem. In: Raidl, G.R., Cagnoni, S., Cardalda, J.J.R., Corne, D.W., Gottlieb, J., Guillot, A., Hart, E., Johnson, C.G., Marchiori, E., Meyer, J.-A., Middendorf, M. (eds.) EvoIASP 2003, EvoWorkshops 2003, EvoSTIM 2003, EvoROB/EvoRobot 2003, EvoCOP 2003, EvoBIO 2003, and EvoMUSART 2003. LNCS, vol. 2611, pp. 154–164. Springer, Heidelberg (2003)
Davis, T.: The University of Florida Sparse Matrix Collection
De Jong, K.A.: Evolutionary Computation: A Unified Approach. MIT Press (2006)
Feo, T.A., Resende, M.G.C., Smith, S.H.: A Greedy Randomized Adaptive Search Procedure for Maximum Independent Set. Operations Research 42(5), 860–878 (1994)
Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman (1979)
Gemsa, A., Niedermann, B., Nöllenburg, M.: Trajectory-based dynamic map labeling. In: Cai, L., Cheng, S.-W., Lam, T.-W. (eds.) Algorithms and Computation. LNCS, vol. 8283, pp. 413–423. Springer, Heidelberg (2013)
Goldberg, D.E.: Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley (1989)
Grosso, A., Locatelli, M., Della Croce, F.: Combining Swaps and Node Weights in an Adaptive Greedy Approach for the Maximum Clique Problem. J. Heuristics 10(2), 135–152 (2004)
Grosso, A., Locatelli, M., Pullan, W.: Simple Ingredients Leading to Very Efficient Heuristics for the Maximum Clique Problem. J. Heuristics 14(6), 587–612 (2008)
Hansen, P., Mladenović, N., Urošević, D.: Variable Neighborhood Search for the Maximum Clique. Discrete Applied Mathematics 145(1), 117–125 (2004)
Katayama, K., Hamamoto, A., Narihisa, H.: An Effective Local Search for the Maximum Clique Problem. Inf. Proc. Letters 95(5), 503–511 (2005)
Lamm, S.: Evolutionary Algorithms for Independent Sets. Bachelor’s Thesis, KIT (2014)
Lamm, S., Sanders, P., Schulz, C.: Graph Partitioning for Independent Sets. Technical Report arxiv:1502.01687 (2015)
Meyerhenke, H., Sanders, P., Schulz, C.: Partitioning complex networks via size-constrained clustering. In: Gudmundsson, J., Katajainen, J. (eds.) SEA 2014. LNCS, vol. 8504, pp. 351–363. Springer, Heidelberg (2014)
Miller, B.L., Goldberg, D.E.: Genetic Algorithms, Tournament Selection, and the Effects of Noise. Evolutionary Computation 4(2), 113–131 (1996)
Pullan, W.J., Hoos, H.H.: Dynamic Local Search for the Maximum Clique Problem. J. Artif. Intell. Res. (JAIR) 25, 159–185 (2006)
Sanders, P., Schulz, C.: KaHIP - Karlsruhe High Qualtity Partitioning Homepage. http://algo2.iti.kit.edu/documents/kahip/index.html
Sanders, P., Schulz, C.: Think locally, act globally: highly balanced graph partitioning. In: Demetrescu, C., Marchetti-Spaccamela, A., Bonifaci, V. (eds.) SEA 2013. LNCS, vol. 7933, pp. 164–175. Springer, Heidelberg (2013)
Soper, A.J., Walshaw, C., Cross, M.: A Combined Evolutionary Search and Multilevel Optimisation Approach to Graph-Partitioning. J. of Global Optimization 29(2), 225–241 (2004)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Lamm, S., Sanders, P., Schulz, C. (2015). Graph Partitioning for Independent Sets. In: Bampis, E. (eds) Experimental Algorithms. SEA 2015. Lecture Notes in Computer Science(), vol 9125. Springer, Cham. https://doi.org/10.1007/978-3-319-20086-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-20086-6_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-20085-9
Online ISBN: 978-3-319-20086-6
eBook Packages: Computer ScienceComputer Science (R0)