A Robust Clustering via Swarm Intelligence

Abstract

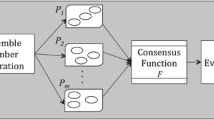
A very promising approach to reach a robust partitioning is to use ensemble-based learning. In this way, the classification/clustering task is more reliable, because the classifiers/clusterers in the ensemble cover the faults of each other. The common policy in clustering ensemble based learning is to generate a set of primary partitionings that are different from each other. These primary partitionings could be generated by a clustering algorithm with different initializations. It is popular to filter some of these primary partitionings, i.e. a subset of the produced partitionings is selected for the final ensemble. The selection phase is done to reach a diverse ensemble. A consensus function finally aggregates the ensemble into a final partitioning called also the consensus partitioning. Another alternative policy in the clustering ensemble based learning is to use the fusion of some primary partitionings that come from naturally different sources. On the other hand, swarm intelligence is also a new topic where the simple agents work in such a way that a complex behavior can be emerged. The necessary diversity for the ensemble can be achieved by the inherent randomness of swarm intelligence algorithms. In this paper we introduce a new clustering ensemble learning method based on the ant colony clustering algorithm. Indeed ensemble needs diversity vitally and swarm intelligence algorithms are inherently involved in randomness. Ant colony algorithms are powerful metaheuristics that use the concept of swarm intelligence. Different runnings of ant colony clustering on a dataset result in a number of diverse partitionings. Considering these results totally as a new space of the dataset we employ a final clustering by a simple partitioning algorithm to aggregate them into a consensus partitioning. From another perspective, ant colony clustering algorithms have many parameters. Effectiveness of the ant colony clustering methods is questionable because they depend on many parameters. On a test dataset, these parameters should be tuned to obtain a desirable result. But how to define them in a real task does not clear. The proposed clustering framework lets the parameters be free to be changed, and compensates non-optimality of the parameters by the ensemble power. Experimental results on some real-world datasets are presented to demonstrate the effectiveness of the proposed method in generating the final partitioning..