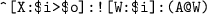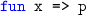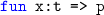Abstract
These are the lecture notes of a tutorial on higher-order modal logics held at the 11th Reasoning Web Summer School. After defining the syntax and (possible worlds) semantics of some higher-order modal logics, we show that they can be embedded into classical higher-order logic by systematically lifting the types of propositions, making them depend on a new atomic type for possible worlds. This approach allows several well-established automated and interactive reasoning tools for classical higher-order logic to be applied also to modal higher-order logic problems. Moreover, also meta reasoning about the embedded modal logics becomes possible. Finally, we illustrate how our approach can be useful for reasoning with web logics and expressive ontologies, and we also sketch a possible solution for handling inconsistent data.
C. Benzmüller—This work has been supported by the German Research Foundation DFG under grants BE2501/9-1,2 and BE2501/11-1.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
thf stands for typed higher-order form and it refers to a family of syntax formats for higher-order logic. So far only the fully developed thf0 format, for simple type theory, is in practical use.
- 2.
In thf0, which is a concrete syntax for HOL, $i and $o represent the HOL base types i and o (Booleans). $i>$o encodes a function (predicate) type. Predicate application, as in A(X, W), is encoded as ((A@X)@W) or simply as (A@X@W), i.e., function/predicate application is represented by @; universal quantification and \(\lambda \)-abstraction as in
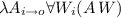 and are represented as in
and are represented as in 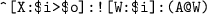
; comments begin with %.
- 3.
The 3480 problems for logic S4 can be download from http://christoph-benzmueller.de/papers/THF-S4-ALL.zip.
- 4.
See file QML.thy available at https://github.com/FormalTheology/GoedelGod/blob/master/Formalizations/Isabelle/.
- 5.
See file QML_var.thy at the github url from above.
- 6.
The keyword

indicates a lambda abstraction:
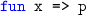
(or
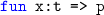
) denotes the function \(\lambda x:t.p\), which takes an argument x (of type t) and returns p.
- 7.
The underlying proof system of Coq (the Calculus of Inductive Constructions (CIC) [57]) is actually more sophisticated and minimalistic than the calculus shown in Fig. 5. But the calculus shown here suffices for the purposes of this tutorial. This calculus is classical, because of the double negation elimination rule. Although CIC is intuitionistic, it can be made classical by importing Coq’s classical library, which adds the axiom of the excluded middle and the double negation elimination lemma.
- 8.
The natural deduction calculus with the rules from Figs. 5 and 6 is sound and complete relatively to the calculus of Fig. 5 extended with a necessitation rule and the modal axiom K [67]. Starting from a sound and Henkin-complete natural deduction calculus for classical higher-order logic (cf. Fig. 5), the additional modal rules in Fig. 6 make it sound and Henkin-complete for the rigid higher-order modal logic K.
- 9.
More elegantly, we could employ an \(@_{cw}\)-operator; for example, (A6) would then be encoded as \(@_{cw} (likes Mary Bill)\) (see also Sect. 5.4).
- 10.
Fitting [36] (pp. 83ff) actually does not use a translation to higher-order logic, where worlds become part of the syntax. But what he does, using his style of syntax (which distinguishes extensional and intensional types), is essentially analogous to the translation described here.
References
Web semantics: Science, services and agents on the world wide web, special issue on reasoning with context in the semantic web, vol. 12–13, pp. 1–160 (2012)
Adams, R.M.: Introductory Note to *1970. In: Feferman, S., et al. (eds.) Kurt Gödel, Collected Works, vol. III. Oxford University Press, New York (1995)
Akman, V., Surav, M.: Steps toward formalizing context. AI Mag. 17(3), 55–72 (1996)
Alama, J., Heskes, T., Kühlwein, D., Tsivtsivadze, E., Urban, J.: Premise selection for mathematics by corpus analysis and kernel methods. J. Autom. Reasoning 52(2), 191–213 (2014)
Anderson, A.C., Gettings, M.: Gödel’s ontological proof revisited. In: Hájek, P. (ed.) Gödel ’96: Logical foundations of mathematics, computer science and physics. Lecture Notes in Logic, vol. 6, pp. 167–172. Springer, Berlin (1996)
Andrews, P.B.: General models and extensionality. J. Symb. Logic 37(2), 395–397 (1972)
Andrews, P.B.: Church’s type theory. In: Zalta, E.N. (ed.), The Stanford Encyclopedia of Philosophy. Spring 2014 edition, 2014
Andrews, P.B., Miller, D.A.: Eve Longini Cohen, and Frank Pfenning. Automating higher-order logic. In: Bledsoe, W.W., Loveland, D.W., et al., Automated Theorem Proving: After 25 Years, vol. 29 of Contemporary Mathematics series, pp. 169–192. American Mathematical Society (1984)
Andrews, P.B., Bishop, M.: On sets, types, fixed points, and checkerboards. In: Miglioli, P., Moscato, U., Mundici, D., Ornaghi, D. (eds.) Theorem Proving with Analytic Tableaux and Related Methods. LNCS, vol. 1071, pp. 1–15. Springer, Heidelberg (1996)
Marcos, J.: Modality and paraconsistency. The Logica Yearbook, pp. 213–222 (2005)
Baader, F., Calvanese, D., McGuinness, D.L., Nardi, D., Patel-Schneider, P.F. (eds.): The Description Logic Handbook: Theory, Implementation, and Applications. Cambridge University Press, New York (2003)
Benzmüller, C., Theiss, F., Paulson, L., Fietzke, A.: LEO-II - a cooperative automatic theorem prover for higher-order logic. In: Proceedings of IJCAR 2008, number 5195 in LNAI, pp. 162–170. Springer, Berlin (2008)
Benzmüller, C., Woltzenlogel Paleo, B.: Formalization, Mechanization and Automation of Gödel’s Proof of God’s Existence. arXiv: 1308.4526 (2013)
Benzmüller, C.: Verifying the modal logic cube is an easy task (for higher-order automated reasoners). In: Siegler, S., Wasser, N. (eds.) Walther Festschrift. LNCS, vol. 6463, pp. 117–128. Springer, Heidelberg (2010)
Benzmüller, C., Brown, C.: The curious inference of Boolos in MIZAR and OMEGA. In: Matuszewski, R., Zalewska, A. (eds.) From Insight to Proof - Festschrift in Honour of Andrzej Trybulec. Studies in Logic, Grammar, and Rhetoric, vol. 10(23), pp. 299–388. The University of Bialystok, Polen (2007)
Benzmüller, C., Brown, C.E., Kohlhase, M.: Higher-order semantics and extensionality. J. Symb. Logic 69(4), 1027–1088 (2004)
Benzmüller, C., Otten, J., Raths, T.: Implementing and evaluating provers for first-order modal logics. In: Raedt, L.D., Bessiere, C., Dubois, D., Doherty, P., Frasconi, P., Heintz, F., Lucas, P. (eds.), ECAI 2012, Frontiers in Artificial Intelligence and Applications, vol. 242, pp. 163–168. IOS Press, Montpellier (2012)
Benzmüller, C., Woltzenlogel Paleo, B.: Gödel’s God in Isabelle/HOL. Arch. Formal Proofs, 2013 (2013)
Benzmüller, C., Woltzenlogel Paleo, B.: Automating Gödel’s ontological proof of God’s existence with higher-order automated theorem provers. In: Schaub, T., Friedrich, G., O’Sullivan, B., (eds.), ECAI 2014, Frontiers in Artificial Intelligence and Applications, vol. 263, pp. 93–98, IOS Press (2014)
Benzmüller, C., Paulson, L.: Exploring properties of normal multimodal logics in simple type theory with LEO-II. In: Benzmüller, C., Brown, C., Siekmann, J., Statman, R. (eds.), Reasoning in Simple Type Theory – Festschrift in Honor of Peter B. Andrews on His 70th Birthday, Studies in Logic, Mathematical Logic and Foundations, pp. 386–406, College Publications (2008)
Benzmüller, C., Paulson, L.: Quantified multimodal logics in simple type theory. Logic Univers. (Spec. Issue Multimodal Logics) 7(1), 7–20 (2013)
Benzmüller, C., Pease, A.: Higher-order aspects and context in SUMO. J. Web Seman. (Spec. Issue Reasoning with context in the Semant. Web) 12–13, 104–117 (2012)
Benzmüller, Christoph, Raths, Thomas: HOL based first-order modal logic provers. In: McMillan, Ken, Middeldorp, Aart, Voronkov, Andrei (eds.) LPAR-19 2013. LNCS, vol. 8312, pp. 127–136. Springer, Heidelberg (2013)
Benzmüller, C., Weber, L., Woltzenlogel Paleo, B.: Computer-assisted analysis of the Anderson-Hájek ontological controversy. In: Silvestre, R.S., Béziau, J.-Y. (eds.), Handbook of the 1st World Congress on Logic and Religion, Joao Pessoa, Brasil (2015)
Beziau, J.Y., Carnielli, W., Gabbay, D.: Handbook of Paraconsistency. College Publications, London (2007)
Blackburn, P., van Benthem, J.F.A.K., Wolter, F.: Handbook of Modal Logic, Volume 3 (Studies in Logic and Practical Reasoning). Elsevier Science Inc., New York (2006)
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. J. Autom. Reasoning 51(1), 109–128 (2013)
Blanchette, Jasmin Christian, Nipkow, Tobias: Nitpick: A counterexample generator for higher-order logic based on a relational model finder. In: Kaufmann, Matt, Paulson, Lawrence C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 131–146. Springer, Heidelberg (2010)
Boolos, G.: A curious inference. J. Philos. Logic 16, 1–12 (1987)
Brown, C.E.: Satallax: An automated higher-order prover. In: Gramlich, B., Miller, D., Sattler, U. (eds.) Automated Reasoning. LNCS, vol. 7364, pp. 111–117. Springer, Heidelberg (2012)
Bucav, S., Buvac, V., Mason, I.A.: Metamathematics of contexts. Fundamenta Informaticae 23(3), 263–301 (1995)
Charguéraud, A.: The locally nameless representation. J. Autom. Reasoning 49(3), 363–408 (2012)
Corazzon, R.: Contemporary bibliography on ontological arguments. http://www.ontology.co/biblio/ontological-proof-contemporary-biblio.htm
da Costa, N.C.A., Alves, E.H.: Semantical analysis of the calculi cn. Notre Dame J. Formal Logic 18(4), 621–630 (1977)
Dunn, J.M., Restall, G.: Relevance logic. Handbook of Philosophical Logic 6, 1–136 (2002)
Fitting, M.: Types, Tableaux and Gödel’s God, Kluwer (2002)
Fitting, M., Mendelsohn, R.L.: First-Order Modal Logic. Synthese Library. Kluwer, Netherlands (1998)
Gabbay, D.M.: Labelled Deductive Systems. Clarendon Press, Oxford (1996)
Gallin, D.: Intensional and Higher-Order Modal Logic. North Holland, New York (1975)
Giunchiglia, F.: Contextual reasoning. Epistemologia (Special Issue on Languages and Machines) 16, 345–364 (1993)
Giunchiglia, F., Serafini, L.: Multilanguage hierarchical logics or: How we can do without modal logics. Artif. Intell. 65(1), 29–70 (1994)
Gödel, K.: Collected Works, Unpublished Essays and Letters. Ontological Proof, pp. 65–85. Oxford University Press, Oxford (1970)
Gödel, K.: Appx.A: Notes in Kurt Gödel’s Hand. In: [70], pp. 144–145 (2004)
Guha, R.V.: Context: A Formalization and Some Applications. Ph.D. thesis, Stanford University (1991)
Henkin, L.: Completeness in the theory of types. J. Symb. Logic 15(2), 81–91 (1950)
Jaśkowski, S.: Rachunek zdań dla systemów dedukcyjnych sprzecznych. Stud. Soc. Scientiarun Torunesis 1(5), 55–77 (1948)
Jaśkowski, S.: Propositional calculus for contradictory deductive systems. Stud. Logica. 24, 143–157 (1969)
Kaliszyk, C., Urban, J.: Hol(y)hammer: online ATP service for HOL light. Math. Comput. Sci. 9(1), 5–22 (2015)
Kaliszyk, C., Urban, J.: Learning-assisted theorem proving with millions of lemmas. J. Symb. Comput. 69, 109–128 (2015)
Lindblad, F.: agsyHOL website. https://github.com/frelindb/agsyHOL
McCarthy, J.: Generality in artificial intelligence. Commun. ACM 30(12), 1030–1035 (1987)
McCarthy, J.: Notes on formalizing context. In: Proceedings of IJCAI 1993, pp. 555–562 (1993)
Muskens, R.: Higher order modal logic. In: Blackburn, P., et al. (eds.) Handbook of Modal Logic, pp. 621–653. Elsevier, Dordrecht (2006)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Berlin (2002)
Otten, J.: Mleancop: A connection prover for first-order modal logic. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) Automated Reasoning. LNCS, vol. 8562, pp. 269–276. Springer, Switzerland (2014)
Woltzenlogel Paleo, B., Benzmüller, C.: Formal theology repository. (https://github.com/FormalTheology/GoedelGod)
Paulin-Mohring, C.: Introduction to the calculus of inductive constructions. In: Delahaye, D., Woltzenlogel Paleo, B. (eds.), All about Proofs, Proofs for All, Mathematical Logic and Foundations. College Publications, London (2015)
Pease, A.: Ontology: A Practical Guide. Articulate Software Press, Angwin (2011)
Pease, A., Sutcliffe, G.: First order reasoning on a large ontology. In: Sutcliffe, G., Urban, J., Schulz, S. (eds.), Proceedings of the CADE-21 Workshop on Empirically Successful Automated Reasoning in Large Theories (ESARLT), CEUR Workshop Proceedings, vol. 257, CEUR-WS.org (2007)
Priest, G.: Paraconsistent belief revision. Theoria 67, 214–228 (2001)
Priest, G., Sylvan, R.: Simplified semantics for basic relevant logics. J. Philos. Logic (1992)
Ramachandran, D., Reagan, P., Goolsbey, K.: First-orderized ResearchCyc: Expressivity and efficiency in a common-sense ontology. In: Shvaiko P. (ed.), Papers from the AAAI Workshop on Contexts and Ontologies: Theory, Practice and Applications, Pittsburgh, Pennsylvania, USA, 2005. Technical report WS-05-01 published by The AAAI Press, Menlo Park, California, July 2005
Raths, Thomas, Otten, Jens: The QMLTP problem library for first-order modal logics. In: Gramlich, Bernhard, Miller, Dale, Sattler, Uli (eds.) IJCAR 2012. LNCS, vol. 7364, pp. 454–461. Springer, Heidelberg (2012)
Restall, G., Slaney, J.: Realistic belief revision. In: Proceedings of the Second World Conference in the Fundamentals of Artificial Intelligence, pp. 367–378 (1995)
Scott, D.: Appx.B: Notes in Dana Scott’s Hand. In: [70], pp. 145–146 (2004)
Serafini, L., Bouquet, P.: Comparing formal theories of context in AI. Artif. Intell. 155, 41–67 (2004)
Siders, A., Woltzenlogel Paleo, B.: A variant of Gödel’s ontological proof in a natural deduction calculus. ( github.com/FormalTheology/GoedelGod/blob/master/Papers/InProgress/NaturalDeduction/GodProof-ND.pdf?raw=true)
Sobel, J.H.: Gödel’s ontological proof. In On Being and Saying. Essays for Richard Cartwright, pp. 241–261, MIT Press (1987)
Sobel, J.H.: Logic and Theism: Arguments for and Against Beliefs in God. Cambridge University Press, Cambridge (2004)
Sutcliffe, G.: The TPTP problem library and associated infrastructure. J. Autom. Reasoning 43(4), 337–362 (2009)
Sutcliffe, G., Benzmüller, C.: Automated reasoning in higher-order logic using the TPTP THF infrastructure. J. Formalized Reasoning 3(1), 1–27 (2010)
Tanaka, K.: Three schools of paraconsistency. The Australas. J. Logic 1, 28–42 (2003)
Wenzel, M.: Hoare logic in isabelle. http://isabelle.in.tum.de/dist/library/HOL/HOL-Isar_Examples/Hoare.html
Acknowledgments
We would like to thank João Marcos for consistently useful discussions about discussive logics and paraconsistency. Various persons have contributed or positively influenced this line of research in the past, including, Larry Paulson, Chad Brown, Geoff Sutcliffe, and Jasmin Blanchette.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Benzmüller, C., Woltzenlogel Paleo, B. (2015). Higher-Order Modal Logics: Automation and Applications. In: Faber, W., Paschke, A. (eds) Reasoning Web. Web Logic Rules. Reasoning Web 2015. Lecture Notes in Computer Science(), vol 9203. Springer, Cham. https://doi.org/10.1007/978-3-319-21768-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-21768-0_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-21767-3
Online ISBN: 978-3-319-21768-0
eBook Packages: Computer ScienceComputer Science (R0)


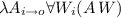 and are represented as in
and are represented as in