Skip to main content
Springer Nature Link
Log in

Asynchronous Dynamics of Boolean Automata Double-Cycles

  • Conference paper
  • First Online:
Unconventional Computation and Natural Computation (UCNC 2015)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 9252))

Abstract

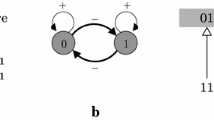
Because interaction networks occupy more and more space in our current life (social networks) and in our understanding of living systems(biological regulation networks), it seems necessary to develop the knowledge regarding them. By using Boolean automata networks as models of interaction networks, we present new results about the influence of cycles on their dynamics. Cycles in the architecture of boolean networks are known to be the primary engine of dynamical complexity. As a first particular case, we focus on cycle intersections and provide a characterisation of the dynamics of asynchronous Boolean automata networks composed of two cycles that intersect at one automaton. To do so, we introduce an efficient formalism inspired by algorithms to define long sequences of updates, which allows a more efficient description of their dynamics.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Demongeot, J., Noual, M., Sené, S.: Combinatorics of Boolean automata circuits dynamics. Discrete Appl. Math. 160, 398–415 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  2. Didier, G., Remy, É.: Relations between gene regulatory networks and cell dynamics in Boolean models. Discrete Appl. Math. 160, 2147–2157 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  3. Fatès, N., Regnault, D., Schabanel, N., Thierry, É.: Asynchronous behavior of double-quiescent elementary cellular automata. In: Correa, J.R., Hevia, A., Kiwi, M. (eds.) LATIN 2006. LNCS, vol. 3887, pp. 455–466. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  4. Goles, E., Martínez, S.: Neural and Automata Networks: Dynamical Behaviour and Applications. Kluwer Academic Publishers, Norwell (1990)

    Book  MATH  Google Scholar 

  5. Ising, E.: Beitrag zur theorie des ferromagnetismus. Z. für Phys. 31, 253–258 (1925)

    Article  Google Scholar 

  6. Jacob, F., Monod, J.: Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 3, 318–356 (1961)

    Article  Google Scholar 

  7. Jacob, F., Perrin, D., Sanchez, C., Monod, J.: L’opéron: groupe de gènes à expression coordonnée par un opérateur. C. R. Hebdomadaires Acad. Sci. 250, 1727–1729 (1960)

    Google Scholar 

  8. Kauffman, S.A.: Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22, 437–467 (1969)

    Article  MathSciNet  Google Scholar 

  9. Kauffman, S.A.: Gene regulation networks: A theory for their global structures and behaviors. In: Moscana, A., Monroy, A. (eds.) Current Topics in Development Biology, vol. 6, pp. 145–181. Elsevier, New York (1971)

    Google Scholar 

  10. McCulloch, W.S., Pitts, W.H.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115–133 (1943)

    Article  MathSciNet  MATH  Google Scholar 

  11. Melliti, T., Noual, M., Regnault, D., Sené, S., Sobieraj, J.: Full characterization of attractors for two intersected asynchronous Boolean automata cycles. Technical report Université d’Évry - Val d’Essonne (2013). arXiv:1310.5747

  12. Melliti, T., Regnault, D., Richard, A., Sené, S.: On the convergence of Boolean automata networks without negative cycles. In: Kari, J., Kutrib, M., Malcher, A. (eds.) AUTOMATA 2013. LNCS, vol. 8155, pp. 124–138. Springer, Heidelberg (2013)

    Chapter  Google Scholar 

  13. Noual, M.: Dynamics of circuits and intersecting circuits. In: Dediu, A.-H., Martín-Vide, C. (eds.) LATA 2012. LNCS, vol. 7183, pp. 433–444. Springer, Heidelberg (2012)

    Chapter  Google Scholar 

  14. Noual, M.: Updating automata networks. Ph.D. thesis, École normale supérieure de Lyon (2012)

    Google Scholar 

  15. Noual, M., Regnault, D., Sené, S.: About non-monotony in Boolean automata networks. Theoret. Comput. Sci. 504, 12–25 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  16. Remy, É., Ruet, P., Thieffry, D.: Graphic requirement for multistability and attractive cycles in a Boolean dynamical framework. Adv. Appl. Math. 41, 335–350 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Richard, A.: Negative circuits and sustained oscillations in asynchronous automata networks. Adv. Appl. Math. 44, 378–392 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Richard, A., Comet, J.P.: Necessary conditions for multistationarity in discrete dynamical systems. Discrete Appl. Math. 155, 2403–2413 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  19. Robert, F.: Discrete Iterations: A Metric Study. Springer, Heidelberg (1986)

    Book  MATH  Google Scholar 

  20. Schelling, T.C.: Dynamic models of segregation. J. Math. Sociol. 1, 143–186 (1971)

    Article  Google Scholar 

  21. Thomas, R.: Boolean formalization of genetic control circuits. J. Theor. Biol. 42, 563–585 (1973)

    Article  Google Scholar 

  22. Thomas, R.: On the relation between the logical structure of systems and their ability to generate multiple steady states or sustained oscillations. In: Dora, J.D., Demongeot, J., Lacolle, B. (eds.) Numerical Methods in the Study of Critical Phenomena. Springer Series in Synergetics, vol. 9, pp. 180–193. Springer, Heidelberg (1981)

    Chapter  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. IBISC, EA4526, Université d’Évry Val-d’Essonne, 91037, Évry, France

    Tarek Melliti, Damien Regnault & Jérémy Sobieraj

  2. Aix-Marseille Université, CNRS, LIF UMR 7279, 13288, Marseille, France

    Mathilde Noual & Sylvain Sené

  3. IXXI, Institut Rhône-alpin des systèmes complexes, 69007, Lyon, France

    Sylvain Sené

Authors
  1. Tarek Melliti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mathilde Noual
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Damien Regnault
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sylvain Sené
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jérémy Sobieraj
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tarek Melliti .

Editor information

Editors and Affiliations

  1. University of Auckland, Auckland, New Zealand

    Cristian S. Calude

  2. University of Auckland, Auckland, New Zealand

    Michael J. Dinneen

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer International Publishing Switzerland

About this paper

Cite this paper

Melliti, T., Noual, M., Regnault, D., Sené, S., Sobieraj, J. (2015). Asynchronous Dynamics of Boolean Automata Double-Cycles. In: Calude, C., Dinneen, M. (eds) Unconventional Computation and Natural Computation. UCNC 2015. Lecture Notes in Computer Science(), vol 9252. Springer, Cham. https://doi.org/10.1007/978-3-319-21819-9_19

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-21819-9_19

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-21818-2

  • Online ISBN: 978-3-319-21819-9

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics