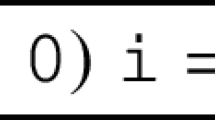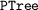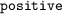Abstract
The problem of computing dominators in a control flow graph is central to numerous modern compiler optimizations. Many efficient algorithms have been proposed in the literature, but mechanizing the correctness of the most sophisticated algorithms is still considered as too hard problems, and to this date, verified compilers use less optimized implementations. In contrast, production compilers, like GCC or LLVM, implement the classic, efficient Lengauer-Tarjan algorithm [12], to compute dominator trees. And subsequent optimization phases can then determine whether a CFG node dominates another node in constant time by using their respective depth-first search numbers in the dominator tree. In this work, we aim at integrating such techniques in verified compilers. We present a formally verified validator of untrusted dominator trees, on top of which we implement and prove correct a fast dominance test following these principles. We conduct our formal development in the Coq proof assistant, and integrate it in the middle-end of the CompCertSSA verified compiler. We also provide experimental results showing performance improvement over previous formalizations.
This work was supported by Agence Nationale de la Recherche, grant number ANR-14-CE28-0004 DISCOVER.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Such a property would be required to prove completeness: if a node d dominates a node n then the dominance test on (d, n) should succeed. To our experience in verified compilation, we never make usage of such a completeness property. The property holds, but we do not need to prove it in Coq.
- 2.
Not to be confused with the control flow graph here.
- 3.
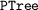
is a dictionary implementation using Patricia trees provided in CompCert. Type \(\mathtt {(Ptree.t~a)}\) denotes an associative, partial map with keys of type \(\mathtt {positive}\) – binary encoding of strictly positive integers – with associated data of type \(\mathtt {a}\). In this paper, types \(\mathtt {node}\) and \(\mathtt {positive}\) are synonyms.
- 4.
We write m!n the lookup of a key

in a map

.
- 5.
Recall that we rely on the standard implementation of positive integers,
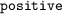
.
- 6.
The impact of building and using the dominance test is currently negligible compared to the whole compilation time, as, currently, certain compiler passes (such as the SSA deconstruction) would need performance improvement.
References
Allen, F.E., Cocke, J.: Graph theoretic constructs for program control flow analysis. Technical report, IBM T.J. Watson Research Center (1972)
Barthe, G., Demange, D., Pichardie, D.: Formal verification of an SSA-based middle-end for CompCert. ACM TOPLAS 36(1), 4:1–4:35 (2014)
Chlipala, A.: A verified compiler for an impure functional language. In: POPL 2010, pp. 93–106. ACM (2010)
Cooper, K.D., Harvey, T.J., Kennedy, K.: A simple, fast dominance algorithm. Technical report, Rice University (2006)
Cytron, R., Ferrante, J., Rosen, B.K., Wegman, M.N., Zadeck, F.K.: Efficiently computing static single assignment form and the control dependence graph. ACM TOPLAS 13(4), 451–490 (1991)
Dargaye, Z., Leroy, X.: Mechanized verification of CPS transformations. In: Dershowitz, N., Voronkov, A. (eds.) LPAR 2007. LNCS (LNAI), vol. 4790, pp. 211–225. Springer, Heidelberg (2007)
Demange, D., Pichardie, D., Stefanesco, L.: Verifying fast and sparse SSA-based optimizations in Coq. In: Franke, B. (ed.) CC 2015. LNCS, vol. 9031, pp. 233–252. Springer, Heidelberg (2015)
Fluet, M., Weeks, S.: Contification using dominators. In: Proceedings of ICFP 2001, pp. 2–13. ACM (2001)
Georgiadis, L., Laura, L., Parotsidis, N., Tarjan, R.E.: Dominator certification and independent spanning trees: an experimental study. In: Demetrescu, C., Marchetti-Spaccamela, A., Bonifaci, V. (eds.) SEA 2013. LNCS, vol. 7933, pp. 284–295. Springer, Heidelberg (2013)
Georgiadis, L., Tarjan, R.E., Werneck, R.F.: Finding dominators in practice. J. Graph Algorithms Appl. 10(1), 69–94 (2006)
Georgiadis, L., Tarjan, R.E.: Dominator tree verification and vertex-disjoint paths. In: Proceedings of SODA 2005, pp. 433–442. ACM (2005)
Lengauer, T., Tarjan, R.E.: A fast algorithm for finding dominators in a flowgraph. ACM TOPLAS 1(1), 121–141 (1979)
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7), 107–115 (2009)
Leroy, X.: A formally verified compiler back-end. JAR 43(4), 363–446 (2009)
Okasaki, C., Gill, A.: Fast mergeable integer maps. In: Workshop on ML, pp. 77–86 (1998)
Parotsidis, N., Georgiadis, L.: Dominators in directed graphs: a survey of recent results, applications, and open problems. In: 2nd International Symposium on Computing in Informatics and Mathematics (ISCIM 2013), vol. 1, pp. 15–20. Epoka University (2013)
Rivest, R.L., Cormen, T.H., Leiserson, C.E., Stein, C.: Introduction to Algorithms, 3rd edn. MIT Press, Cambridge (2009)
Zhao, J., Nagarakatte, S., Martin, M., Zdancewic, S.: Formal verification of SSA-based optimizations for LLVM. In: PLDI 2013, pp. 175–186. ACM (2013)
Zhao, J., Zdancewic, S.: Mechanized verification of computing dominators for formalizing compilers. In: Hawblitzel, C., Miller, D. (eds.) CPP 2012. LNCS, vol. 7679, pp. 27–42. Springer, Heidelberg (2012)
Zhao, J., Zdancewic, S., Nagarakatte, S., Martin, M.: Formalizing the LLVM intermediate representation for verified program transformation. In: POPL 2012, pp. 427–440. ACM (2012)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Blazy, S., Demange, D., Pichardie, D. (2015). Validating Dominator Trees for a Fast, Verified Dominance Test. In: Urban, C., Zhang, X. (eds) Interactive Theorem Proving. ITP 2015. Lecture Notes in Computer Science(), vol 9236. Springer, Cham. https://doi.org/10.1007/978-3-319-22102-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-22102-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22101-4
Online ISBN: 978-3-319-22102-1
eBook Packages: Computer ScienceComputer Science (R0)