Skip to main content
Springer Nature Link
Log in

Exhaustive Vacation Queue with Dependent Arrival and Service Processes

  • Conference paper
Queueing Theory and Network Applications (QTNA 2015)

Part of the book series: Advances in Intelligent Systems and Computing ((AISC,volume 383))

Included in the following conference series:

  • 1455 Accesses

Abstract

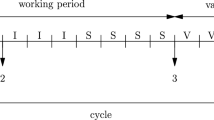
This paper presents a more general class of MAP/MAP/1 exhaustive vacation queue, in which the Markov modulated arrival and service processes are dependent. This model class requires the evaluation of the busy period of quasi birth death process with arbitrary initial level, which is a new analysis element.

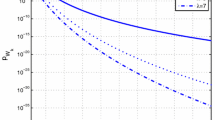
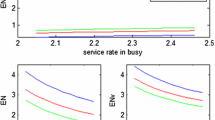
The model is analyzed by applying matrix analytic methods for the underlying quasi birth death process. The main result of the paper is the probability-generating function of the number of jobs in the system. Finally, a numerical example provides an insight into the behavior of the model.

The authors thank the support of the OTKA K101150 project.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Alfa, A.S.: A discrete MAP/PH/1 queue with vacations and exhaustive time-limited service. Oper. Res. Lett. 18, 31–40 (1995)

    Article  MathSciNet  Google Scholar 

  2. Alfa, A.S.: Discrete time analysis of MAP/PH/1 vacation queue with gated time-limited service. Queueing Systems 29(1), 35–54 (1998)

    Article  MathSciNet  Google Scholar 

  3. Goswami, C., Selvaraju, N.: The discrete-time MAP/PH/1 queue with multiple working vacations. Applied Mathematical Modelling 34, 931–946 (2010)

    Article  MathSciNet  Google Scholar 

  4. Chang, S., Takine, T.: Factorization and stochastic decomposition properties in bulk queues with generalized vacations. Queueing Systems 50(2–3), 165–183 (2005)

    Article  MathSciNet  Google Scholar 

  5. Ke, J.C., Wu, C.H., Zhang, Z.G.: Recent developments in vacation queueing models: a short survey. International Journal of Operations Research 7(4), 3–8 (2010)

    Google Scholar 

  6. Latouche, G., Ramaswami, V.: Introduction to matrix analytic methods in stochastic modeling, vol. 5. SIAM (1999)

    Google Scholar 

  7. Neuts, M.F.: A versatile markovian point process. Journal of Applied Probability, 764–779 (1979)

    Article  MathSciNet  Google Scholar 

  8. Saffer, Z., Telek, M.: Analysis of BMAP/G/1 vacation model of non-M/G/1-type. In: Thomas, N., Juiz, C. (eds.) EPEW 2008. LNCS, vol. 5261, pp. 212–226. Springer, Heidelberg (2008)

    Chapter  Google Scholar 

  9. Saffer, Z., Telek, M.: Closed form results for BMAP/G/1 vacation model with binomial type disciplines. Publ. Math. Debrecen 76(3), 359–378 (2010)

    MathSciNet  MATH  Google Scholar 

  10. Tian, N., Zhang, Z.G.: Vacation queueing models: theory and applications, vol. 93. Springer Science & Business Media (2006)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Budapest University of Technology and Economics, Budapest, Hungary

    Gábor Horváth, Zsolt Saffer & Miklós Telek

  2. MTA-BME Information Systems Research Group, Budapest, Hungary

    Gábor Horváth & Miklós Telek

Authors
  1. Gábor Horváth
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zsolt Saffer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Miklós Telek
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gábor Horváth .

Editor information

Editors and Affiliations

  1. Department of Networked Systems and Services, Budapest University of Technology and Economics, Budapest, Hungary

    Tien van Do

  2. Department of Systems Science, Kyoto University Graduate School of Informatics, Kyoto, Japan

    Yutaka Takahashi

  3. Faculty of Science and Engineering, Department of Information Science and Systems Engineering, Konan University, Kobe, Japan

    Wuyi Yue

  4. Faculty of Information Technology, VNU University of Engineering and Technology, Hanoi, Vietnam

    Viet-Ha Nguyen

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer International Publishing Switzerland

About this paper

Cite this paper

Horváth, G., Saffer, Z., Telek, M. (2016). Exhaustive Vacation Queue with Dependent Arrival and Service Processes. In: van Do, T., Takahashi, Y., Yue, W., Nguyen, VH. (eds) Queueing Theory and Network Applications. QTNA 2015. Advances in Intelligent Systems and Computing, vol 383. Springer, Cham. https://doi.org/10.1007/978-3-319-22267-7_2

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-22267-7_2

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-22266-0

  • Online ISBN: 978-3-319-22267-7

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics