Skip to main content
Springer Nature Link
Log in

Computing Topology Preservation of RBF Transformations for Landmark-Based Image Registration

  • Conference paper
  • First Online:
Curves and Surfaces (Curves and Surfaces 2014)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 9213))

Included in the following conference series:

  • 1125 Accesses

Abstract

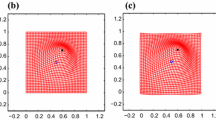
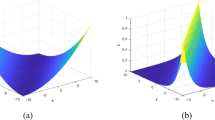
In image registration, a proper transformation should be topology preserving. Especially for landmark-based image registration, if the displacement of one landmark is larger enough than those of neighbourhood landmarks, topology violation will be occurred. This paper aims to analyse the topology preservation of some Radial Basis Functions (RBFs) which are used to model deformations in image registration. Matérn functions are quite common in the statistic literature (see, e.g. [9, 13]). In this paper, we use them to solve the landmark-based image registration problem. We present the topology preservation properties of RBFs in one landmark and four landmarks model respectively. Numerical results of three kinds of Matérn transformations are compared with results of Gaussian, Wendland’s, and Wu’s functions.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Allasia, G., Cavoretto, R., De Rossi, A.: Local interpolation schemes for landmark-based image registration: a comparison. Math. Comput. Simul. 106, 1–25 (2014)

    Article  Google Scholar 

  2. Arad, N., Dyn, N., Reisfeld, D., Yeshurun, Y.: Warping by radial basis functions: application to facial expressions. CVGIP Graph. Models Image Process. 56, 161–172 (1994)

    Article  Google Scholar 

  3. Cavoretto, R., De Rossi, A.: Landmark-based image registration using Gneiting’s compactly supported functions. In: Simos, T.E., et al. (eds.) Proceedings of the ICNAAM 2012, AIP Conference Proceedings, vol. 1479, Melville, New York, pp. 1335–1338 (2012)

    Google Scholar 

  4. Cavoretto, R., De Rossi, A.: Analysis of compactly supported transformations for landmark-based image registration. Appl. Math. Inf. Sci. 7, 2113–2121 (2013)

    Article  MathSciNet  Google Scholar 

  5. De Rossi, A.: Medical image registration using compactly supported functions. Commun. Appl. Ind. Math. 4, 1–12 (2013)

    Google Scholar 

  6. Fasshauer, G.E.: Meshfree Approximation Methods with MATLAB. World Scientific Publishers Co., Inc., River Edge (2007)

    Book  MATH  Google Scholar 

  7. Fornefett, M., Rohr, K., Stiehl, H.: Radial basis functions with compact support for elastic registration of medical images. Image Vis. Comput. 19, 87–96 (2001)

    Article  Google Scholar 

  8. Gneiting, T., Kleiber, W., Schlather, M.: Matérn cross-covariance functions for multivariate random fields. J. Amer. Statist. Assoc. 105, 1167–1177 (2010)

    Article  MathSciNet  Google Scholar 

  9. Matérn, B.: Spatial Variation. Lecture Notes in Statistics, vol. 36. Springer, New York (1986)

    Google Scholar 

  10. Modersitzki, J.: FAIR: Flexible Algorithms for Image Registration, vol. 6. SIAM, Philadelphia (2009)

    Book  Google Scholar 

  11. Rohr, K.: Landmark-Based Image Analysis, Using Geometric and Intensity Models. Kluwer Academic Publishers, Norwell (2001)

    Book  Google Scholar 

  12. Scherzer, O.: Mathematical Models for Registration and Applications to Medical Imaging. Springer, Heidelberg (2006)

    Book  MATH  Google Scholar 

  13. Stein, M.L.: Interpolation of Spatial Data: Some Theory for Kriging. Springer, New York (1999)

    Book  MATH  Google Scholar 

  14. Wendland, H.: Scattered Data Approximation, vol. 17. Cambridge Univsity Press, Cambridge (2005)

    MATH  Google Scholar 

  15. Wu, Z.: Compactly supported positive definite radial functions. Adv. Comput. Math 4, 283–292 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  16. Yang, X., Xue, Z., Lia, X., Xiong, D.: Topology preservation evaluation of compact-support radial basis functions for image registration. Pattern Recogn. Lett. 32, 1162–1177 (2011)

    Article  Google Scholar 

  17. Zitová, B., Flusser, J.: Image registration methods: a survey. Image Vis. Comput. 21, 977–1000 (2003)

    Article  Google Scholar 

Download references

Acknowledgments

The work of the first author is partially supported by the University of Torino via grant “Approssimazione di dati sparsi e sue applicazioni”. The second author acknowledges financial support from the GNCS–INdAM. The authors also sincerely thank the anonymous referee for helping to significantly improve this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics “G. Peano”, University of Torino, Via Carlo Alberto 10, 10123, Torino, Italy

    Roberto Cavoretto, Alessandra De Rossi & Hanli Qiao

  2. Innsbruck Medical University, Anichstrasse 35, 6020, Innsbruck, Austria

    Bernhard Quatember & Wolfgang Recheis

  3. University of Applied Science, J. Gutenberg Straße 3, 2700, Wiener Neustadt, Austria

    Martin Mayr

Authors
  1. Roberto Cavoretto
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alessandra De Rossi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hanli Qiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Bernhard Quatember
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wolfgang Recheis
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Martin Mayr
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alessandra De Rossi .

Editor information

Editors and Affiliations

  1. INRIA, Sophia Antipolis, Sophia Antipolis, France

    Jean-Daniel Boissonnat

  2. École Normale Supérieure, Paris, France

    Albert Cohen

  3. Arts Et Metiers ParisTech Lab de Sciences de l'Information, Paris, France

    Olivier Gibaru

  4. INSA de Rouen, LMI, Saint-Étienne-du-Rouvray, France

    Christian Gout

  5. Department of Mathematics, University of Oslo, Oslo, Norway

    Tom Lyche

  6. Université Joseph Fourier, Grenoble, France

    Marie-Laurence Mazure

  7. Department of Mathematics, Vanderbilt University, Nashville, Tennessee, USA

    Larry L. Schumaker

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer International Publishing Switzerland

About this paper

Cite this paper

Cavoretto, R., De Rossi, A., Qiao, H., Quatember, B., Recheis, W., Mayr, M. (2015). Computing Topology Preservation of RBF Transformations for Landmark-Based Image Registration. In: Boissonnat, JD., et al. Curves and Surfaces. Curves and Surfaces 2014. Lecture Notes in Computer Science(), vol 9213. Springer, Cham. https://doi.org/10.1007/978-3-319-22804-4_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-22804-4_8

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-22803-7

  • Online ISBN: 978-3-319-22804-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics