Abstract
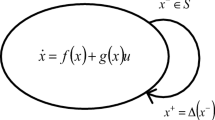
The improvement of stability for dynamic biped walking is motivated by the potential use of humanoid robot in complex environment. This paper focuses on the effect of ground compliance on the periodic stability of dynamic walking. Firstly, the compliant ground is equivalent to a spring-damper system, and the coupling dynamics model of robot-ground system is modelled as a rigid planar kinematic chains in contact with a stiffness-damping system. Based on it, two differential equations are obtained to describe the dynamic walking process in one cycle which is separated into a swing phase followed by an impact phase. Subsequently, a stable gait is planned under rigid assumption and transplanted to the walking under compliant ground condition. The effect of ground compliance on the gait during the swing phases is analyzed under 15 kinds of ground conditions, respectively and effect on it during impact phase is analyzed under 12 kinds of ground conditions. Finally, the periodic stability under the effect of ground compliance is analyzed with 6 kinds of ground conditions, and the effect of ground compliance on the periodic stability of dynamic walking is concluded.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
McGeer, T.: Passive dynamic walking. The International Journal of Robotics Research 9(2), 62–82 (1990)
Griffin, B., Grizzle, J.: Walking gait optimization for accommodation of unknown terrain height variations. In: American Control Conference (2015) (Submitted on 25 September 2014)
Dai, H. Tedrake, R.: Optimizing robust limit cycles for legged locomotion on unknown terrain. In: CDC, pp. 1207–1213 (2012)
Byl, K., Tedrake, R.: Metastable walking machines. International Journal of Robotics Research 28(8), 1040–1064 (2008)
Zhao, H., Powell, M.J., Ames, A.D.: Human-inspired motion primitives and transitions for bipedal robotic locomotion in diverse terrain. Optimal Control Applications and Methods 35(6), 730–755 (2014)
Ames, A.D., Cousineau, E.A., Powell, M.J.: Dynamically stable bipedal robotic walking with NAO via human-inspired hybrid zero dynamics. In: Proceedings of the 15th ACM International Conference on Hybrid Systems: Computation and Control, pp. 135–144 (2012)
Spong, M.W., Bullo, F.: Controlled symmetries and passive walking. IEEE Transactions on Automatic Control 50(7), 1025–1031 (2005)
Hu, Y., Yan, G., Lin, Z.: Stable walking for a compass-like biped robot in complex environments. In: American Control Conference (ACC), pp. 6048–6053 (2010)
Hurmuzlu, Y., Marghitu, D.B.: Rigid body collisions of planar kinematic chains with multiple contact points. The international journal of robotics research 13(1), 82–92 (1994)
Bicchi, A., Kumar, V.: Robotic grasping and contact: A review. In: ICRA, pp. 348–353 (2000)
Lens, T., Radkhah, K., von Stryk, O.: Simulation of dynamics and realistic contact forces for manipulators and legged robots with high joint elasticity. In: IEEE International Conference on Advanced Robotics (ICAR), pp. 34–41 (2011)
Stronge, W.J., James, R., Ravani, B.: Oblique impact with friction and tangential compliance. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 359(1789), 2447–2465 (2001)
Stronge, W.J.: Rigid body collisions with friction. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences 431(1881), 169–181 (1990)
Marhefka, D.W., Orin, D.E.: Simulation of contact using a nonlinear damping model. In: Proceedings of IEEE International Conference on Robotics and Automation, 1996, vol. 2, pp. 1662–1668 (1996)
Chevallereau, C., Grizzle, J.W., Shih, C.L.: Asymptotically stable walking of a five-link underactuated 3-D bipedal robot. IEEE Transactions on Robotics 25(1), 37–50 (2009)
Grizzle, J.W., Abba, G., Plestan, F.: Asymptotically stable walking for biped robots: Analysis via systems with impulse effects. IEEE Transactions on Automatic Control 46(1), 51–64 (2001)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Wang, Y., Ding, J., Xiao, X. (2015). Periodic Stability for 2-D Biped Dynamic Walking on Compliant Ground. In: Liu, H., Kubota, N., Zhu, X., Dillmann, R., Zhou, D. (eds) Intelligent Robotics and Applications. ICIRA 2015. Lecture Notes in Computer Science(), vol 9245. Springer, Cham. https://doi.org/10.1007/978-3-319-22876-1_32
Download citation
DOI: https://doi.org/10.1007/978-3-319-22876-1_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22875-4
Online ISBN: 978-3-319-22876-1
eBook Packages: Computer ScienceComputer Science (R0)