Abstract
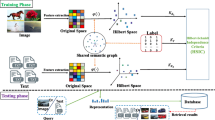
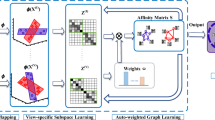
Many real-world datasets are represented by multiple features or modalities which often provide compatible and complementary information to each other. In order to obtain a good data representation that synthesizes multiple features, researchers have proposed different multi-view subspace learning algorithms. Although label information has been exploited for guiding multi-view subspace learning, previous approaches either fail to directly capture the semantic relations between labeled items or unrealistically make Gaussian assumption about data distribution. In this paper, we propose a new multi-view nonnegative subspace learning algorithm called Multi-view Semantic Learning (MvSL). MvSL tries to capture the semantic structure of multi-view data by a novel graph embedding framework. The key idea is to let neighboring intra-class items be near each other while keep nearest inter-class items away from each other in the learned common subspace across multiple views. This nonparametric scheme can better model non-Gaussian data. To assess nearest neighbors in the multi-view context, we develop a multiple kernel learning method for obtaining an optimal kernel combination from multiple features. In addition, we encourage each latent dimension to be associated with a subset of views via sparseness constraints. In this way, MvSL is able to capture flexible conceptual patterns hidden in multi-view features. Experiments on two real-world datasets demonstrate the effectiveness of the proposed algorithm.
Chapter PDF
Similar content being viewed by others
Keywords
References
Amini, M., Usunier, N., Goutte, C.: Learning from multiple partially observed views-an application to multilingual text categorization. In: Advances in Neural Information Processing Systems, pp. 28–36 (2009)
Cai, D., He, X., Han, J., Huang, T.S.: Graph regularized nonnegative matrix factorization for data representation. IEEE Transactions on Pattern Analysis and Machine Intelligence 33(8), 1548–1560 (2011)
Chen, N., Zhu, J., Xing, E.P.: Predictive subspace learning for multi-view data: a large margin approach. In: Advances in Neural Information Processing Systems, pp. 361–369 (2010)
Han, Y., Wu, F., Tao, D., Shao, J., Zhuang, Y., Jiang, J.: Sparse unsupervised dimensionality reduction for multiple view data. IEEE Transactions on Circuits and Systems for Video Technology 22(10), 1485–1496 (2012)
He, J., Chang, S.-F., Xie, L.: Fast kernel learning for spatial pyramid matching. In: IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2008, pp. 1–7. IEEE (2008)
Hidru, D., Goldenberg, A.: Equinmf: Graph regularized multiview nonnegative matrix factorization (2014). arXiv preprint arXiv:1409.4018
Hotelling, H.: Relations between two sets of variates. Biometrika 321–377 (1936)
Hoyer, P.O.: Non-negative sparse coding. In: Proceedings of the 2002 12th IEEE Workshop on Neural Networks for Signal Processing, pp. 557–565 (2002)
Jia, Y., Salzmann, M., Darrell, T.: Factorized latent spaces with structured sparsity. In: Advances in Neural Information Processing Systems, pp. 982–990 (2010)
Jiang, Y., Liu, J., Li, Z., Lu, H.: Semi-supervised unified latent factor learning with multi-view data. Machine Vision and Applications 25(7), 1635–1645 (2014)
Kalayeh, M., Idrees, H., Shah, M.: NMF-KNN: Image annotation using weighted multi-view non-negative matrix factorization. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 184–191 (2014)
Kim, J., Monteiro, R., Park, H.: Group sparsity in nonnegative matrix factorization. In: SDM, pp. 851–862. SIAM (2012)
Lee, D.D., Seung, H.S.: Learning the parts of objects by non-negative matrix factorization. Nature 401(6755), 788–791 (1999)
Li, H., Wang, M., Hua, X.-S.: Msra-mm 2.0: A large-scale web multimedia dataset. In: IEEE International Conference on Data Mining Workshops, pp. 164–169. IEEE (2009)
Lin, C.-J.: Projected gradient methods for nonnegative matrix factorization. Neural computation 19(10), 2756–2779 (2007)
Liu, H., Wu, Z., Li, X., Cai, D., Huang, T.S.: Constrained nonnegative matrix factorization for image representation. IEEE Transactions on Pattern Analysis and Machine Intelligence 34(7), 1299–1311 (2012)
Liu, J., Jiang, Y., Li, Z., Zhou, Z.-H., Lu, H.: Partially shared latent factor learning with multiview data (2014)
Liu, J., Wang, C., Gao, J., Han, J.: Multi-view clustering via joint nonnegative matrix factorization. In: Proc. of SDM, vol. 13, pp. 252–260 (2013)
Sha, F., Lin, Y., Saul, L.K., Lee, D.D.: Multiplicative updates for nonnegative quadratic programming. Neural Computation 19(8), 2004–2031 (2007)
Shawe-Taylor, N., Kandola, A.: On kernel target alignment. Advances in neural information processing systems 14, 367 (2002)
Wang, Y., Jia, Y.: Fisher non-negative matrix factorization for learning local features. In: Proc. Asian Conf. on Comp. Vision. Citeseer (2004)
Xia, T., Tao, D., Mei, T., Zhang, Y.: Multiview spectral embedding. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics 40(6), 1438–1446 (2010)
Xu, C., Tao, D., Xu, C.: A survey on multi-view learning. arXiv preprint arXiv:1304.5634 (2013)
Yan, S., Xu, D., Zhang, B., Zhang, H.-J., Yang, Q., Lin, S.: Graph embedding and extensions: a general framework for dimensionality reduction. IEEE Transactions on Pattern Analysis and Machine Intelligence 29(1), 40–51 (2007)
Zafeiriou, S., Tefas, A., Buciu, I., Pitas, I.: Exploiting discriminant information in nonnegative matrix factorization with application to frontal face verification. IEEE Transactions on Neural Networks 17(3), 683–695 (2006)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Luo, P., Peng, J., Guan, Z., Fan, J. (2015). Multi-view Semantic Learning for Data Representation. In: Appice, A., Rodrigues, P., Santos Costa, V., Soares, C., Gama, J., Jorge, A. (eds) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2015. Lecture Notes in Computer Science(), vol 9284. Springer, Cham. https://doi.org/10.1007/978-3-319-23528-8_23
Download citation
DOI: https://doi.org/10.1007/978-3-319-23528-8_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-23527-1
Online ISBN: 978-3-319-23528-8
eBook Packages: Computer ScienceComputer Science (R0)