Abstract
Attribute-based encryption has the potential to be deployed in a cloud computing environment to provide scalable and fine-grained data sharing. However, user revocation within ABE deployment remains a challenging issue to overcome, particularly when there is a large number of users. In this work, we introduce an extended proxy-assisted approach, which weakens the trust required of the cloud server. Based on an all-or-nothing principle, our approach is designed to discourage a cloud server from colluding with a third party to hinder the user revocation functionality. We demonstrate the utility of our approach by presenting a construction of the proposed approach, designed to provide efficient cloud data sharing and user revocation. A prototype was then implemented to demonstrate the practicality of our proposed construction.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Cloud storage services (e.g. Dropbox, Microsoft’s Azure storage, and Amazon’s S3) enable users to upload and store their data remotely in the cloud environment as well as accessing and downloading the remotely stored data in real-time using a web browser or a mobile application [24]. To ensure the security and privacy of user data [9], particularly against an untrusted cloud service provider, one could encrypt the data prior to uploading and storing the data in the cloud [8, 10, 11, 15, 16, 18, 35]. In practice, data encryption often serves as an access control mechanism in cloud data sharing, where end users’ decryption capabilities are defined based on a specified access control policy. For instance, a scientific research team may choose to share their research data and findings (that are stored in a cloud server) in real-time with their team workers [19], based on some pre-determined attributes or roles. To provide the scalability and flexibility of real-time data sharing, a fine-grained access control is required. Attribute-based encryption (ABE) [4, 13, 14, 20, 28] has been identified as a suitable solution to enforce fine-grained decryption rights.
ABE can be broadly categorized into key policy ABE (KP-ABE) and ciphertext policy ABE (CP-ABE). KP-ABE allows data to be encrypted with a set of attributes, and each decryption key is associated with an access policy (defined in terms of attributes); while CP-ABE is complementary – data are encrypted and tagged with the pre-determined access policy, and a decryption key is associated with the set of attributes. In either type, a ciphertext can be decrypted using the corresponding decryption key only if the attributes satisfy the access policy. ABE has been shown to be an effective and scalable access control mechanism for encrypted data, but one key limiting factor is user revocation in an environment where there are many users (e.g. in a cloud storage environment).
There are several possible approaches to address this challenge. For example, one could implement an authentication based revocation mechanism in a conventional access control system. However, such an approach requires the cloud server to be fully trusted. This approach also imposes additional computational requirements on both the users and the cloud server – the users are required to possess another authentication secret and the cloud server needs to deal with the additional authentication. Another potential approach is the key-update based revocation, such as those proposed in [17, 29, 34], where key materials will be updated to exclude a revoked user. This approach, however, suffers from limited scalability as all data must be re-encrypted, and all non-revoked legitimate user keys need to be either updated or re-distributed. This is prohibitive in a data-intensive and high user volume environment, such as cloud storage. Although in [17, 29, 34] the majority of data re-encryption workload is often performed by the cloud server, it remains an attractive option to reduce the computational requirements in a real-world implementation.
Several researchers have introduced an alternative approach for user revocation by introducing an “expiry time” attribute such that a decryption key is effective only for a period of time [4, 13]. The shortcoming of this method is that it is not possible to do real-time user revocation. Ostrovsky et al. [23] employ negative constrains in access policy, such that a revocation of certain attributes amounts to negating the attributes. The system does not scale well in the revoking of individual users, because each encryption requires the information of all revoked users and each of which is treated as a distinctive attribute. Attrapadung et al. [1] aim to solve the revocation problem by incorporating the broadcast encryption revocation mechanism [22] into ABE. The resulting scheme, however, generates the public system key in size proportional to the total number of users. Consequently, such a scheme has limited scalability. The scheme introduced in [21] attempts to leverage revocation and traceability to ABE in real-world applications, such as Pay-TV, where a decryption key is contained in a black-box. The scheme is, unfortunately, not practical as the size of each of public key, private key and ciphertext is O(n), where n is the total number of users.
More recently, proxy-assisted user revocation was introduced in [32, 33, 35] as a potential solution. In this approach, a cloud server acts as a proxy, and each user’s decryption capability is split and represented by two parts, namely: the first part is held by the cloud server (i.e. cloud-side key), and the other is held by the user (i.e. user-side key). A decryption requires a partial decryption using the cloud-side key by the cloud server, and a final/full decryption using the user-side key by the user. In user revocation, the cloud server will erase the key associated with the user to be revoked. This method is particularly promising, as it supports immediate revocation, without compromising efficiency as it does not require data re-encryption or key update. The idea of recurring to a third party for immediate user revocation could be traced back to mediated cryptography, where a mediator is introduced for the purpose of user revocation (e.g. [3]). The difference between proxy-assisted user revocation (e.g. [32, 33, 35]) and mediated cryptography will be clarified in Sect. 2.
However, we observe that both proxy-assisted and mediated cryptography approaches require the cloud server to be trusted, which as pointed out in [5] that ‘there are legitimate concerns about cloud service providers being compelled to hand over user data that reside in the cloud to government agencies without the user’s knowledge or consent due to territorial jurisdiction by a foreign government’. In the aftermath of the revelations by Edward Snowden that the National Security Agency has been conducting wide-scale government surveillance, including those targeting cloud users - see http://masssurveillance.info/, the requirement of a honest cloud server (in this context, the cloud server is assumed not to disclose users’ cloud-side keys) may limit the adoption of the proxy-assisted approach or the mediated cryptography approach. Key disclosure could also be due to unscrupulous employees of the cloud service provider or an attacker who has successfully compromised the cloud system.
Our Contributions. We are, thus, motivated to address this problem; extending the proxy/mediator assisted user revocation approach (based on an ‘all-or-nothing’ principle) to mitigate the risk due to a dishonest cloud server. More specifically, the private key of the cloud server is also required for the cloud-side partial decryption. Consequently, in order for the cloud server to collude with another user to disclose a user’s cloud-side key, the cloud server would also have to reveal its private key in order to perform a partial decryption. We coin this approach as an extended proxy-assisted user revocation. We regard the contributions of this work to be three-fold: (1) We formulate the definition and threat model for cloud data encryption using the extended proxy-assisted user revocation; (2) We propose a concrete construction instantiating our extended proxy-assisted approach, which demonstrates the utility of this approach; and (3) We implement a prototype of our construction, which demonstrates the practicality of our proposed construction.
2 Related Work
Cloud Data Encryption with ABE. Over the last decade, a large number of cloud data encryption schemes have been proposed in the literature. Of particular relevance are those that utilize ABE. As an one-to-many encryption scheme, ABE is required to provide user revocation. However, the various proposed attribute revocation mechanisms for ABE, such as “expiry time” attributes and negative attributes [1, 4, 13, 21, 23], are generally not suitable for cloud data encryption deployment as discussed below and in the preceding section.
Yu et al. [34] suggested adopting KP-ABE to achieve fine-grained data sharing. To support user revocation, they proposed using proxy re-encryption (PRE) [2] in the updating of user’s decryption key. In this approach, the bulk of the computationally expensive operations (e.g. re-generation of encrypted cloud data due to user revocation) are performed by the cloud server. Although a cloud generally has significantly more computational resources, each user’s quota is cost-based. Similar limitation is observed in the scheme proposed by Wang et al. [29]. Sahai et al. [26] proposed an attribute revocable CP-ABE scheme, using ciphertext delegation and the piecewise property of private keys. In particular, the system proceeds in epochs, and in each epoch, the attribute authority generates a set of update keys (as the other piece of each private key) according to the revocation list. All the ciphertexts are then re-encrypted with a new access policy (the principal access policy remains unchanged, but the extra access policy changes in each epoch). A similar attribute revocation method has also been explored in the multi-authority setting [30, 31], where users’ attributes are issued by multiple independent attribute authorities. Similar to other ABE schemes with built-in attribute revocation support (such as expiry time and negative attributes), these schemes face the challenge of transforming attribute revocation into efficient revocation for individual users. In addition, the overheads introduced by these schemes in the re-generation of encrypted data should be addressed. In our extended proxy-assisted approach, however, the overhead imposed upon both the cloud server and users due to user revocation is relatively less.
Mediated Cryptography. Boneh et al. proposed “mediated RSA” to split the private key of RSA into two shares; one share is delegated to an online “mediator” and the other is given to the user [3]. As RSA decryption and signing require the collaboration of both parties, the user’s cryptographic capabilities are immediately revoked if the mediator does not cooperate. Recently, Chen et al. [7] presented a mediated CP-ABE scheme, where the mediator’s key is issued over a set of attributes. The scheme in [12] can also be viewed as mediated ABE, although its purpose is to outsource the costly ABE decryption to the mediator. This does now result in immediate revocation. A common issue associated with existing mediated cryptographic schemes is key escrow. In other words, there is a party responsible for generating the key shares such that the party knows both shares. Similar to our proposed extended proxy-assisted approach, mediated cryptography is intended to provide immediate user revocation (we remark that mediator and proxy are essentially the same concept). However, a key difference between the (extended) proxy-assisted approach and the mediated cryptography is that the former approach does not suffer from the key escrow problem, since the shares are generated by different parties and no single party knows both shares. This is a particularly attractive option in the current privacy conscious landscape.
Unlike other mediated schemes, the mediated certificateless encryption [6] avoids key escrow by employing a combination of identity-based encryption and conventional public key encryption; the private key corresponding to the identity-based encryption held by the mediator is generated by a key generation authority, and the private key of public key encryption can be generated by the user. Unfortunately, such an approach cannot be straightforwardly used in the (extended) proxy-assisted approach by simply replacing identity based encryption with ABE. This is due to the fact that using ABE for data encryption, the encryptor does not have any particular recipients. Both the mediated certificateless encryption (as well as other mediated cryptographic schemes) and the proxy-assisted approach (such as those in [32, 35]) require the mediator/proxy to be honest in maintaining user’s key shares. As mentioned earlier, this may not be a realistic assumption to privacy conscious (or paranoid) users. Our extended proxy-assisted approach exactly is designed to address this issue.
3 Proposed Revocable Cloud Data Encryption Model
3.1 System Overview
A cloud storage system allows an owner to remotely store the data at a cloud storage server, and the data can be accessed by a group of users authorized by the data owner. As an example, the data owner could be an organization and the authorized users are the organization employees. Without fully trusting the cloud server, the data owner encrypts the data to ensure the security and privacy of the data. Here, data encryption serves as a measure of fine-grained access control, and users have different decryption capabilities based on the specified need-to-know basis. In particular, a user’s decryption capability is delineated by a set of attributes according to the user’s functional role. Each data encryption is associated with an access control policy (specified with respect to attributes), such that a user can successfully decipher the encrypted record, if, and only if, the user’s attributes satisfy the access policy. As the system is in a multi-user setting, user revocation is a critical requirement (e.g. when a user leaves the organization or is no longer involved in the project). User revocation would allow the data owner to revoke a user’s ability to decipher the data.
3.2 Notations
We use the definitions of “attribute” and “access structure” from [4, 13].
Attributes. Let \(\varLambda \) denotes the dictionary of descriptive attributes used in the system. Each authorized cloud storage user, u, is assigned with a set of attributes \(\mathbb {A}_u\subseteq \varLambda \), which defines the user’s functional role. The attribute assignment procedure is application specific and is beyond the scope of this paper.
Access Policy. In the system, an access control policy is expressed by an access tree, where each leaf node represents an attribute and we use att(\(\ell \)) to denote the attribute associated with leaf node \(\ell \). Each non-leaf node of the tree represents a threshold gate, described by its children and a threshold value. Let \(num_n\) be the number of children of a non-leaf node n, and \(t_n\) be its threshold value, where \(1\le t_n\le num_n\). When \(t_n=1\), the threshold gate is an OR gate, and when \(t_n = num_n\), it is an AND gate. The parent of a node n in the tree is denoted by parent(n). The tree also defines an ordering among the children of a node – i.e. the child nodes of a node n are numbered from 1 to \(num_n\). The function index(n) calculates the unique number associated with a node n. The access tree can express any access policy in the form of monotonic formula.
Satisfying an Access Tree. Let \(\mathcal {T}\) be an access tree with root rt. The subtree of \(\mathcal {T}\) rooted at node n is denoted as \(\mathcal {T}_n\); hence, \(\mathcal {T} = \mathcal {T}_{rt}\). When a set \(\mathbb {A}\) of attributes satisfy the access tree \(\mathcal {T}_n\), it is denoted as \(\mathcal {T}_n(\mathbb {A}) = 1\). \(\mathcal {T}_n(\mathbb {A})\) is computed in a recursive way as follows: if n is a non-leaf node, then compute \(\mathcal {T}_{n'}(\mathbb {A})\) for all child nodes \(n'\); \(\mathcal {T}_n(\mathbb {A})\) returns 1 if, and only if, at least \(t_n\) children return 1; if n is a leaf node, then \(\mathcal {T}_n(\mathbb {A})\) returns 1 if and only if att(n) \(\in \mathbb {A}\).
3.3 Extended Proxy-Assisted User Revocation Approach
To strengthen key revocation and to reduce the possibility of a dishonest cloud server, our approach requires the cloud server to use its own private key in the partial decryption phase. In other words, unless the cloud server is willing to disclose its private key, the exposure of a user’s cloud-side key (referred to as proxy key in this paper) to a third party (e.g. a foreign government agency) does not help in deciphering the encrypted cloud data. As our approach is an extension of the proxy-assisted approach, it inherits the advanced features of the latter, such as immediate user revocation, small amount of overhead for revocation, light computation cost for user side, and key escrow-free.
3.4 Formulation of Revocable Cloud Data Encryption
A revocable cloud data encryption system involves three types of entities, namely: data owner (denoted as DO), a set of users, and a cloud server (denoted as CS). Each user and CS have their respective public/private key pairs. To authorize a user, DO generates a proxy key based on the user’s attributes, the user’s public key, and CS’s public key; the proxy key is given to and held by CS. Therefore, CS maintains a Proxy Key list, with each entry containing a user’s identity and the corresponding proxy key. When a user requests to retrieve a data record from the cloud, CS executes a proxy decryption operation over the data with the user’s proxy key and its own private key to generate an intermediate value. The value is then returned to the user, who is able to obtain the underlying plain data by running a user decryption operation with his/her private key. Specifically, the system consists of the following algorithms.
Definition 1
Let \(\varLambda \) denote the universe of attributes. A revocable cloud data encryption system (RCDE) is defined as a collection of the following algorithms.
-
Setup \((1^\kappa )\rightarrow (params,msk)\) : Taking as input a security parameter \(1^\kappa \), DO executes the algorithm to set up public parameters, params, and a master secret key, msk. Below, we assume that params is implicit in the input of the rest algorithms unless stated otherwise.
-
UKGen \((u)\rightarrow (pk_u,sk_u)\) : The user key generation algorithm takes as input a user identity, u, and outputs a pair of public/private keys, \((pk_u\), \(sk_u)\), for u. Note that \((pk_u\), \(sk_u)\) is a pair for a standard public key cryptosystem.
Each system entity (including users and CS) runs this algorithm to generate a key pair. As \((pk_{\mathsf{CS}}\), \(sk_{\mathsf{CS}})\) – the key pair of CS –is a standard public key cryptosystem, we assume that \((pk_{\mathsf{CS}}\), \(sk_{\mathsf{CS}})\) is for long term use, and CS does not expose the private key, \(sk_{\mathsf{CS}}\).
-
PxKGen \((msk, pk_{CS}, pk_u, \mathbb {A}_u)\rightarrow PxK_u\) : The proxy key generation algorithm takes as input msk, the server’s public key, \(pk_{\mathsf{CS}}\), a user u’s public key, \(pk_u\), and the user’s attributes, \(\mathbb {A}_u\subset \varLambda \), and outputs a proxy key, \(PxK_u\), for u.
DO runs this algorithm to authorize a user based on the user’s attributes. The proxy key, \(PxK_u\), will be given to CS who adds a new entry in its Proxy Key list \(\mathcal {L}_{PxK}\) – i.e. \(\mathcal {L}_{PxK} = \mathcal {L}_{PxK}\cup \{u, PxK_u\}\).
-
Encrypt \((m, \mathcal {T})\rightarrow c\) : The encryption algorithm takes as input a message, m, and an access tree, \(\mathcal {T}\), specifying an access policy, and outputs a ciphertext, c, under \(\mathcal {T}\).
DO runs this algorithm to encrypt data to be uploaded to CS.
-
PxDec \((sk_{CS}, PxK_u, c)\rightarrow v\) : The proxy decryption algorithm takes as input CS’s private key, sk CS , a user’s proxy key, \(PxK_u\), and a ciphertext, c, and outputs an intermediate value, v.
The CS runs this algorithm to help a user, u, partially decrypt an encrypted record requested by the user with the corresponding proxy key.
-
UDec \((sk_u,v)\rightarrow m\) : The user decryption algorithm takes as input a user private key, \(sk_u\), and an intermediate value, v, and outputs a message, m.
An authorized user runs this algorithm to obtain the data with the intermediate value returned by CS and his/her private key.
-
Revoke \((u,\mathcal {L}_{PxK})\rightarrow \mathcal {L}'_{PxK}\) : Taking as input a user identity, u, and the Proxy Key list, \(\mathcal {L}_{PxK}\), the algorithm revokes u’s decryption capability by updating and outputting an updated Proxy Key list, \(\mathcal {L}'_{PxK}\).
Correctness. Correctness of the system stipulates that \(\mathtt{UDec}(sk_u\), \({\texttt {PxDec}}(sk_{\mathsf{CS}}\), \(PxK_u\), \(c)) = m\) if \(\mathcal {T}(\mathbb {A})=1\), for all \((pk_u\), \(sk_u) \leftarrow \mathtt{UKGen}(u)\), \(PxK_u\leftarrow \mathtt{PxKGen} (msk\), \(pk_{\mathsf{CS}}\), \(pk_u\), \(\mathbb {A})\) and \(c \leftarrow \mathtt{Encrypt}(m\), \(\mathcal {T})\), where (params, \(msk) \leftarrow \mathtt{Setup}(1^\kappa )\).
Remark. The separation of the algorithms, UKGen and PxKGen, highlights the distinction between our key-escrow-free approach and the mediated cryptography with key escrow. For the latter, the two algorithms are combined into one, which is executed by a single party (e.g., DO in our case).
Security Requirements. We define the security requirements for our system.
Data Privacy Against Cloud Server. The primary purpose of data encryption is to protect data privacy against CS. It guarantees that CS cannot learn any useful information about the data in its storage system even with the knowledge of all users’ proxy keys (as well as its own private key).
Definition 2
[Data Privacy Against Cloud Server] A revocable cloud data encryption system (RCDE) achieves data privacy against the cloud server if for any probabilistic polynomial time (PPT) adversary, the probability of the following game returns 1 is \(1/2 + \epsilon (\kappa )\), where \(\epsilon (.)\) is a negligible function with respect to the security parameter, \(\kappa \).
Setup. The game challenger runs the Setup algorithm, and returns params to the adversary.
Phase 1. The adversary generates its own pair of public/private keys, and gives the public key to the challenger. It then makes repeated queries to the proxy key generation oracle by querying sets of attributes \(\mathbb {A}_1, ..., \mathbb {A}_{q_1}\). For each query i, (1) the challenger runs the UKGen algorithm to get a user public/private key pair; (2) with the adversary’s public key, the user public key, and the attribute set \(\mathbb {A}_i\), the challenger runs the PxKGen algorithm to get a proxy key; (3) the challenger returns the proxy key along with the user public key to the adversary.
Challenge. The adversary submits two equal-length messages, \(m_0\) and \(m_1\), along with a challenge access tree, \(\mathcal {T}^*\). The challenger flips a random coin, b, runs the Encrypt algorithm on \(m_b\) and \(\mathcal {T}^*\), and returns the ciphertext, \(c^*\), to the adversary.
Phase 2. The adversary continues to make proxy key generation queries, and the challenger responds as in Phase 1.
Guess. The adversary outputs a guess, \(b'\), on b. If \(b'=b\), then the challenger returns 1; otherwise returns 0.
Data Privacy Against Users. From the perspective of access control over cloud data, a user should not be able to decrypt data beyond the user’s authorized access rights issued by DO. In particular, a collusion of a set of malicious users will not afford these users’ decryption capabilities beyond those authorized.
Definition 3
[Data Privacy against Users] A revocable cloud data encryption system (RCDE) achieves data privacy against users if for any PPT adversary, the probability of the following game returns 1 is \(1/2 + \epsilon (\kappa )\).
Setup. The challenger runs the Setup algorithm, and returns params to the adversary.
Phase 1. The adversary makes repeated queries to the proxy key generation oracle (PxKGen) by issuing sets of attributes, \(\mathbb {A}_1, ..., \mathbb {A}_{q_1}\). To respond the queries, the challenger first generates a public/private key pair as the CS’s key by executing the UKGen algorithm, and gives the key pair to the adversary; then for each query i, the challenger (1) first generates a user public/private key by executing the UKGen algorithm and gives the key pair to the adversary; (2) then generates a proxy key by executing the PxKGen algorithm upon the CS’s public key, and the user public key and \(\mathbb {A}_i\), and returns the resulting proxy key to the adversary.
Challenge. The adversary submits two equal-length messages, \(m_0\) and \(m_1\), along with an access tree, \(\mathcal {T}^*\), subjecting to a restriction that none of the \(\mathbb {A}\)’s satisfies \(\mathcal {T}^*\). The challenger flips a random coin, b, runs the Encrypt algorithm on \(m_b\) and \(\mathcal {T}^*\), and returns the ciphertext, \(c^*\), to the adversary.
Phase 2. The adversary continues to make proxy key generation queries by submitting attribute sets as in Phase 1, with the restriction that none of the attribute sets satisfies \(\mathcal {T}^*\).
Guess. The adversary outputs a guess, \(b'\), on b. If \(b'=b\), then the challenger returns 1; otherwise returns 0.
Remark. This definition depicts a stronger adversarial capability as it allows users to gain access to the cloud server’s key and the proxy keys.
User Revocation Support. The extended proxy-assisted user revocation approach guarantees that without knowing CS’s private key, any user cannot decipher encrypted data even given the corresponding proxy key (in addition to the user key pair).
Definition 4
[User Revocation Support] A revocable cloud data encryption system (RCDE) supports user revocation if for any PPT adversary, the probability of the following game returns 1 is \(1/2 + \epsilon (\kappa )\).
Setup. The challenger runs the Setup algorithm, and returns params to the adversary.
Phase 1. The challenger generates a public/private key pair as CS’s key by executing the UKGen algorithm, and gives the public key to the adversary. The adversary makes repeated queries to the proxy key generation oracle by issuing a set of attributes \(\mathbb {A}_1, ..., \mathbb {A}_{q_1}\). For each query i, the challenger (1) generates a user public/private key pair and gives the key pair to the adversary; (2) generates a proxy key by executing the PxKGen algorithm upon the CS’s public key, the user public key and \(\mathbb {A}_i\), and returns the resulting proxy key to the adversary.
Challenge. The adversary submits two equal-length messages, \(m_0\) and \(m_1\), along with an access tree, \(\mathcal {T}^*\). The challenger flips a random coin, b, runs the Encrypt algorithm on \(m_b\) and \(\mathcal {T}^*\), and returns the ciphertext, \(c^*\), to the adversary.
Phase 2. The adversary continues to make proxy key generation queries, as in Phase 1.
Guess. The adversary outputs a guess, \(b'\), on b. If \(b'=b\), the challenger returns 1; otherwise returns 0.
4 Our Construction
In this section, we present a concrete construction of our novel extended proxy-assisted user revocation approach described in Sect. 3. The construction is adapted from the CP-ABE scheme in [4], and it achieves the same expressiveness for access policy as in [4, 13]. We state that it is not difficult to extend the following construction idea to other ABE schemes with more expressive attributes, such as the scheme in [28].
4.1 Construction Details
The main challenge in our construction is the generation of a user’s proxy key by seamlessly incorporating the cloud server’s public key and the user’s public key into the decryption key generation algorithm of the CP-ABE scheme in [4]. Let \(s\in _R S\) denotes an element s randomly chosen from a set S. The details of our construction are described as follow.
-
Setup \((1^{\kappa })\) : On input a security parameter \(1^{\kappa }\), the algorithm: determines a bilinear map, \(e: G_0\times G_0 \rightarrow G_T\), where \(G_0\) and \(G_T\) are cyclic groups of \(\kappa \)-bit prime order p. Selects g, which is a generator of \(G_0\). Selects a cryptographic hash function, \(H:\{0,1\}^* \rightarrow G_0\). Picks \(\alpha , \beta \in _R Z_p\), and sets \(params = (e, G_0, g, h = g^{\beta }, \mathcal {G}_{\alpha } = e(g,g)^{\alpha })\) and \(msk = (\alpha , \beta )\).
-
UKGen(u): On input a user identity u, the algorithm chooses \(x_u \in _R Z_p\), and sets \((pk_u= g^{x_u}, sk_u = x_u)\). It can be seen that \((pk_u,sk_u)\) is a standard ElGamal type key pair. CS also uses this algorithm to generate a key pair, \((pk_{\mathsf{CS}} = g^{x_{\mathsf{CS}}}, sk_{\mathsf{CS}} = x_{\mathsf{CS}})\).
-
PxKGen \((msk, pk_{\mathsf{CS}}, pk_u, \mathbb {A}_u)\) : On input \(msk = (\alpha , \beta ), pk_{\mathsf{CS}} = g^{x_{\mathsf{CS}}}, pk_u = g^{x_u}\) and \(\mathbb {A}_u\), the algorithm chooses \(r_1, r_2, r_i \in _R Z_p, \forall i \in \mathbb {A}_u\), and sets \(PxK_u =(k=(pk_{\mathsf{CS}}^{r_1}pk_{u}^{\alpha }g^{r_2})^{\frac{1}{\beta }}, k' = g^{r_1}\) and \( \forall i\in \mathbb {A}_u: \{k_{i1} =g^{r_2}H(i)^{r_i}, k_{i2}=g^{r_i}\})\).
-
Encrypt \((m,\mathcal {T})\) : Taking as input a message, m, and \(\mathcal {T}\), the algorithm works as follows: Firstly, it selects a polynomial, \(q_n\), for each node, n, (including the leaf nodes) in \(\mathcal {T}\). These polynomials are chosen in a top-down manner starting from the root node, rt. For each node n, set the degree \(d_n\) of the polynomial \(q_n\) to be \(d_n = t_n-1\), where \(t_n\) is the threshold value of node n. Starting with the root node, rt, the algorithm chooses an \(s\in _R Z_p\), and sets \(q_{rt}(0) = s\). It next selects \(d_{rt}\) other random points to define \(q_{rt}\) completely. For any other node n, it sets \(q_n(0) = q_\mathsf{{parent}(n)}(\mathsf{index}(n))\), and chooses \(d_n\) other points to define \(q_n\). Let L be the set of leaf nodes in \(\mathcal {T}\). The algorithm sets the ciphertext, c, as \( c = (\mathcal {T}, C=m\cdot \mathcal {G}_{\alpha }^s, C'=h^s, C'' = g^s, \forall \ell \in L: \{C_{\ell 1} = g^{q_l(0)}, C_{\ell 2} = H(\mathsf{att}(\ell ))^{q_l(0)}\}) \).
-
PxDec \((sk_{\mathsf{CS}}, PxK_u, c)\) : On input \(sk_{\mathsf{CS}} = x_{\mathsf{CS}}\), and \(PxK_u = (k, k', \forall i\in \mathbb {A}_u: \{k_{i1}, k_{i2}\})\) associating with a set of attributes, \(\mathbb {A}_u\), and a ciphertext, \(c = (\mathcal {T}, C, C', C'', \forall \ell \in L: \{C_{\ell 1}, C_{\ell 2}\})\), the algorithm outputs an intermediate value, v if \(\mathcal {T}(\mathbb {A}_u)=1\), and \(\bot \) otherwise. Specifically, the algorithm is recursive. We first define an algorithm, DecNd \(_n(PxK_u, c)\), on a node, n, of \(\mathcal {T}\). If node, n, is a leaf node, we let \(z = \mathsf{att}(n)\) and define as follows: \(z \notin \mathbb {A}_u\), DecNd \(_n(PxK_u, c) = \bot \); otherwise DecNd \(_n(PxK_u, c) = F_n\), where \(F_n = \frac{e(k_{z1}, C_{n1})}{e(k_{z2},C_{n2})} = \frac{e(g^{r_2}H(z)^{r_z}, g^{q_n(0)})}{e(g^{r_z}, H(z)^{q_n(0)})} = e(g,g)^{r_2.q_n(0)}\).
We now consider the recursive case when n is a non-leaf node. The algorithm, DecNd \(_n(PxK_u, c)\), then works as follows. For each child node ch of n, it calls DecNd \(_{ch}(PxK_u, c)\), and stores the output as \(F_{ch}\). Let \(S_n\) be an arbitrary \(t_n\)-sized set of child nodes, ch, such that \(F_{ch} \ne \bot \). If such a set does not exist, then the node is not satisfied and \(\mathsf{DecNd}_n(PxK_u,c) = F_n =\bot \). Otherwise, we let the Lagrange coefficient, \(\bigtriangleup _{i,S}\) for \(i\in Z_p\), and a set S of elements in \(Z_p\) be \(\bigtriangleup _{i,S}(x) = \prod _{j\in S,j\ne i}\frac{x-j}{i-j}\). We next compute

In this way, DecNd \(_{rt}(PxK_u, c)\) for the root node rt can be computed if \(\mathcal {T}_{rt}(\mathbb {A}_u)=1\), where DecNd \(_{rt}(PxK_u, c)=e(g,g)^{r_2.q_{rt}(0)} = e(g,g)^{r_2.s} = F_{rt}\). Next, the proxy decryption algorithm computes
$$\begin{aligned} \frac{e(k, C')}{e(k', C'')^{x_{\mathsf{CS}}}F_{rt}} = \frac{e((pk_{\mathsf{CS}}^{r_1}pk_u^{\alpha }g^{r_2})^{\frac{1}{\beta }}, h^s)}{e(g^{r_1}, g^s)^{x_{\mathsf{CS}}}e(g,g)^{r_2.s}} = e(pk_u, g)^{s.\alpha }. \end{aligned}$$Finally, it sets \(v = (C=m\cdot \mathcal {G}_{\alpha }^s, e(pk_u, g)^{s.\alpha })\).
-
UDec \((sk_u, v)\) : On input a user private key, \(sk_u = x_u\), and an intermediate value, \(v = (C=m\cdot \mathcal {G}_{\alpha }^s, e(pk_u, g)^{s.\alpha })\), the user decryption algorithm computes \(\frac{m\cdot \mathcal {G}_{\alpha }^s}{(e(pk_u, g)^{s.\alpha })^{x_u^{-1}}} = m\).
-
Revoke \((u,\mathcal {L}_{PxK})\) : On input a user identity, u, and the Proxy Key list, \(\mathcal {L}_{PxK}\), the user revoking algorithm deletes the entry corresponding to u from the list – i.e. \(\mathcal {L}'_{PxK} = \mathcal {L}_{PxK}\setminus \{u, PxK_u\}\). In a real world application, an interface should be provided to DO for DO to perform the updating in real-time.
4.2 Functional Analysis – Features
Our construction enjoys a number of features as described below.
Efficient and Immediate User Revocation. The only overhead incurred due to user revocation is the deletion of the revoked user’s proxy key from the cloud server. Once the proxy key of a user is eliminated, the cloud server is no longer able to perform the proxy decryption for the revoked user.
Mitigation against Cloud-User Collusion. The primary purpose of the extended proxy-assisted user revocation is to reduce the likelihood of proxy keys disclosure (e.g. the cloud server may collude with some revoked users to reveal their proxy keys). In our construction, the leakage of a proxy key does not lead to the success of proxy decryption.
We note that there exists another way of colluding to invalidate user revocation. More specifically, the cloud server keeps a copy of a revoked user’s proxy key before it is deleted by the data owner, and then continues to service the revoked user’s data access with the retained proxy key. Unfortunately, such collusion cannot be prevented by any proxy/mediator based system. However, it is not difficult to detect collusion of this nature in practice (compared to the proxy keys disclosure collusion), as it requires ongoing engagement of the cloud server.
Free of Key Escrow. Each user generates its own key pair, and the data owner generating each authorized user’s proxy key does not need to know the user’s private key.
Cloud Transparency. Although the cloud server’s key is involved in the authorized users’ proxy keys, encrypting data only needs the access policy associated with the data to be encrypted, without the need to involve the cloud server. In other words, data encryption works as a regular CP-ABE encryption algorithm.
Minimal User Side Overhead. The bit-length of an intermediate value, v, output by the algorithm, PxDec, is \(2|G_T|\), independent of the complexity of access policy. In addition, the main computation overhead of the algorithm, UDec, includes just a single exponentiation in \(G_T\) (unlike \(G_0\), \(G_T\) is a regular finite field) without any bilinear pairing operation. Thus, the complexity overhead at the user side is relatively low in terms of both communication and computation.
No User Authentication. The cloud server is not require to check the authenticity of a requesting user, as the intermediate value output by the proxy decryption algorithm can only be decrypted by the user being impersonated (i.e. the impersonator will not be able to decrypt the intermediate value output).
4.3 Security Analysis
We have the following theorem asserting the security of our construction, and the security proof is deferred to the Appendix.
Theorem 1
Our construction is a revocable cloud data encryption system achieving Data Privacy Against Cloud Server (in the sense of Definition 2), Data Privacy Against Users (in the sense of Definition 3), and User Revocation Support (in the sense of Definition 4), in the generic group model [25].
5 Implementation of Our Construction
5.1 Proof-of-Concept
To demonstrate the practicality of the construction described in Sect. 4, we present a Web-based proof-of-concept.
Architecture. The prototype consists of a Web application representing a cloud server (running the algorithm PxDec), a data owner application, and a user application running the algorithm UDec. The data owner application takes charge of the algorithms Setup, PxKGen and Encrypt. A cloud-data-owner interface is provided, allowing the data owner application to upload encrypted data to the Web server. A cloud-user interface is also provided for the user to access and download data from the Web server. The Web server runs on a desktop with 2.66 GHz Intel Core2Duo and 3.25 GB RAM, the data owner application runs on a laptop with 2.10 GHz Intel Core i3-5010U Processor and 4 GB RAM, and the user application runs on a smartphone configured with a 1.2 GHz CPU and 2 GB RAM.
The implementation is based on the Pairing-Based Cryptography (PBC) library (https://crypto.stanford.edu/pbc/). The bilinear map in our construction is instantiated with a 512-bit supersingular curve of embedding degree 2, with \(|p|=160\). For the cryptographic hash function \(H:\{0,1\}^*\rightarrow G_0\), a simplified realization of choosing random values from \(G_0\) is used, as there is no off-the-shelf hash function of this nature. The data encryption follows the common practice of data encapsulation + key encapsulation, namely, an encryption of a message, m, is of the form \((\text {AES}_k(m), \mathsf{Encrypt}(k, \mathcal {T}))\), where k is a random encryption key. To achieve the security level guaranteed by the 512-bit supersingular curve, 128-bit AES is chosen. Since \(G_T\) is an ordinary finite field, the AES keys can be directly encrypted by the algorithm Encrypt.
Reducing Storage Overhead. In the prototype, we are concerned with reducing the storage overhead. Recall that the ciphertext size in our construction is linear with the number of leaf nodes in a given access tree - for a payload message \(m \in G_T\), a ciphertext introduces an extra storage overhead of \(2+2\ell \) group of elements in \(G_0\), where \(\ell \) is the total number of leaf nodes of the access tree. When \(\ell \) is large, the complexity overhead dominates the storage cost.
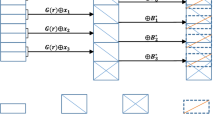
The mode of hybrid data/key encapsulation offers us a possibility to amortize the above complexity overhead. Specifically, all data sharing the same access policy are encrypted with the same encryption key. The high ciphertext overhead resulting from the encapsulation of the encryption key by the algorithm Encrypt is amortized by all these data. Note that the data owner is not necessarily involved in the management of the encryption keys. Instead, the data owner can obtain the key by retrieving and decrypting the corresponding ciphertext from the cloud server, if the access policy has already been used. We also remark that the decryption process by the data owner is very simple. With \(\alpha \), the data owner only needs to retrieve the \(C,C''\) elements of the ciphertext, and computes \(\frac{C}{e(g^{\alpha }, C'')}\) to recover the encryption key. If the data owner chooses to keep \(g^{\alpha }\) as a part of the master secret key, msk, the computation overhead is a single pairing operation. Figure 1 illustrates the logical structure of encrypted data records, where each ciphertext of the algorithm Encrypt serves as an index, pointing to all encrypted payload data that are governed by the same access policy.
The role played by this overhead amortization mechanism in user revocation is as follows. Once a user is revoked, the data owner will use a new key for every access policy when encrypting new data. This guarantees that the newly generated cloud data cannot be decrypted by the revoked user even if it is given the corresponding payload part. In practice, it is usually not a concern that a revoked user can decrypt the data it has been entitled to before its revocation.
5.2 Performance Results
We evaluated the performance of PxKGen, Encrypt, PxDec, and UDec, respectively, on their corresponding platforms. The experimental results are shown in Fig. 2. As observed in Fig. 2(a) and (b), the runtimes of the algorithms, PxKGen and Encrypt, are linear to the number of attributes. In our implementation, we had not undertaken any optimization on multi-exponentiation operations; therefore, the runtime of PxKGen is slightly more costly than that of Encrypt given the same number of attributes.
We experiment the algorithm, PxDec, with two types of access policies. The first type consists of access trees whose non-leaf nodes are all “and” gates (we call them all-and access trees). Access trees in such a form ensure that all attributes (leaf nodes) are needed in PxDec. Thus, the access trees are expected to impose the heaviest workload, among access trees with the same number of leaf nodes. The second type includes access trees that are constructed randomly (we call them random access trees). It is clear that for a random access tree whose non-leaf nodes are “or” or “threshold” gates, not all of the leaf nodes are necessary in order to satisfy the tree. The actual leaf nodes needed in PxDec are tree-specific. Figure 2(c) corroborates this fact. In the case of all-and access trees, the computation overhead is basically linear with the number of leaf nodes. It can also be seen that PxDec is more efficient than Encrypt given the same number of attributes (i.e. the same access tree). This is because the former is dominated by the exponentiation operations in \(G_T\), whereas the latter is dominated by the exponentiations in \(G_0\).
Figure 2(d) shows that a UDec operation costs about 80 milliseconds on the experimenting smartphone platform. Considering in addition that the communication overhead for user is merely \(2|G_T| = 1\) K bits in our implementation, this could be deployed on a smart mobile device (e.g. Android or iOS device).
6 Conclusion
In this paper, we presented an extended proxy-assisted approach in order to overcome the limitation of needing to trust the cloud server not to disclose users’ proxy keys inherent in proxy/mediator assisted user revocation approaches. In our approach, we bind the cloud server’s private key to the data decryption operation, which requires the cloud server to reveal its private key should the cloud server decide to collude with revoked users. We then formulated a primitive, ‘revocable cloud data encryption’, under the approach. We presented a concrete construction of the primitive and implemented the construction using a proof-of-concept. The experimental results suggested that our construction is suitable for deployment even on smart mobile devices.
References
Attrapadung, N., Imai, H.: Attribute-based encryption supporting direct/indirect revocation modes. In: Parker, M.G. (ed.) Cryptography and Coding 2009. LNCS, vol. 5921, pp. 278–300. Springer, Heidelberg (2009)
Blaze, M., Bleumer, G., Strauss, M.: Divertible protocols and atomic proxy cryptography. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 127–144. Springer, Heidelberg (1998)
Boneh, D., Ding, X., Tsudik, G., Wong, C.M.: A method for fast revocation of public key certificates and security capabilities. In: Proceedings of USENIX Security (2001)
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: Proceedings of IEEE S&P, pp. 321–334 (2007)
Choo, K.K.R.: Legal issues in the cloud. IEEE Cloud Comput. 1(1), 94–96 (2014)
Chow, S.S.M., Boyd, C., González Nieto, J.M.: Security-mediated certificateless cryptography. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T. (eds.) PKC 2006. LNCS, vol. 3958, pp. 508–524. Springer, Heidelberg (2006)
Chen, Y., Jiang, L., Yiu, S., Au, M., Xuan, W.: Fully-RCCA-CCA-Secure ciphertext-policy attribute based encryption with security mediator. In: Proceedings of ICICS 2014 (2014)
Cloud Security Alliance: Security guidance for critical areas of focus in cloud computing (2009). http://www.cloudsecurityalliance.org
Chu, C.-K., Zhu, W.T., Han, J., Liu, J.K., Xu, J., Zhou, J.: Security concerns in popular cloud storage services. IEEE Pervasive Comput. 12(4), 50–57 (2013)
European Network and Information Security Agency: Cloud computing risk assessment (2009). http://www.enisa.europa.eu/act/rm/files/deliverables/cloud-computing-risk-assessment
Gartner: Don’t trust cloud provider to protect your corporate assets, 28 May 2012. http://www.mis-asia.com/resource/cloud-computing/gartner-dont-trust-cloud-provider-to-protect-your-corporate-assets
Green, M., Hohenberger, S., Waters, B.: Outsourcing the decryption of ABE ciphertexts. In: Proceedings of USENIX Security (2011)
Goyal, V., Pandy, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Proceedings of ACM CCS 2006, pp. 89–98 (2006)
Hohenberger, S., Waters, B.: Online/offline attribute-based encryption. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 293–310. Springer, Heidelberg (2014)
Jiang, T., Chen, X., Li, J., Wong, D.S., Ma, J., Liu, J.: TIMER: secure and reliable cloud storage against data re-outsourcing. In: Huang, X., Zhou, J. (eds.) ISPEC 2014. LNCS, vol. 8434, pp. 346–358. Springer, Heidelberg (2014)
Liang, K., Au, M.H., Liu, J.K., Susilo, W., Wong, D.S., Yang, G., Phuong, T.V.X., Xie, Q.: A DFA-based functional proxy pe-encryption scheme for secure public cloud data sharing. IEEE Trans. Inf. Forensics Secur. 9(10), 1667–1680 (2014)
Liang, K., Liu, J.K., Wong, D.S., Susilo, W.: GO-ABE: an efficient cloud-based revocable identity-based proxy re-encryption scheme for public clouds data sharing. In: Proceedings of ESORICS 2014, pp. 257-272 (2014)
Liang, K., Susilo, W., Liu, J.K.: Privacy-preserving ciphertext multi-sharing control for big data storage. IEEE Trans. Inf. Forensics Secur. 10(8), 1578–1589 (2015)
Liu, J.K., Au, M.H., Susilo, W., Liang, K., Lu, R., Srinivasan, B.: Secure sharing and searching for real-time video data in mobile cloud. IEEE Netw. 29(2), 46–50 (2015)
Li, M., Huang, X., Liu, J.K., Xu, L.: GO-ABE: group-oriented attribute-based encryption. In: Au, M.H., Carminati, B., Kuo, C.-C.J. (eds.) NSS 2014. LNCS, vol. 8792, pp. 260–270. Springer, Heidelberg (2014)
Liu, Z., Wong, D.S.: Practical attribute based encryption: traitor tracing, revocation, and large universe. https://eprint.iacr.org/2014/616.pdf
Naor, D., Naor, M., Lotspiech, J.: Revocation and tracing schemes for stateless receivers. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 41–62. Springer, Heidelberg (2001)
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Proceedings of ACM CCS 2007, pp. 195–203 (2007)
Quick, D., Martini, B., Choo, K.K.R.: Cloud Storage Forensics. Syngress/Elsevier, Amsterdam (2014)
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997)
Sahai, A., Seyalioglu, H., Waters, B.: Dynamic credentials and ciphertext delegation for attribute-based encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 199–217. Springer, Heidelberg (2012)
Schwartz, J.T.: Fast probabilistic algorithms for verification of polynomial identities. J. ACM 27(4), 701–717 (1980)
Waters, B.: Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 53–70. Springer, Heidelberg (2011)
Wang, G., Liu, Q., Wu, J.: Hierarhical attribute-based encryption for fine-grained access control in cloud storage services. In: Proceedings of ACM CCS 2010, pp. 735–737 (2010)
Yang, K., Jia, X.: Expressive, efficient, and revocable data access control for multiauthority cloud storage. IEEE Trans. Parallel Distrib. Syst. 25(7), 1735–1744 (2014)
Yang, K., Jia, X., Ren, K., Zhang, B., Xie, R.: DAC-MACS: effective data access control for multiauthority cloud storage systems. IEEE Trans. Inf. Forensics Secur. 8(11), 1790–1801 (2013)
Yang, Y., Ding, X., Lu, H., Wan, Z., Zhou, J.: Achieving revocable fine-grained cryptographic access control over cloud data. In: Proceedings of ISC 2013 (2013)
Yang, Y., Lu, H., Weng, J., Zhang, Y., Sakurai, K.: Fine-grained conditional proxy re-encryption and application. In: Chow, S.S.M., Liu, J.K., Hui, L.C.K., Yiu, S.M. (eds.) ProvSec 2014. LNCS, vol. 8782, pp. 206–222. Springer, Heidelberg (2014). Extended version to appear: Pervasive and Mobile Computing, ELSEVIER
Yu, S., Wang, C., Ren, K., Lou, W.: Achieving secure, scalable, and fine-grained aata access control in cloud computing. In: Proceedings of IEEE INFOCOM 2010 (2010)
Yuen, T.H., Zhang, Y., Yiu, S.M., Liu, J.K.: Identity-based encryption with post-challenge auxiliary inputs for secure cloud applications and sensor networks. In: Kutyłowski, M., Vaidya, J. (eds.) ICAIS 2014, Part I. LNCS, vol. 8712, pp. 130–147. Springer, Heidelberg (2014)
Zippel, R.: Probabilistic algorithms for sparse polynomials. In: Ng, K.W. (ed.) EUROSAM/ISSAC 1979. LNCS, vol. 72, pp. 216–226. Springer, Heidelberg (1979)
Acknowledgment
Joseph K. Liu is supported by National Natural Science Foundation of China (61472083). Kaitai Liang is supported by privacy-aware retrieval and modelling of genomic data (PRIGENDA, No. 13283250), the Academy of Finland.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Security Proof for Theorem 1
Appendix: Security Proof for Theorem 1
Proof
We prove that our construction satisfies the three security requirements.
Lemma 1
The construction satisfies Data Privacy Against Cloud, as defined in Definition 2 in the generic group model.
Proof
In the definition, the attributes, \(\mathbb {A}_i\), submitted by the adversary could or could not satisfy the challenge access tree \(\mathcal {T}^*\). To consider the strongest adversary possible, we assume every \(\mathbb {A}_i\) satisfy \(\mathcal {T}^*\). We then prove under the generic group model, no efficient adversary can output \(b'=b\) in the security game defined in Definition 2 noticeably better than a random guess. Note that a random guess, \(b'\), by the adversary equals b with probability 1/2, thus we often call \(\epsilon \) the advantage of the adversary if \(b'=b\) with probability \(1/2+\epsilon \).
In the generic group model [25], each element of groups, \(G_0, G_T\), is encoded as a unique random string; thus, the adversary can directly test no properties other than equality. The opaque encoding of the elements in \(G_0\) is defined as the function \(\xi _0: Z_p\rightarrow \{0,1\}^*\), which maps all \(a\in Z_p\) to the string representation \(\xi _0(a)\) of \(g^a\in G\). Likewise, \(\xi _T:Z_p\rightarrow \{0,1\}^*\) maps \(a\in Z_p\) to the string representation \(\xi _T(a)\) of \(e(g,g)^a\in G_T\). The adversary communicates with the oracles to perform group action on \(G_0,G_T\) and bilinear map \(e:G_0\times G_0\rightarrow G_T\), by way of the \(\xi _0\)-representation and \(\xi _T\)-representation only.
For simplicity, the original game is slightly modified: in the challenge phase of the original security game, the adversary is given a challenge ciphertext, whose C component is either \(m_0\cdot e(g,g)^{\alpha \cdot s}\) or \(m_1\cdot e(g,g)^{\alpha \cdot s}\). We modify C to be either \(e(g,g)^{\alpha \cdot s}\) or \(e(g,g)^{\vartheta }\), for a random \(\vartheta \) in \(Z_p\). Indeed, any adversary that has a advantage \(\epsilon \) in the original game can be transformed into an adversary having advantage \(\epsilon /2\) in the modified game (consider two hybrids: one in which the adversary is to distinguish between \(m_0\cdot e(g,g)^{\alpha \cdot s}, e(g,g)^{\vartheta })\), and the other in which the adversary is to distinguish between \(m_1\cdot e(g,g)^{\alpha \cdot s}\) and \(e(g,g)^{\vartheta }\).
Hereafter, we consider the adversary in the modified game. In the Setup phase, the challenger sends the public parameters \(\xi _0(1), \xi _0(\beta ), \xi _T(\alpha )\) to the adversary. To simulate the hash function H, the challenger maintains a table, which is initially empty. Whenever a query i is asked on H, if i has never been asked before, the challenger selects a random value \(t_i\in _R Z_p\), and adds an entry \((i, t_i, \xi _0(t_i))\) to the table and returns \(\xi _0(t_i)\); otherwise, returns the already defined \(\xi _0(t_i)\).
In Phase 1, the adversary starts by selecting \(x\in _R Z_p\) and getting \(\xi _0(x)\) from the challenger. Then, the adversary makes a set of proxy key generation queries. For a jth query \(\mathbb {A}_j\), the challenger first picks \(x_j\in _R Z_p\) and computes \(\xi _0(x_j)\). Then the challenger picks \(r_1, r_2, r_i\in _R Z_p\) for all \(i\in \mathbb {A}_j\), and sets \(PxK_j = (k = \xi _0(\frac{r_1\cdot x+x_j\cdot \alpha +r_2}{\beta }), k' = \xi _0(r_i), \forall i\in \mathbb {A}_j: \{k_{i1}=\xi _0(r_2+t_i\cdot r_i), k_{i2}=\xi _0(r_i)\})\), where \(t_i\) is obtained by querying i upon the random oracle H as described above. Finally, the challenger gives \(\xi _0(t_i), \xi _0(x_j)\) and \(PxK_j\) to the adversary.
In the Challenge phase, the adversary submits two equal-length challenge messages \(m_0,m_1\) and a challenge access tree \(\mathcal {T}^*\). The challenger responds as follows. Select \(s\in _R Z_p\), and compute shares \(\varsigma _i\) of s for each attribute i contained in \(\mathcal {T}^*\) (represented by \(\mathcal {T}\)’s leaf nodes) along the tree as described in the Encryp algorithm. Note that \(\varsigma _i\)’s are random values subject to the underlying secret sharing induced by \(\mathcal {T}^*\). Finally, the challenger chooses \(\vartheta \in _R Z_p\), and returns to the adversary the challenge ciphertext \(c^*\) as \(C = \xi _T(\vartheta ), C' = \xi _0(\beta \cdot s), C''=\xi _0(s)\), and \(C_{i1} =\xi _0(\varsigma _i),C_{i2} =\xi _0(t_i\cdot \varsigma _i)\) for each attribute i in \(\mathcal {T}^*\).
In Phase 2, the challenger responds to the proxy key generation queries from the adversary, just as in Phase 1.
Analysis of the Simulated Game. Let q bound the total number of group elements the adversary receives during the game from the queries it makes to the oracles for \(G_0,G_T\), the bilinear map, and the hash function (including the hash function queries implicitly invoked by the proxy key generation and the challenge ciphertext generation). We will show that with probability \(1-\mathcal {O}(q^2/p)\), the adversary’s view in this simulated game is identically distributed to what its view could be if it has been given \(C=\xi _T(\alpha \cdot s)\) in the game. Note that in the current game, the adversary’s advantage is 0, as \(\xi _T(\vartheta )\) is independent of the encryption of the challenge messages. We thus conclude that the advantage of the adversary, when given \(C=\xi _T(\alpha \cdot s)\), is at most \(\mathcal {O}(q^2/p)\), which proves the theorem if \(q^2/p\) is negligible.
We assume that the adversary communicates with group oracles, only with values it has already received from the oracles. Note that each query the adversary makes is of the form of a rational function \(\pi = \chi /\gamma \) in the variables of \(\alpha , \beta , x, x^{[j]}, r_1^{[j]}, r_2^{[j]}, t_i,r^{[j]}_i, s\), and \(\varsigma _i\), where the subscript variable i denotes the attribute strings and the superscript variable [j] is the index of the proxy key queries. We now place a condition on the event that no “unexpected collisions” occur in either \(G_0\) and \(G_T\). An unexpected collision is one when two queries of two distinct rational functions \(\chi /\gamma \ne \chi '/\gamma '\) coincide in value, due to the random choices of the values of the involved variables. For any pair of queries corresponding to \(\chi /\gamma \) and \(\chi '/\gamma '\), a collision occurs only if the non-zero polynomial \(\chi /\gamma - \chi '/\gamma '\) evaluates to be zero. In our case, the degree of \(\chi /\gamma - \chi '/\gamma '\) is a small number; thus, the probability of a collision is \(\mathcal {O}(1/p)\) [27, 36]. By a union bound, the probability of any unexpected collision happens is at most \(\mathcal {O}(q^2/p)\) for q queries. As a result, we have probability \(1-\mathcal {O}(q^2/p)\) that no unexpected collisions happen.
Subject to the condition of no unexpected collisions, we need to show that the adversary’s view is identically distributed if the challenger has set \(\vartheta = \alpha \cdot s\). The view of the adversary can differ in the case of \(\vartheta = \alpha \cdot s\) only if there are two queries \(\pi ,\pi '\) into \(G_T\), such that \(\pi \ne \pi '\) but \(\pi \mid _{\vartheta =\alpha \cdot s}=\pi '\mid _{\vartheta =\alpha \cdot s}\). We will show that this will not happen.
Recall that \(\vartheta \) only occurs as \(\xi _T(\vartheta )\), which is an element of \(G_T\). Thus, the only difference that \(\pi \) and \(\pi '\) can have on \(\vartheta \) is such that \(\pi -\pi '=\eta \vartheta -\eta \alpha \cdot s\), for a constant \(\eta \). It suffices to show that the adversary can never construct a query for \(\xi _T(\eta \alpha \cdot s=\pi -\pi '+\eta \vartheta )\), given that no unexpected collisions occur. This reaches a contradiction and establishes the theorem.
This follows from the following analysis, based on the information given to the adversary during the game. For ease of reference, Table 1 enumerates all rational functions in \(G_0\) known to the adversary by means of the system setup, proxy key generation queries and challenge ciphertext query (\(i,i'\) are possible attribute strings, and j is the index of the proxy key generation queries). In addition, the adversary also knows the value of x (which represents the cloud server’s key). Any query in \(G_T\) is a linear combination of products of pairs of these rational functions (of course, x or \(\frac{1}{x}\) can be the coefficients, as the adversary knows the value of x). Observe from the table that the only rational function containing \(\alpha \) is \(\frac{r_1^{[j]}\cdot x+ x^{[j]}\cdot \alpha +r_2^{[j]}}{\beta }\). In order for the adversary to produce a rational function containing \(\eta \alpha \cdot s\), while at the same time canceling out other elements as much as possible, the only choice is multiplying \(\frac{r_1^{[j]}\cdot x+ x^{[j]}\cdot \alpha +r_2^{[j]}}{\beta }\) and \(\beta \cdot s\). This will create a polynomial of the form \(r_1^{[j]}\cdot x\cdot s + x^{[j]}\cdot \alpha \cdot s + r_2^{[j]}\cdot s\) (for simplicity, we always omit constant coefficients whenever possible). It is easy to cancel out the term \(r_1^{[j]}\cdot x\cdot s\) by multiplying \(r_1^{[j]}\) and s, together with the knowledge of x. Now, we have a polynomial \(x^{[j]}\cdot \alpha \cdot s + r_2^{[j]}\cdot s\), and we need to eliminate the term \(r_2^{[j]}\cdot s\). There are two options: (1) Multiplying \(r_2^{[j]} + t_i\cdot r_i^{[j]}\) and s introduces an additional term \(t_i\cdot r_i^{[j]}\cdot s\). This additional term can be canceled out only by an appropriate combination of the products of \(t_{i'}\cdot \varsigma _{i'}\) and s, following the secret sharing induced by \(\mathcal {T}^*\). We are eventually left with the term \(x^{[j]}\cdot \alpha \cdot s\). To construct a query for \(\xi _T(\eta \alpha \cdot s)\) where \(\eta \) is a constant known to the adversary, we must cancel out \(x^{[j]}\) from \(x^{[j]}\cdot \alpha \cdot s\). This is not possible using any combination of the rational functions in Table 1, as long as the adversary does not know \(x^{[j]}\) and \(\frac{1}{x^{[j]}}\). (2) Multiplying \(r_2^{[j]} + t_i\cdot r_i^{[j]}\) and \(\varsigma _{i'}\), which eventually leads to the canceling out of \(r_2^{[j]}\cdot s\) and other introduced terms (following the secret sharing induced by \(\mathcal {T}^*\)) as desired. But again, we need to cancel out \(x^{[j]}\) from \(x^{[j]}\cdot \alpha \cdot s\), as in the first case. This completes the proof. \(\square \)
Lemma 2
The construction satisfies Data Privacy Against Users as defined in Definition 3, if the CP-ABE scheme in [4] is CPA secure.
Proof
We prove that an adversary \(\mathcal {A}\) to our scheme can be transformed to an adversary \(\mathcal {B}\) to the CP-ABE scheme [4] which is proven secure in the generic group model. The construction of \(\mathcal {B}\) is by means of invoking \(\mathcal {A}\), with the help of its own chosen plaintext attack (CPA) game in terms of the CP-ABE scheme. In particular, \(\mathcal {B}\) has to answer \(\mathcal {A}\)’s proxy key generation queries. We show that within the context of the CPA game between \(\mathcal {B}\) and its own challenger, \(\mathcal {B}\) can answer \(\mathcal {A}\)’s proxy key generation queries, simulating \(\mathcal {A}\)’s challenger.
Specifically, when the CPA game between \(\mathcal {B}\) and its challenger starts, \(\mathcal {B}\) starts the Setup phase with \(\mathcal {A}\) by passing the public system parameters it gets from its own challenger (we do not consider the delegate functionality in [4]). In Phase 1, \(\mathcal {B}\) first generates \((g^x, x\in _R Z_p)\) as the cloud server’s key pair. When receiving an attribute set \(\mathbb {A}\) from \(\mathcal {A}\) as jth proxy key generation query, \(\mathcal {B}\) first makes a key generation (KeyGen in [4]) query on \(\mathbb {A}\) to its own challenger, and upon it, \(\mathcal {B}\) gets a decryption key of the form \((k = g^{\frac{\alpha +r_2}{\beta }}, \{k_{i1} = g^{r_2}H(i)^{r_i}, k_{i2}=g^{r_i}\}_{i\in \mathbb {A}})\) (having been collated with the notations in our construction). The challenge of the simulation is how to derive a valid proxy key for \(\mathcal {A}\) from the decryption key. To this end, \(\mathcal {B}\) generates \((g^{x_j}, x_j\in _R Z_p)\) as the user key pair; then picks \(r_1\in _R Z_p\), and computes \(k = k^{x_j} = g^{\frac{\alpha \cdot x_j +r_2\cdot x_j}{\beta }}, k' = g^{r_1}, \forall i\in \mathbb {A}: k_{i1}=k_{i1}^{x_j}\cdot g^{-xr_1} = g^{r_2\cdot x_j-xr_1}H(i)^{r_i\cdot x_j}, k_{i2} = k_{i2}^{x_j} = g^{r_i\cdot x_j}\), and the proxy key is set to be \((k, k',\{k_{i1}, k_{i2}\}_{i\in \mathbb {A}})\). It remains to see that this is a valid proxy key. Note that \(k = g^{\frac{\alpha \cdot x_j +r_2\cdot x_j}{\beta }} = g^{\frac{xr_1 + \alpha \cdot x_j +r_2\cdot x_j-xr_1}{\beta }} = ((g^x)^{r_1}(g^{x_j})^{\alpha }g^{r_2\cdot x_j-xr_1})^{\frac{1}{\beta }}\). Hence \((k, k',\{k_{i1}, k_{i2}\}_{i\in {\mathbb {A}}})\) is indeed a valid proxy key, with “\(r_2\)” being \(r_2\cdot x_j-xr_1\) and “\(r_i\)” being \(r_i\cdot x_j\).
In Challenge phase, when \(\mathcal {A}\) submits \(m_0, m_1\) and \(\mathcal {T}^*\), \(\mathcal {B}\) submits them to its own challenger. As a response, \(\mathcal {B}\) gets a challenge ciphertext of the form \((\mathcal {T}^*, C=m_{b}\cdot \mathcal {G}_{\alpha }^s, C'=h^s, \forall \ell \in L: \{C_{\ell 1} = g^{q_l(0)}, C_{\ell 2} = H(\mathsf{att}(\ell ))^{q_l(0)}\})\) according to the encryption algorithm (i.e. Encrypt) in [4]. Note that this ciphertext is of the same format as in our construction, except that it does not have the \(C'' = g^s\) element in our construction. Fortunately, \(g^s\) actually can be computed from \(\forall \ell \in L: \{C_{\ell 1} = g^{q_l(0)}\}\), following the secret sharing induced by \(\mathcal {T}^*\).
In Phase 2, \(\mathcal {B}\) answers \(\mathcal {A}\)’s proxy key generation queries as in Phase 1. Finally, \(\mathcal {B}\) outputs whatever bit \(\mathcal {A}\) outputs. It can be seen that the simulation by \(\mathcal {B}\) is perfect. This completes the proof. \(\square \)
Lemma 3
The construction satisfies User Revocation Support as defined in Definition 4.
Proof
The proof will in general proceed in a similar way as in the proof for Lemma 1. The main difference is that in this proof, the adversary knows the value of \(x^{[j]}\)’s, instead of x. This results in the effect that it cannot cancel out the term \(r_1^{[j]}\cdot x\cdot s\) from the polynomial \(r_1^{[j]}\cdot x\cdot s + x^{[j]}\cdot \alpha \cdot s + r_2^{[j]}\cdot s\). To avoid repetition, we omit the details. \(\square \)
Combining the proofs for the above three lemmas, we complete the proof of Theorem 1. \(\blacksquare \)
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Yang, Y., Liu, J.K., Liang, K., Choo, KK.R., Zhou, J. (2015). Extended Proxy-Assisted Approach: Achieving Revocable Fine-Grained Encryption of Cloud Data. In: Pernul, G., Y A Ryan, P., Weippl, E. (eds) Computer Security -- ESORICS 2015. ESORICS 2015. Lecture Notes in Computer Science(), vol 9327. Springer, Cham. https://doi.org/10.1007/978-3-319-24177-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-24177-7_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-24176-0
Online ISBN: 978-3-319-24177-7
eBook Packages: Computer ScienceComputer Science (R0)