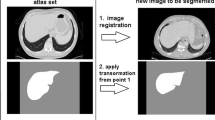
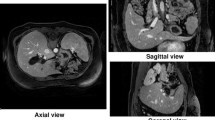
Abstract
An atlas is a shape model derived using statistics of a population. Standard models treat local deformations as pure translations and apply linear statistics. They are often inadequate for highly variable anatomical shapes. Non-linear methods has been developed but are generally difficult to implement.
This paper proposes encoding shapes using the special Euclidean group \(\mathbb{SE}(3)\) for model construction. \(\mathbb{SE}(3)\) is a Lie group, so basic linear algebra can be used to analyze data in non-linear higher-dimensional spaces. This group represents non-linear shape variations by decomposing piecewise-local deformations into rotational and translational components.
The method was applied to 49 human liver models that were derived from CT scans. The atlas covered 99% of the population using only three components. Also, the method outperformed the standard method in reconstruction. Encoding shapes as ensembles of elements in the \(\mathbb{SE}(3)\) group is a simple way of constructing compact shape models.
Chapter PDF
Similar content being viewed by others
References
Babalola, K.O., Patenaude, B., Aljabar, P., Schnabel, J.A., Kennedy, D., Crum, W.R., Smith, S., Cootes, T.F., Jenkinson, M., Rueckert, D.: Comparison and evaluation of segmentation techniques for subcortical structures in brain MRI. In: Metaxas, D., Axel, L., Fichtinger, G., Székely, G. (eds.) MICCAI 2008, Part I. LNCS, vol. 5241, pp. 409–416. Springer, Heidelberg (2008)
Cootes, T.F., Taylor, C.J., Cooper, D.H., Graham, J.: Active shape models - their training and application. Comput. Vis. Image Underst. 61(1), 38–59 (1995)
Davatzikos, C., Tao, X., Shen, D.: Hierarchical active shape models, using the wavelet transform. IEEE Trans. Med. Imaging (USA) 22(3), 414–423 (2003)
Davies, R.H., Twining, C.J., Cootes, T.F., Waterton, J.C., Taylor, C.J.: A minimum description length approach to statistical shape modeling. IEEE Trans. Med. Imaging 21(5), 525–537 (2002)
Feng, J., Ip, H.H.S.: A muti-resolution statistical deformable model (MISTO) for soft-tissue organ reconstruction. Pattern Recognit. 42(7), 1543–1558 (2009)
Fletcher, P.T., Lu, C., Pizer, S.M., Joshi, S.: Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Trans. Med. Imaging 23(8), 995–1005 (2004)
Foruzan, A.H., Chen, Y.W., Hori, M., Sato, Y., Tomiyama, N.: Capturing large shape variations of liver using population-based statistical shape models. Int. J. Comp. Assist. Radiol. Surg. 9, 967–977 (2014)
Heap, T., Hogg, D.: Extending the point distribution model using polar coordinates. In: Hlaváč, V., Šára, R. (eds.) CAIP 1995. LNCS, vol. 970, pp. 130–137. Springer, Heidelberg (1995)
Hefny, M.S.: Analysis of Discrete Shapes Using Lie Groups. Ph.D. thesis, Queen’s University (2014)
Hefny, M.S., Pichora, D.R., Rudan, J.F., Ellis, R.E.: Manifold statistical shape analysis of the distal radius. Int. J. Comp. Assist. Radiol. Surg. 9(supp. 1), S35–S42 (2014)
Hefny, M.S., Rudan, J.F., Ellis, R.E.: A matrix lie group approach to statistical shape analysis of bones. Stud. Health Technol. Inform. 196, 163–169 (2014)
Hotelling, H.: Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 24, 417–441 (1933)
Lamecker, H., Lange, T., Seebass, M.: A statistical shape model for the liver. In: Dohi, T., Kikinis, R. (eds.) MICCAI 2002, Part II. LNCS, vol. 2489, pp. 421–427. Springer, Heidelberg (2002)
Okada, T., Linguraru, M.G., Yoshida, Y., Hori, M., Summers, R.M., Chen, Y.-W., Tomiyama, N., Sato, Y.: Abdominal multi-organ segmentation of CT images based on hierarchical spatial modeling of organ interrelations. In: Yoshida, H., Sakas, G., Linguraru, M.G. (eds.) Abdominal Imaging. LNCS, vol. 7029, pp. 173–180. Springer, Heidelberg (2012)
Pennec, X.: Intrinsic statistics on Riemannian nanifolds: basic tools for geometric measurements. J. Math. Imag. Vis. 25, 127–154 (2006)
Sommer, S., Lauze, F., Hauberg, S., Nielsen, M.: Manifold valued statistics, exact principal geodesic analysis and the effect of linear approximations. In: Daniilidis, K., Maragos, P., Paragios, N. (eds.) ECCV 2010, Part VI. LNCS, vol. 6316, pp. 43–56. Springer, Heidelberg (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Hefny, M.S., Okada, T., Hori, M., Sato, Y., Ellis, R.E. (2015). A Liver Atlas Using the Special Euclidean Group. In: Navab, N., Hornegger, J., Wells, W., Frangi, A. (eds) Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2015. MICCAI 2015. Lecture Notes in Computer Science(), vol 9350. Springer, Cham. https://doi.org/10.1007/978-3-319-24571-3_29
Download citation
DOI: https://doi.org/10.1007/978-3-319-24571-3_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-24570-6
Online ISBN: 978-3-319-24571-3
eBook Packages: Computer ScienceComputer Science (R0)