Abstract
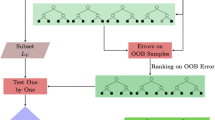
Machine learning methods can be used for estimating the class membership probability of an observation. We propose an ensemble of optimal trees in terms of their predictive performance. This ensemble is formed by selecting the best trees from a large initial set of trees grown by random forest. A proportion of trees is selected on the basis of their individual predictive performance on out-of-bag observations. The selected trees are further assessed for their collective performance on an independent training data set. This is done by adding the trees one by one starting from the highest predictive tree. A tree is selected for the final ensemble if it increases the predictive performance of the previously combined trees. The proposed method is compared with probability estimation tree, random forest and node harvest on a number of bench mark problems using Brier score as a performance measure. In addition to reducing the number of trees in the ensemble, our method gives better results in most of the cases. The results are supported by a simulation study.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Ali, K. M., & Pazzani, M. J. (1996). Error reduction through learning multiple descriptions. Machine Learning, 24, 173–202.
Breiman, L. (2001). Random forests. Machine Learning, 45, 5–32.
Gneiting, T., & Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association, 102, 359–378.
Gul, A., Khan, Z., Mahmoud, O., Perperoglou, A., Miftahuddin, M., Adler, W., et al. (2015). Ensemble of k-nearest neighbour classifiers for class membership probability estimation. In The Proceedings of European Conference on Data Analysis, 2014.
Hothorn, T., & Lausen, B. (2003). Double-bagging: Combining classifiers by bootstrap aggregation. Pattern Recognition, 36, 1303–1309.
Kruppa, J., Liu, Y., Biau, G., Kohler, M., Konig, I. R., Malley, J. D., et al. (2014a). Probability estimation with machine learning methods for dichotomous and multicategory outcome: Theory. Biometrical Journal, 56, 534–563.
Kruppa, J., Liu, Y., Diener, H. C., Weimar, C., Konig, I. R., & Ziegler, A. (2014b). Probability estimation with machine learning methods for dichotomous and multicategory outcome: Applications. Biometrical Journal, 56, 564–583.
Kruppa, J., Ziegler, A., & Konig, I. R. (2012). Risk estimation and risk prediction using machine-learning methods. Human Genetics, 131, 1639–1654.
Liaw, A., & Wiener, M. (2002). Classification and regression by random forest. R News, 2, 18–22.
Maclin, R., & Opitz, D. (2011). Popular ensemble methods: An empirical study. Journal of Artificial Research, 11, 169–189.
Mahmoud, O., Harrison, A., Perperoglou, A., Gul, A., Khan, Z., & Lausen, B. (2014b). propOverlap: Feature (Gene) selection based on the proportional overlapping scores. R package version 1.0. http://CRAN.R-project.org/package=propOverlap
Mahmoud, O., Harrison, A., Perperoglou, A., Gul, A., Khan, Z., Metodiev, M. V., et al. (2014a). A feature selection method for classification within functional genomics experiments based on the proportional overlapping score. BMC Bioinformatics, 15, 274.
Malley, J., Kruppa, J., Dasgupta, A., Malley, K., & Ziegler, A. (2012). Probability machines: Consistent probability estimation using nonparametric learning machines. Methods of Information in Medicine, 51, 74–81.
Meinshausen, N. (2010). Node harvest. The Annals of Applied Statistics, 4, 2049–2072.
Platt, J. C. (2000). Probabilistic outputs for support vector machines and comparison to regularized likelihood methods. In A. J. Smola, P. Bartlett, B. Schölkopf, & D. Schuurmans (Eds.), Advances in large margin classifiers (pp. 61–74). Cambridge, MA: MIT Press.
R Core Team. (2014). R: A language and environment for statistical computing. http://www.R-project.org/
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Khan, Z. et al. (2016). An Ensemble of Optimal Trees for Class Membership Probability Estimation. In: Wilhelm, A., Kestler, H. (eds) Analysis of Large and Complex Data. Studies in Classification, Data Analysis, and Knowledge Organization. Springer, Cham. https://doi.org/10.1007/978-3-319-25226-1_34
Download citation
DOI: https://doi.org/10.1007/978-3-319-25226-1_34
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-25224-7
Online ISBN: 978-3-319-25226-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)