Skip to main content
Springer Nature Link
Log in

Fuzzy Connectedness Segmentation: A Brief Presentation of the Literature

  • Conference paper
  • First Online:
Combinatorial Image Analysis (IWCIA 2015)

Part of the book series: Lecture Notes in Computer Science ((LNIP,volume 9448))

Included in the following conference series:

  • 1188 Accesses

Abstract

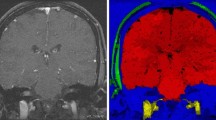
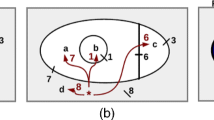
For any positive integer M, M-object fuzzy connectedness (FC) segmentation is a methodology for finding M objects in a digital image based on user-specified seed points and user-specified functions, called (fuzzy) affinities, which map each pair of image points to a value in the real interval [0, 1]. FC segmentation has been used with considerable success on biomedical and other images. We provide a brief presentation of the literature on the topic of FC segmentation.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Badura, P., Pietka, E.: Soft computing approach to 3D lung nodule segmentation in CT. Comput. Biol. Med. 53, 230–243 (2014)

    Article  Google Scholar 

  2. Bejar, H.H.C., Miranda, P.A.V.: Oriented relative fuzzy connectedness: theory, algorithms, and applications in image segmentation. In: 27th SIBGRAPI Conference on Graphics, Patterns and Images, pp. 304–311. IEEE Computer Society, Washington, DC (2014)

    Google Scholar 

  3. Carvalho, B.M., Garduño, E., Santos, I.O.: Skew divergence-based fuzzy segmentation of rock samples. J. Phys. Conf. Ser. 490, 012010 (2014)

    Article  Google Scholar 

  4. Carvalho, B.M., Gau, C.J., Herman, G.T., Kong, T.Y.: Algorithms for fuzzy segmentation. Pattern Anal. Appl. 2, 73–81 (1999)

    Article  Google Scholar 

  5. Carvalho, B.M., Herman, G.T., Kong, T.Y.: Simultaneous fuzzy segmentation of multiple objects. Electron. Notes Discrete Math. 12, 3–22 (2003)

    Article  MathSciNet  Google Scholar 

  6. Carvalho, B.M., Herman, G.T., Kong, T.Y.: Simultaneous fuzzy segmentation of multiple objects. Discrete Appl. Math. 151, 55–77 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  7. Carvalho, B.M., Souza, T.S., Garduño, E.: Texture fuzzy segmentation using adaptive affinity functions. In: 27th ACM Symposium on Applied Computing, pp. 51–53. ACM, New York (2012)

    Google Scholar 

  8. Chen, L.: 3-D fuzzy digital topology and its application. Geophys. Prospect. Petrol. 24(2), 86–89 (1985). [In Chinese]

    Google Scholar 

  9. Chen, L.: The \(\lambda \)-connected segmentation algorithm and the optimal algorithm for split-and-merge segmentation. Chin. J. Comput. 14, 321–331 (1991). [In Chinese]

    Google Scholar 

  10. Chen, L., Berkey, F.T., Johnson, S.A.: Application of a fuzzy object search technique to geophysical data processing. In: SPIE 2180, Nonlinear Image Processing V, pp. 300–309. SPIE, Bellingham, WA (1994)

    Google Scholar 

  11. Chen, L., Cheng, H., Zhang, J.: Fuzzy subfiber and its application to seismic lithology classification. Inform. Sci. Appl. 1, 77–95 (1994)

    MATH  Google Scholar 

  12. Ciesielski, K.C., Herman, G.T., Kong, T.Y.: General theory of fuzzy connectedness segmentations. http://math.wvu.edu/~kcies/publications.html (Submitted)

  13. Ciesielski, K.C., Miranda, P.A.V., Falcão, A.X., Udupa, J.K.: Joint graph cut and relative fuzzy connectedness image segmentation algorithm. Med. Image Anal. 17, 1046–1057 (2013)

    Article  Google Scholar 

  14. Ciesielski, K.C., Udupa, J.K.: Affinity functions in fuzzy connectedness based image segmentation I: equivalence of affinities. Comput. Vis. Image Und. 114, 146–154 (2010)

    Article  Google Scholar 

  15. Ciesielski, K.C., Udupa, J.K.: Affinity functions in fuzzy connectedness based image segmentation II: defining and recognizing truly novel affinities. Comput. Vis. Image Und. 114, 155–166 (2010)

    Article  Google Scholar 

  16. Ciesielski, K.C., Udupa, J.K.: Region-based segmentation: fuzzy connectedness, graph cut, and other related algorithms. In: Deserno, T.M. (ed.) Biomedical Image Processing, pp. 251–278. Springer, Berlin (2011)

    Google Scholar 

  17. Ciesielski, K.C., Udupa, J.K., Falcão, A.X., Miranda, P.A.V.: Fuzzy connectedness image segmentation in graph cut formulation: a linear-time algorithm and a comparative analysis. J. Math. Imaging Vis. 44, 375–398 (2012)

    Article  MATH  Google Scholar 

  18. Ciesielski, K.C., Udupa, J.K., Saha, P.K., Zhuge, Y.: Iterative relative fuzzy connectedness for multiple objects, allowing multiple seeds. Comput. Vis. Image Und. 107, 160–182 (2007)

    Article  Google Scholar 

  19. Deserno, T.M. (ed.): Biomedical Image Processing. Springer, Berlin (2011)

    MATH  Google Scholar 

  20. Dijkstra, E.W.: A note on two problems in connexion with graphs. Numer. Math. 1, 269–271 (1959)

    Article  MATH  MathSciNet  Google Scholar 

  21. Falcão, A.X., Stolfi, J., Lotufo, R.A.: The image foresting transform: theory, algorithms, and applications. IEEE Trans. Pattern Anal. 26, 19–29 (2004)

    Article  Google Scholar 

  22. Garduño, E., Herman, G.T.: Parallel fuzzy segmentation of multiple objects. Int. J. Imag. Syst. Tech. 18, 336–344 (2009)

    Article  Google Scholar 

  23. Garduño, E., Wong-Barnum, M., Volkmann, N., Ellisman, M.H.: Segmentation of electron tomographic data sets using fuzzy set theory principles. J. Struct. Biol. 162, 368–379 (2008)

    Article  Google Scholar 

  24. Gulyás, G., Dombi, J.: Computing equivalent affinity classes in a fuzzy connectedness framework. Acta Cybernetica 21, 609–628 (2014)

    MathSciNet  Google Scholar 

  25. Herman, G.T., Carvalho, B.M.: Multiseeded segmentation using fuzzy connectedness. IEEE Trans. Pattern Anal. 23, 460–474 (2001)

    Article  Google Scholar 

  26. Palágyi, K., Tschirren, J., Hoffman, E.A., Sonka, M.: Quantitative analysis of pulmonary airway tree structures. Comput. Biol. Med. 36, 974–996 (2006)

    Article  Google Scholar 

  27. Saha, P.K., Udupa, J.K.: Iterative relative fuzzy connectedness and object definition: theory, algorithms, and applications in image segmentation. In: IEEE Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA 2000), pp. 28–35. IEEE Computer Society, Washington, DC (2000)

    Google Scholar 

  28. Saha, P.K., Udupa, J.K.: Relative fuzzy connectedness among multiple objects: theory, algorithms, and applications in image segmentation. Comput. Vis. Image Und. 82, 42–56 (2001)

    Article  MATH  Google Scholar 

  29. Siebra, H., Carvalho, B.M., Garduño, E.: Fuzzy clustering of color textures using skew divergence and compact histograms: segmenting thin rock sections. J. Phys. Conf. Ser. 574, 012116 (2015)

    Article  Google Scholar 

  30. Tschirren, J., Hoffman, E.A., Mclennan, G., Sonka, M.: Intrathoracic airway trees: segmentation and airway morphology analysis from low-dose CT scans. IEEE Trans. Med. Imaging 24, 1529–1539 (2005)

    Article  Google Scholar 

  31. Udupa, J.K., Saha, P.K., Lotufo, R.A.: Relative fuzzy connectedness and object definition: theory, algorithms, and applications in image segmentation. IEEE Trans. Pattern Anal. 24, 1485–1500 (2002)

    Article  Google Scholar 

  32. Udupa, J.K., Samarasekera, S.: Fuzzy connectedness and object definition: theory, algorithms, and applications in image segmentation. Graph. Model. Im. Proc. 58, 246–261 (1996)

    Article  Google Scholar 

  33. Zhuge, Y., Udupa, J.K., Saha, P.K.: Vectorial scale-based fuzzy connected image segmentation. Comput. Vis. Image Und. 101, 177–193 (2006)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Science PhD Program, The Graduate Center, City University of New York, 365 Fifth Avenue, New York, NY, 10016, USA

    Gabor T. Herman & T. Yung Kong

  2. Computer Science Department, Queens College, City University of New York, 65-30 Kissena Boulevard, Flushing, NY, 11367, USA

    T. Yung Kong

  3. Department of Mathematics, West Virginia University, Morgantown, WV, 26506, USA

    Krzysztof Chris Ciesielski

Authors
  1. Gabor T. Herman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Yung Kong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Krzysztof Chris Ciesielski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gabor T. Herman .

Editor information

Editors and Affiliations

  1. SUNY Fredonia, Fredonia, New York, USA

    Reneta P. Barneva

  2. Advanced Computing and Microelectronics, Indian Statistical Institute, Kolkata, Germany

    Bhargab B. Bhattacharya

  3. SUNY Buffalo State, Buffalo, New York, USA

    Valentin E. Brimkov

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer International Publishing Switzerland

About this paper

Cite this paper

Herman, G.T., Kong, T.Y., Ciesielski, K.C. (2015). Fuzzy Connectedness Segmentation: A Brief Presentation of the Literature. In: Barneva, R., Bhattacharya, B., Brimkov, V. (eds) Combinatorial Image Analysis. IWCIA 2015. Lecture Notes in Computer Science(), vol 9448. Springer, Cham. https://doi.org/10.1007/978-3-319-26145-4_2

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-26145-4_2

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-26144-7

  • Online ISBN: 978-3-319-26145-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics