A New Approach to Model-Free Tracking with 2D Lidar

Abstract

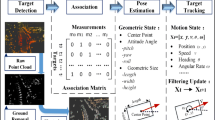
This paper presents a unified and model-free framework for the detection and tracking of dynamic objects with 2D laser range finders in an autonomous driving scenario. A novel state formulation is proposed that captures joint estimates of the sensor pose, a local static background and dynamic states of moving objects. In addition, we contribute a new hierarchical data association algorithm to associate raw laser measurements to observable states, and within which, a new variant of the Joint Compatibility Branch and Bound (JCBB) algorithm is introduced for problems with large numbers of measurements. The system is calibrated systematically on 7.5K labeled object examples and evaluated on 6K test cases, and is shown to greatly outperform an existing industry standard targeted at the same problem domain.

Appendix

In this appendix, we state the exact forms of the observation models applied to boundary points on the static background and dynamic objects respectively. All variables involved in what follows are defined in Sect. 4.1, and the function $\mathbf {u}$ maps a pair of 2D cartesian coordinates into polar coordinates.

Each boundary point j on the static background may potentially generate a laser measurement $\mathbf {z} = [r,\theta ]^T$, and hence its measurement model is the boundary point’s location in polar coordinates in the sensor’s frame of reference:

$$\begin{aligned} \mathbf {h}_j(\mathbf {x}) = \mathbf {u}(\mathbf {g}(\mathbf {x}_S,\mathbf {b}_j))\text{, } \;\mathbf {g}(\mathbf {x}_S,\mathbf {b}_j) = \mathbf {R}^T(\psi )\left( \left[ \begin{array}{c}x_j\\ y_j\end{array}\right] -\left[ \begin{array}{c}\alpha \\ \beta \end{array}\right] \right) \text{. } \end{aligned}$$

(9)

Each boundary point j on any dynamic track i may also give rise to a laser measurement, and the measurement model in this case is the 2D polar coordinates of the boundary point in the sensor frame, and is given by:

$$\begin{aligned} \mathbf {h}_j(\mathbf {x}) = \mathbf {u}(\mathbf {g}(\mathbf {x}_S,\mathbf {x}_T^i,\mathbf {p}_j^i))\text{, } \;\mathbf {g}(\mathbf {x}_S,\mathbf {x}_T^i,\mathbf {p}_j^i) = \mathbf {R}^T(\psi )\left( \mathbf {R}(\phi _i)\left[ \begin{array}{c}x_j^i\\ y_j^i\end{array}\right] +\left[ \begin{array}{c}\gamma _i\\ \delta _i\end{array}\right] -\left[ \begin{array}{c}\alpha \\ \beta \end{array}\right] \right) \text{. } \end{aligned}$$

(10)