Abstract
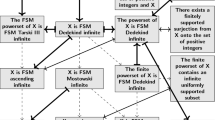
This paper presents the main steps in defining a Finitely Supported Mathematics by using sets with atoms. Such a mathematics generalizes the classical Zermelo-Fraenkel mathematics, and represents an appropriate framework to work with (infinite) structures in terms of finitely supported objects. We focus on the techniques of translating the Zermelo-Fraenkel results into this Finitely Supported Mathematics over infinite (possibly non-countable) sets with atoms. Two general methods of proving the finite support property for certain algebraic structures are presented. Finally, we provide a survey on the applications of the Finitely Supported Mathematics in experimental sciences.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
A multiset on an alphabet \(\varSigma \) is a function from \(\varSigma \) to \(\mathbb {N}\) where each element in \(\varSigma \) has associated its multiplicity.
- 2.
Let P be a predicate on A. We say that
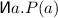 if P(a) is true for all but finitely many elements of A.
if P(a) is true for all but finitely many elements of A.
References
Alexandru, A., Ciobanu, G.: Nominal event structures. Rom. J. Inf. Sci. Technol. 15, 79–90 (2012)
Alexandru, A., Ciobanu, G.: Nominal techniques for \(\pi I\)-calculus. Rom. J. Inf. Sci. Technol. 16, 261–286 (2013)
Alexandru, A., Ciobanu, G.: Nominal groups and their homomorphism theorems. Fundamenta Informaticae 131(3–4), 279–298 (2014)
Alexandru, A., Ciobanu, G.: On the development of the Fraenkel-Mostowski set theory. Bull. Polytech. Inst. Jassy LX, 77–91 (2014)
Alexandru, A., Ciobanu, G.: A nominal approach for fusion calculus. Rom. J. Inf. Sci. Technol. 17(3), 265–288 (2014)
Alexandru, A., Ciobanu, G.: Mathematics of multisets in the Fraenkel-Mostowski framework. Bulletin Mathematique de la Societe des Sciences Mathematiques de Roumanie 58/106(1), 3–18 (2015)
Alexandru, A., Ciobanu, G.: Defining finitely supported mathematics over sets with atoms. In: Batsakis, S., Bobalo, Y., Ermolayev, V., Kharchenko, V., Kobets, V., Kravtsov, H., Mayr, H.C., Nikitchenko, M., Peschanenko, V., Spivakovsky, A., Yakovyna, V., Zholtkevych, G. (eds.) 4th International Workshop on Algebraic, Logical, and Algorithmic Methods of System Modeling, Specification and Verification, vol. 1356, pp. 382–395 (2015). http://CEUR-WS.org
Alexandru, A., Ciobanu, G.: Generalized multisets: from ZF to FSM. Comput. Inform. 34(5), 1133–1150 (2015)
Alexandru, A., Ciobanu, G.: Static analysis in finitely supported mathematics. In: 17th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing. IEEE Computer Society Press (2015, in press)
Alexandru, A., Ciobanu, G.: Pawlak approximations in the framework of nominal sets. J. Multiple-Valued Logic Soft Comput. 26(3) (2016, in press)
Alexandru, A., Ciobanu, G.: Finitely supported subgroups of a nominal group. Mathematical Reports 18(2) (2016)
Banach, S., Tarski, A.: Sur la décomposition des ensembles de points en parties respectivement congruentes. Fundamenta Mathematicae 6, 244–277 (1924)
Barwise, J.: Admissible Sets and Structures: An Approach to Definability Theory. Perspectives in Mathematical Logic, vol. 7. Springer, Berlin (1975)
Bojańczyk, M., Lasota, S.: Fraenkel-Mostowski sets with non-homogeneous atoms. In: Finkel, A., Leroux, J., Potapov, I. (eds.) RP 2012. LNCS, vol. 7550, pp. 1–5. Springer, Heidelberg (2012)
Bojanczyk, M.: Nominal monoids. Theor. Comput. Syst. 53, 194–222 (2013)
Bojanczyk, M., Braud, L., Klin, B., Lasota, S.: Towards nominal computation. In: 39th ACM Symposium on Principles of Programming Languages, pp. 401–412 (2012)
Bojanczyk, M., Klin, B., Lasota, S.: Automata with group actions. In: 26th Symposium on Logic in Computer Science, pp. 355–364. IEEE Computer Society Press (2011)
Bojanczyk, M., Klin, B., Lasota, S., Torunczyk, S.: Turing machines with atoms. In: 28th Symposium on Logic in Computer Science, pp. 183–192. IEEE Computer Society Press (2013)
Bojanczyk, M., Lasota, S.: A machine-independent characterization of timed languages. In: 39th International Colloquium on Automata, Languages and Programming, pp. 92–103 (2012)
Bojanczyk, M., Torunczyk, S.: Imperative programming in sets with atoms. In: D’Souza, D., Kavitha, T., Radhakrishnan, J. (eds.) IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, vol. 18, pp. 4–15. LIPIcs (2012)
Cohen, P.J.: The Independence of the Axiom of Choice. Stanford University, Mimeographed (1963)
Fraenkel, A.: Zu den grundlagen der Cantor-Zermeloschen mengenlehre. Mathematische Annalen 86, 230–237 (1922)
Gabbay, M.J.: The pi-calculus in FM. In: Kamareddine, F.D. (ed.) Thirty Five Years of Automating Mathematics. Applied Logic Series, vol. 28, pp. 247–269. Springer, The Netherlands (2003)
Gabbay, M.J., Pitts, A.M.: A new approach to abstract syntax with variable binding. Formal Aspects Comput. 13, 341–363 (2001)
Gandy, R.: Church’s thesis and principles for mechanisms. In: Barwise, J., Keisler, H.J., Kunen, K. (eds.) The Kleene Symposium, pp. 123–148. North-Holland, Amsterdam (1980)
Gödel, K.: The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis with the Axioms of Set Theory. Annals of Mathematics Studies. Princeton University Press, Princeton (1940)
Herrlich, H.: Axiom of Choice. Lecture Notes in Mathematics. Springer, Heidelberg (2006)
Howard, P., Rubin, J.E.: Consequences of the Axiom of Choice. Mathematical Surveys and Monographs, vol. 59. American Mathematical Society, Providence (1998)
Jech, T.J.: The Axiom of Choice. Studies in Logic and the Foundations of Mathematics. North-Holland, Amsterdam (1973)
Krohn, K., Rhodes, J.: Algebraic theory of machines: prime decomposition theorem for finite semigroups and machines. Trans. Am. Math. Soc. 116, 450–464 (1965)
Lindenbaum, A., Mostowski, A.: Uber die unabhangigkeit des auswahlsaxioms und einiger seiner folgerungen. Comptes Rendus des Seances de la Societe des Sciences et des Lettres de Varsovie. 31, 27–32 (1938)
Parrow, J., Victor, B.: The update calculus. In: Johnson, M. (ed.) Algebraic Methodology and Software Technology. LNCS, vol. 1349, pp. 409–423. Springer, Heidelberg (1997)
Petrisan, D.: Investigations into algebra and topology over nominal sets. Ph.D. thesis, University of Leicester (2011)
Pitts, A.M.: Alpha-structural recursion and induction. J. ACM 53, 459–506 (2006)
Pitts, A.M.: Nominal Sets Names and Symmetry in Computer Science. Cambridge University Press, Cambridge (2013)
Sangiorgi, D.: \(\pi \)-calculus, internal mobility, and agent-passing calculi. Rapport INRIA no.2539 (1995)
Shinwell, M.R.: The fresh approach: functional programming with names and binders. Ph.D. thesis, University of Cambridge (2005)
Tarski, A.: What are logical notions? Hist. Philos. Logic 7, 143–154 (1986)
Turner, D.: Nominal Domain Theory for Concurrency. Technical report no.751, University of Cambridge (2009)
Urban, C.: Nominal techniques in Isabelle/HOL. J. Autom. Reasoning 40, 327–356 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Alexandru, A., Ciobanu, G. (2016). Main Steps in Defining Finitely Supported Mathematics. In: Yakovyna, V., Mayr, H., Nikitchenko, M., Zholtkevych, G., Spivakovsky, A., Batsakis, S. (eds) Information and Communication Technologies in Education, Research, and Industrial Applications. ICTERI 2015. Communications in Computer and Information Science, vol 594. Springer, Cham. https://doi.org/10.1007/978-3-319-30246-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-30246-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-30245-4
Online ISBN: 978-3-319-30246-1
eBook Packages: Computer ScienceComputer Science (R0)


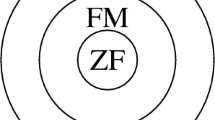

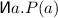 if P(a) is true for all but finitely many elements of A.
if P(a) is true for all but finitely many elements of A.