Automatic Pose Estimation Using Contour Information from X-Ray Images

Abstract

An automatic approach to model-based pose estimation is presented that only uses given, segmented contours in X-ray images. The pose estimation based on Fourier Descriptors is extended to an arbitrary, calibrated stereo setup and eliminates the need for a manually given initialization. To further refine the pose, local and global optimization schemes that minimize the distance between the segmentation and the projected object over the six pose parameters are compared. Experiments show that a sampling-based optimization outperforms gradient-based methods and the sampling can be further improved to fit the given imaging setup and the object of interest. Simulated data shows that the pose can be estimated nearly perfect in stereo setups and yields highly accurate results on single-view setups. Clinical data supports these findings.

1 Introduction

Inferring three-dimensional information from two-dimensional images is an important part of bio-medical image analysis. Three-dimensional data is rarely acquired in clinical routine due to higher costs, the additional time to gather and process the data or simply because the imaging device is not available. Nevertheless, this particular information is often needed in image guided surgery and preoperative planning [3] or the evaluation of three-dimensional movements like implant migration [4] and knee kinematics [5].

Pose estimation is one part of the challenging task of relating two-dimensional and three-dimensional data. Given a model of the object of interest and at least one projection, the goal is to determine the pose of the model that best explains the projections. Using rigid objects the pose consists of six parameters: the location (three translations) and orientation (three rotations) of a known object. In a bio-medical context bones or endoprostheses are usually of interest.

Many algorithms have been developed to assess the problem of pose estimation in a clinical context [6]. Typically, these methods require a manual initialization to start a minimization process that aligns the segmented and the projected contours [4, 7]. Depending on the amount of data that has to be processed, this can be a time-consuming task, limiting the usability in clinical routine. Additionally, stereo setups with orthogonal cameras are often used to ideally represent the three-dimensional space. In a clinical environment this may be impracticable. Monocular setups or smaller angles between the cameras have to be considered.

Automatic or semi-automatic pose estimation are commonly proposed for fluoroscopic images [8]. Temporal relations are used to initialize the following frame. However, a manually provided pose is still required to start the process at the first frame or to guide it during certain key frames.

Another often neglected problem are projective characteristics of objects of interest in a clinical context. Human long bones and many endoprostheses may show little rotational variation about one axis and radiopaque objects like metal implants can only be processed by their contour, further limiting usable features.

In our work we provide a fully automatic method for the pose estimation of rigid objects from X-ray images in a monocular or stereo imaging setup. Given the segmented contour of the object in the images an initial pose is computed using Fourier Descriptors and a matching to a database of simulated projections. The pose is further refined by minimizing the distance between the given segmentation and the projection of the model over the pose parameters. We combine local and global optimization schemes, such that properties of the imaging setup and the object of interest are considered.

2 Methods

2.1 Fourier Descriptor

The Fourier Descriptor (FD) offers a representation of a two-dimensional shape that is invariant to translation, scale and rotation if properly normalized. It allows to easily compare similar objects and is mostly used for shape discrimination and retrieval [9]. The FD uses the discrete Fourier transform to convert a two-dimensional closed contour into the one-dimensional frequency domain (Fig. 1).

Fig. 1.

X-ray image of a total hip implant (a), sampled contour (b) and its normalize Fourier Descriptor (c). Displayed are magnitude $|S_n|$ and phase angle $\arg (S_n)$ of the FD computed with 128 equidistant points.

The boundary of the object is sampled by $N = 2^m$ equidistant points $(x_n,y_n)$ given in the complex plane:

$$\begin{aligned} c_n = x_n + jy_n, \, n=0,\ldots ,N-1 \, . \end{aligned}$$

(1)

The Fourier transform of this closed contour is given by

$$\begin{aligned} C_k = \sum _{n=0}^{N-1} c_n\exp \left( -j\frac{2\pi kn}{N}\right) , \, k=0,\ldots ,N-1 \, . \end{aligned}$$

(2)

Properties of the transform are exploited to normalize the coefficients $C_k$. Translations of the contour in the image plane only have an effect on the coefficient $C_0$. Setting

$$\begin{aligned} \hat{C}_0 = 0 \end{aligned}$$

(3)

centers the contour and normalizes for translational differences. The size of the object affects the magnitude of the coefficients $C_k$. Ensuring that $|C_1| = 1$ holds, normalizes for the scale of the shape. Rotational differences and the respective starting point of the contour affect the phase of the coefficients $C_k$. Thus, the normalized FD are given by

$$\begin{aligned} \hat{C}_k = \frac{C_k}{|C_1|}\exp \left( j\frac{\arg (C_1)+\arg (C_{N-1})}{2}\right) \exp \left( jk\frac{\arg (C_1)-\arg (C_{N-1})}{2}\right) \,, \end{aligned}$$

(4)

where $\arg (z)$ denotes the phase of the complex number z. Rotations are normalized by the main ellipse of the shape, the starting point is shifted to ensure that $\arg (\hat{C}_1) = \arg (\hat{C}_{N-1}) = 0$ always holds. However, a rotation of the ellipse about $\pm \pi$ remains indeterminable and thus, a second normalization

$$\begin{aligned} \hat{C}_k^\pi = \hat{C}_k \exp \left( j\pi (k-1)\right) \end{aligned}$$

(5)

has to be considered.

2.2 Pose Estimation with Fourier Descriptors

The properties of the Fourier Descriptor enable a relatively fast and intuitive approach to estimate the pose without the need for a manual initialization. We follow the work of Banks et al. [1] and extend it to an arbitrary, calibrated imaging setup.

By using the normalized FD to describe a projection of an object, the six-dimensional pose space can be reduced to two rotational parameters. Translations in the three-dimensional space are covered by the invariance of the descriptor to scale and translation in the image plane. The rotational invariance limits the distinguishable three-dimensional rotations. By sampling over the remaining two rotations the whole pose space can be covered. In the following we briefly explain our pose estimation procedure.

A database of views of the object over two rotations is built. Visually speaking, we obtain all possible FD of the projected object by viewing the object from positions lying on a sphere with the object located at the center. Missing parameters of the pose are inferred by the normalization factors, the known pose in the database and the geometric properties of the imaging setup after finding the best matching view in the database.

The database is built by simulating the imaging process with a known three-dimensional model of the object of interest. With a simulated camera at the z-axis the object centered on the same axis is first rotated around the x-axis by an angle $\omega _x \in \left[ -\pi /2, \pi /2\right]$, followed by a rotation around the y-axis by an angle $\omega _y \in \left[ -\pi , \pi \right]$ (see Fig. 2). To each pair of angles $(\omega _x, \omega _y)$ the normalized FD $\hat{C}(\omega _x, \omega _y)$ and the normalization factors are stored.

Fig. 2.

Simulation setup to build the database of model views.

The pose estimation is carried out using a single view of the object in a calibrated setup, e.g. we know the projection matrix P that projects three-dimensional points into the image plane. In particular, the focal length f (distance from the x-ray tube to the X-ray cassette), the camera center (location of the focus of the x-ray tube), the pixel size $(s_x,s_y)$ of the detector and the principal point $(p_x, p_y)$ are needed. Intrinsic camera parameters of the simulated and the real imaging setup do not need to coincide, but should be roughly comparable.

After segmenting the object of interest in the image the normalized Fourier Descriptors $\hat{C}^{input}$ and $\hat{C}^{\pi , input}$ are computed. For the sake of simplicity, we only refer to $\hat{C}^{input}$. However, it should be noted that both possible normalizations have to be considered. In order to find the most similar FD of our database to $\hat{C}^{input}$, we search for the closes FD in terms of the Euclidian distance:

$$\begin{aligned} \hat{C}^{db} = \mathop {\text {arg}\,\text {min}}\limits _{(\omega _x,\omega _y)}\sum _{i=2}^{N-1}\left\| \hat{C}_i(\omega _x,\omega _y)-\hat{C}_i^{input}\right\| _2 \, . \end{aligned}$$

(6)

The in-plane rotation, i.e. the rotation about the z-axis, is estimated by

$$\begin{aligned} \omega _z = \frac{\arg (C_1^{input}) + \arg (C_{N-1}^{input})}{2} - \frac{\arg (C_1^{db}) + \arg (C_{N-1}^{db})}{2} \, , \end{aligned}$$

(7)

the difference in the rotations used for normalization. The angle has to be adjusted by $\pi$ if the second normalization $\hat{C}^\pi$ was used for the input contour. With the intercept theorem the distance of the object from the camera center, i.e. the translation in direction of the z-axis, is given by

$$\begin{aligned} t_z = \left( \frac{|C^{db}_1|}{|C^{input}_1|}\frac{f^{input}}{f^{db}}-1\right) d_z^{db} \, . \end{aligned}$$

(8)

The formula uses the scale factor as magnification factor in the projection and the distance $d_z^{db}$ of the object to the camera center in the database setup. Figure 3 shows the geometric explanation of (8).

Fig. 3.

Geometric explanation of depth estimation using FD. Simulated and real camera are aligned and the depth is related to the apparent size of the object in the image planes.

The remaining parameters are estimated in a similar fashion using the in-plane rotation and the different magnification factors. Translational parameters can be estimated by

$$\begin{aligned} \begin{pmatrix} t_x \\ t_y \end{pmatrix} = \frac{1}{N} \frac{d_z^{db}}{f^{db}}\left( \frac{|C^{db}_1|}{|C^{input}_1|} \begin{pmatrix} x^{input} \\ y^{input} \end{pmatrix} - R(\omega _z) \begin{pmatrix} x^{db} \\ y^{db} \end{pmatrix} \right) \, , \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{pmatrix} x^{input}) \\ y^{input} \end{pmatrix} = \begin{pmatrix} s_x^{input}\left( Re(C^{input}_0) - p_x^{input}\right) \\ s_y^{input}\left( Im(C^{input}_0)-p_y^{input}\right) \end{pmatrix} \end{aligned}$$

(10)

relates the perceived translation in the image plane to the scale of the camera coordinate system. The database entry is adjusted analogously. Lastly,

$$\begin{aligned} \begin{pmatrix} \omega _x \\ \omega _y \end{pmatrix} = \begin{pmatrix} \omega ^{db}_x \\ \omega ^{db}_y \end{pmatrix} - R(-\omega _z) \begin{pmatrix} \arctan \left( x^{input}/f^{input}\right) \\ \arctan \left( y^{input}/f^{input}\right) \end{pmatrix} \end{aligned}$$

(11)

uses the inclination to define the left rotational parameters. In a final step, the object has to be transformed to the world coordinate system by using the extrinsic parameters of the real camera setup.

2.3 Pose Estimation Using Contour Distance

The Fourier Descriptors allow for an approximate estimation of the object pose dependent on pose space coverage. A more exact pose can be derived by directly minimizing the distance between the segmented contour $c^{seg}$ in the image and the projection of the object $c^{proj}$. For each point on the segmented contour the closest point on the projected contour is identified and the sum the distances is minimized over the pose of the object:

$$\begin{aligned} E(\omega ,t) = d\left( c^{seg}, c^{proj}(\omega ,t)\right) = \frac{1}{n}\sum _{i=1}^n \min _j \left\| c^{seg}_i -c^{proj}_j(\omega ,t)\right\| ^2 \rightarrow \min !\, . \end{aligned}$$

(12)

In a stereo setup the energy for both views is simply added.

A standard procedure in pose estimation is the Iterative Closest Points (ICP) algorithm that estimates the optimal transformation between two point clouds. A variant directly relates the two-dimensional points of the contour to the three-dimensional model to infer the pose [11]. ICP solves the problem in (12) indirectly by minimizing the distance between the correspondences in each step.

In general, the ICP method is fast and fairly robust. However, the solution is a local minimum and depends on the starting point. Especially objects with low rotational variance suffer from an energy function with many broad, local minima. Unfortunately, those objects are common in the bio-medical context. Long bones or many implants fall in this category and often lack the desired accuracy in the estimated pose.

Other methods solve (12) by directly optimizing over the six pose parameters in an iterative manner. Given a starting pose $\left( \omega ^{(0)}, t^{(0)}\right) ^{\mathsf T}\in \mathbb {R}^6$ we search for a series of updates

$$\begin{aligned} \begin{pmatrix} \omega ^{(i+1)} \\ t^{(i+1)} \end{pmatrix} = \begin{pmatrix} \omega ^{(i)} \\ t^{(i)} \end{pmatrix} + \begin{pmatrix} \varDelta \omega \\ \varDelta t \end{pmatrix}, \, i\ge 0 \end{aligned}$$

(13)

that gradually minimizes the energy (12). Non-linear optimization schemes are either derivative-free like the Nelder-Mead method or use the (approximated) gradient to define a descending direction like Sequential Quadratic Programming [10]. Again, these methods guarantee only a local minimum.

Global optimization schemes like Simulated Annealing [2] often incorporate a stochastic component and the search direction is found randomly to further explore the function.

2.4 A Combined Approach

Finally, we aim to combine the approaches introduced above. Fourier Descriptors and a database matching are used to estimate an initial pose which is further refined by minimizing the contour distance. Firstly, we extend the descriptor-based pose estimation to a stereo setup. Afterwards, we briefly explain the additional refinement steps.

In the single-view setup the segmented contour is compared to each database entry and the best matching entry is used to estimate the pose as described in Sect. 2.2. For a stereo setup the known geometry of the imaging setup can be incorporated to solve for ambiguities in the database matching. The two contours are matched to pairs that are feasible, i.e. the views in the database differ in the same angle as the cameras. One pose is estimated for each view and the poses are combined to preserve reliable pose parameters.

Without loss of generality, we assume both cameras lie in the xz-plane with one camera centered on the x-axis and the second camera rotated by an angle $\alpha$ around the y-axis. For the first camera the x- and y-coordinates are related to in-plane pose parameters. Translations along these axes and a rotation around the z-axis induce high changes in the image and these parameters are typically estimated more accurate. The z-coordinate on the other hand corresponds to depth information and often lacks precision.

Given two different sets of points $X^1 = \left\{ (x^1_i,y^1_i,z^1_i)^{\mathsf T},\, i=1,\ldots ,n\right\}$ and $X^2 = \left\{ (x^2_i,y^2_i,z^2_i)^{\mathsf T},\, i=1,\ldots ,n\right\}$ that describe the model in the estimated pose for each camera, we compute a mixed model

$$\begin{aligned} X_m = \left\{ \begin{pmatrix} \frac{1}{1+|\cos \alpha |} (x_i^1 + |\cos \alpha | x_i^2) \\ \frac{1}{2} (y_i^1 + y_i^2) \\ \frac{1}{1+|\cos \alpha |} (|\cos \alpha | z_i^1 + z_i^2) \end{pmatrix} ,\, i=1,\ldots , n \right\} \, . \end{aligned}$$

(14)

For an angle of $\alpha =90^\circ$ between the cameras the depth information of each camera is mainly ignored. Smaller camera angles require the usage of more depth information.

The computed model is topologically not identical to the original model. Either the first or the second model has to be rigidly transformed to match the model $X_m$. This yields the initial pose in the stereo setup as shown in Fig. 4. The initial pose is estimated using mostly two-dimensional information. To account for possible errors we use this pose to start an ICP-based pose estimation, relating three-dimensional model points to the two-dimensional contours from all available cameras.

Fig. 4.

Pose estimation using fourier descriptors in a stereo setup. Examples are shown for an individual (a) and combined estimation (b), with estimated models and their projections in green or red and the ground truth in blue (Color figure online).

Finally, the contour distance is minimized directly over the six pose parameters. We use a sampling-based optimization scheme and incorporate a priori information about the object and the imaging setup to guide the minimization process. The initial pose estimation yields errors that are, in general, not equally distributed among the pose parameters. Out-of-plane parameters are prone to errors and reflection planes or axes of symmetry induce further difficulties. To improve the sampling we estimate the errors that are typically induced in the initial pose estimation step. Random poses are generated in the simulation setup and pose estimation is performed using Fourier Descriptors. The measured errors in rotation and translation indicate suitable search directions, i.e. mean and standard deviation for the sampling step in the Simulated Annealing. Since those errors mostly depend on the angle between the cameras and the shape characteristics of the model the trained sampling parameters transfer well to comparable real setups.

3 Experiments and Results

We test our method on both simulated and real clinical data with a comparable X-ray setup.

3.1 Simulated Data

The simulations are carried out to demonstrate the ability of our method to automatically estimate the pose of the femoral part of a hip implant and the distal part of the femur. The used surface model of the implant is a three-dimensional scan of a short-stem total hip replacement manufactured by Aesculap, Germany. The model of the femur was reconstructed from a computed tomography. Figure 5 shows that both objects offer a relatively low amount of rotational variance around one axis and the estimation of an accurate pose is typically challenging even if a user generated input is given to guide the process.

Fig. 5.

Models used for experiments on simulated data and selected projections. The depicted contours are generated by rotating each model by an angle $\alpha \in \{-30^\circ ,-10^\circ ,10^\circ ,30^\circ \}$ to visualize the low rotational variance.

Pose estimation of these models is an integral part of the Model-based Roentgen Stereophotogrammetric Analysis [4]. The simulated imaging setup resembles a real clinical setup in this context. We assume the projective model of a pinhole camera to approximate a radiography and generate contours. A focal length of $1200\,mm$, an average distance of the object to the camera center of $1000\,mm$ and an image resolution of $0.2\,mm$ per pixel are used as standard imaging setup. We generate 200 random poses of the implant and the femur for evaluation. Rotations are drawn from an uniform distribution without further limitations to fully explore the capabilities of the method, translations are limited to a maximum of $100\,mm$. Additionally, we added a 5 % noise to the parameters of the base imaging setup for each generated pose.

Initial pose estimation was carried out with Fourier Descriptors computed with a database generated in the standard imaging setup. In a refinement step the energy (12) is minimized with Sequential Quadratic Programming (SQP) as described in [4], a state of the art approach in model-based implant migration analysis. Furthermore, we show the results of the Nelder-Mead method (NM) and two sampling-based optimization schemes: Simulated Annealing with equally distributed search directions (SA) and empirically estimated distributions (SA$^{est}$) as explained above. Results are listed in Table 1 showing the rotational errors (angle of rotation about one axis) and translational errors (Euclidean distance between object center).

Table 1. Mean and standard deviation of rotational and translational errors using simulated data (200 random poses) of the hip implant and the distal femur using different pose estimation methods.

We sampled the views in the database at approximately $5^\circ$ which corresponds to the computed error using Fourier Descriptors. Translational errors in the initial pose estimation are highly dependent on the imaging setup and show that the FD lack precision in the depth estimation. Subsequent refinement steps are capable of eliminating most of the error in the pose in a stereo setup, so the FD typically generate a reasonable starting pose.

The SQP approach yields results that are in the scope of the accuracy reported in the literature for stereo setups even without a manually initialization of the pose. Derivative-free optimization schemes outperform the gradient-based SQP in our test. Sampling-based optimization is the method of choice if a highly accurate pose is needed. Simulated Annealing shows the best results with nearly perfectly estimated poses in a stereo setup and acceptable poses in a monocular setup. Limiting the search direction by estimating possible errors does not only further improves the accuracy, but the minimum is typically found faster as well. However, computation time remains a disadvantage of these methods.

3.2 Clinical Data

In a second step we evaluate our method on 40 clinically acquired images. The used X-ray stereo images are from a short-stem total hip replacement study. The X-ray tubes are placed with an angle of approximately $40^\circ$. Every image is calibrated with the help of a calibration box. In the evaluation we focus on the pose estimation of the femur implant.

A few difficulties have to be addressed: the implant varies in size and the neck of the implant is often occluded by the hip socket. We ignore the neck part of the implant model and build a separate database for each size to apply the pose estimation via Fourier Descriptors. The implant contour is segmented by simple thresholding and automatically adjusted accordingly by analyzing the curvature along the contour. A sample of a segmented contour is displayed in Fig. 6a.

Fig. 6.

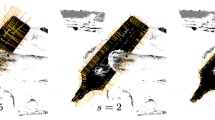
Effect of different energy minima on the computed pose. A sample image with the used segmented contour is shown in (a). Red rectangles show areas of interest, depicted in (b)–(d) with comparisons between segmented (blue) and projected (green) contours. The provided values show the energy (12) (Color figure online)

Unfortunately, no ground truth is known for the pose estimation of the implant in this study. We provide the found minimal energy (12) to compare different approaches and assume that errors in the pose and final energy are dependent as Fig. 6 suggests. However, the relation is highly non-linear. Even small improvements on the energy function may induce qualitatively better poses if out-of-plane parameters are optimized. The poses estimated by NM and SA$^{est}$ differ in about $2^\circ$ and $9^\circ$ compared to the SQP pose, but the energy of both poses is similar.

On average, we achieved a minimal energy of $3.16 \pm 0.94$ using SQP, $1.29 \pm 0.37$ using NM, $1.22 \pm 0.35$ using SA and $1.14 \pm 0.34$ using our proposed, adapted Simulated Annealing SA$^{est}$. Similar to the finding on the simulated data, the Nelder-Mead method and Simulated Annealing are superior to the SQP method typically used to solve this problem. On average, SA yields a minimal energy 10 % lower than NM. Although the improvement seems small, the mean of the pose differences are about $3^\circ$ in rotation and $0.8\,mm$ in translation. Main differences are rotations about the longitudinal axis and translations in out-of-plane direction. As Fig. 6 indicates the resulting poses of the SA typically show a qualitatively better agreement with the segmented contour.

4 Conclusion

We presented an automatic approach to model-based pose estimation in a clinical setup that utilizes X-ray images. No user-provided initial pose is needed. Given the contour of the object in one image the starting pose can be estimated by using Fourier Descriptors and a database of predefined, simulated views of the object.

The pose estimation process was extended to an arbitrary, calibrated imaging setup, so simulations to generate the database and the real setup do not have to share the same projective parameters. Monocular pose estimation is possible, however, if a second view of the object is provided the estimated poses can be combined using their known relation to greatly increase the quality of the estimation. In our simulated experiments sampling-based methods clearly outperformed the state of the art method used to assess implant migration. The space of probable search directions can be effectively limited by generating test samples and the optimization generally provides better results especially in a monocular test setup.

Experiments on clinical data further support the findings on simulated data. On general, the Simulated Annealing generates poses with lowest energy that agrees best with the segmented contour. The computational overhead justifies the higher accuracy.

The initial pose estimation presented in this paper requires that the object is fully visible in the image. Occlusions can only be handled by reducing the object to a common part displayed in all data as shown in the clinical experiments. Therefore, our proposed method is particularly suited for the pose estimation of radiopaque implants with clearly visible boundaries. Additional experiments are needed to further evaluate the applicability to pose estimation of bones, a more challenging task since the image contour is more prone to segmentation errors due to a lower contrast to its surrounding. Effects of these errors on the pose estimation process need to be investigated and incorporated accordingly.