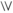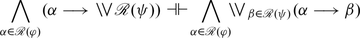Abstract
In the past few years, a tight connection has emerged between logics of dependency and logics of questions. The aim of this paper is to show that this connection stems from a fundamental relation existing between dependency and questions. Once we expand our view on logic by bringing questions into the picture, dependency emerges as a facet of the fundamental logical notion of entailment, namely entailment among questions. Besides providing an insightful conceptual picture, this perspective yields a general and well-behaved way of dealing with dependency in logical systems.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
A terminological remark is in order here: this technical usage of the word dependencyis not quite in line with the ordinary sense of the term, being weaker in one respect, and stronger in another. On the one hand, if νis already settled in a certain way in a context, independently of the answer to another question μ, then in our technical sense, ν doesdepend on μ, although in ordinary language, we would say that it does not. In this sense, the technical notion of dependency is weakerthan the ordinary notion, since dependencies are not required to be non-trivial. On the other hand, if in the given context the answer to νis partly determined by the answer to μ, and partly by other factors, then in our technical sense, νdoes notdepend on μ, although in the ordinary sense, it does: in our example, for instance, we would ordinarily say that the treatment depends on the symptoms, even though it is not fully determinedby the symptoms. In this sense, the technical notion of dependency is stronger than the usual notion. A better name for the relation that we are going to investigate would probably be determinacy; however, we will stick to the term dependencyfor the sake of consistency with the literature.
- 2.
The exact nature of possible worlds depends on the specific logical framework. Usually, a possible world may be identified with a model for the language at stake. In so-called intensionallogics, which aim at representing a whole variety of states of affairs in a single model, possible worlds are internalized as particular entities within the model. In some cases, several choices are possible, depending on one’s notion of a state of affairs. We will return to this issue in section 5.1.
- 3.
Information-oriented semantics are frequently considered in logic as a starting point for non-classical logics, such as intuitionistic logic or Veltman’s [37] data logic. However, non-classicality is in no way an inherent consequence of the information-oriented perspective: as we will see, it is utterly possible to give an information-based semantics for classical logic. Since our goal here is to show how classical logic can be extended naturally to questions, and notto reform classical logic, we will take such a semantics as our starting point.
- 4.
For the reader interested in the formal details, we will make this precise in Section 5.5.
- 5.
However, a complication for the variable approach should be noted here. In order for the translation from question-dependencies to variable-dependencies to work, we need the domain of our model to include more than individuals. For, depending on what our view on the notion of answer is, the unique answer to μat a world will either be a set of n-tuples for some n ≥ 0, as in categorial theories of questions [20, 29, 31], or it will be a set of worlds, as in the partition theory [13, 17]. Thus, we need to work with domains which include either arbitrary n-tuples of individuals or sets of worlds. While obviously possible, this seems to make the logical setup unnecessarily cumbersome.
- 6.
One may think of letting x μ denote at a world wthe set of all true answers to μat w. A moment’s reflection reveals that this will not work: saying that νis determined by μdoes not amount to saying that the set of answers to νis determined by the set of answers to μ, but merely to saying that any answer to μdetermines some answer to ν.
- 7.
We refer to ∨ as tensordisjunction to distinguish it from inquisitivedisjunction

, the question-forming that we will introduce below.
- 8.
In the dependence logic literature, the truth-conditionality property is referred to as flatness.
- 9.
It seems quite possible that, in natural language, an alternative question whether or βis only settled if we establish which one of αand βholds, to the exclusion of the other. If so, such a question should be translated in our translated in our formal language not as

, but as an exclusivedisjunction

. Nothing important in this paper hinges on this empirical issue. What matters is that, however construed, such questions—and therefore also dependencies between them—can be represented and reasoned about in the system.
- 10.
One may wonder what our formal notion of truth even means for questions, at an intuitive level. To answer this question, notice that, by persistence, we have w⊧μ ⇔ w ∈ sfor some s⊧μ. Thus, μis true at wjust in case there exists some information state that is true at wand which settles μ; in other words, just in case μhas a true answer at w. This converges with the proposal made by Belnap at the end of his paper Questions, answers, and presuppositions[2]: “I should like in conclusion to propose the following linguistic reform: that we all start calling a question ‘true’ just when some direct answer thereto is true.”
- 11.
This is not the terminology standardly used in inquisitive semantics. Usually (e.g., in [8]) sentences with a unique alternative are called assertions, and sentences with several alternatives are called inquisitive; due to a particular view of the effect of uttering a sentence, the term questionis reserved for formulas whose alternatives cover the whole set of possible worlds.
We prefer the term statementover assertion, since the latter is normally used to refer to a speech act, rather than to a sentence. As for the term question, we want to have a more liberal notion, since we also want to consider questions that can only be resolved in someworlds. This does not commit us to the view that questions are informativein the sense of [8], since we make no assumptions about the effect of uttering sentences in context. If we wanted to describe such an effect, we could do it along the lines of the system InqD π in [10].
- 12.
In particular, for n = 0 we have that the constancy atom = (p) of propositional dependence logic is equivalent to the polar question?p.
- 13.
One may be tempted to read μ → νas “νis determined by μ” and thus to think that μ → νshould qualify as a statement. That is not quite right, as witnessed by the fact that?p →?qis true at all worlds, and that its negation is a contradiction. If we wanted to have a formal counterpart of the statement “νis determined by μ,” we should proceed as follows. We should associate to every world wa “modal base,” that is, an information state σ(w). We would then introduce a binary operator Dwhich produces for any φand ψa statement with the following truth-conditions: w⊧D(φ, ψ) ⇔ σ(w)⊧φ → ψ. Since D(φ, ψ) is a statement, this determines the associated support conditions. In this way, we obtain a formula D(μ, ν) capable of being true or false at a world wdepending on whether νis determined by μat the associated information state σ(w).
- 14.
The idea of a “way for μto determine ν” will be made precise in the next section by means of the notion of resolutionsof a formula. We will see that the resolutions of an implication correspond to functions from resolutions of the antecedent to resolutions of the consequent. This is reminiscent of the Brouwer-Heyting-Kolmogorov interpretation of intuitionistic logic (see, e.g., [32]), where a proof of an implication is defined as a function that turns any proof of the antecedent into a corresponding proof of the consequent.
- 15.
The state | Γ | is the set of worlds where all formulas in Γare true, {w | w⊧αfor all α ∈ Γ}.
- 16.
In dependence logic, the analogue of the (⋅ )clis the operation of flattening, in which the dependence atoms occurring in a formula are replaced by ⊤. Like the classical variant operation, flattening always yields a classical formula whose support conditions with respect to singletons coincide with those of the original formula.
- 17.
- 18.
In order to simplify the proof, here we have replaced the conjunctive question?s 1∧?s 2(what are the symptoms?) by two distinct polar questions. This change is merely cosmetic, and dispensable.
- 19.
An anonymous reviewer pointed out that an equivalent semantic setup has been recently advocated by Väänänen [35] with a somewhat different motivation in mind. Väänänen’s goal is to develop a logic capable of expressing interesting properties of a set-theoretic multiverse, i.e., a structure containing a multitude of distinct models of set theory. In his system, formulas are evaluated with respect to a multiset of first-order models and to a function mapping each of these models to an assignment into the corresponding domain. While seemingly more complex, this setup is essentially equivalent to our setup based on sets of model-assignment pairs.
- 20.
Interestingly, the move we are making here has an almost exact parallel in the history of dynamic semantics. The fundamental idea of dynamic semantics is that the meaning of a sentence lies in its potential to bring about a change in an information state (either the conversational context or the hearer’s information state). Formally, what this means is that meanings are taken to be functions from information states to information states. In the Dynamic Predicate Logic (DPL) of [18], this approach was used to deal with anaphora, that is, with the process whereby pronouns get their referent. In this system, pronouns are modeled semantically as free variables. Accordingly, information states are taken to be sets of assignment, and a fixed underlying model is assumed. Later on, however, the dynamic approach was used by [38] to deal with modals and default reasoning; for these applications, it is crucial for an information state to contain different models, while assignments do not play a role. Finally, in [19], these lines of research were brought together in a unified framework, where states are taken to be sets of world-assignment pairs, just as in the present paper.
- 21.
This feature of \(\forall ^{d}\)has been exploited in linguistics by Brasoveanu and Farkas [3] to provide a solution to the long standing issue of how indefinites like a mantake their scope.
- 22.
These quantifiers have also been considered in the dependence logic literature, where they are denoted ∃1and \(\forall ^{1}\).
- 23.
For instance, it is easy to check that \(\forall ^{i}x\exists ^{i}y(x = y)\)is a valid formula, but \(\forall ^{d}x\exists ^{i}y(x = y)\)is not.
- 24.
- 25.
Notice in particular that, for n = 0, we have that the constancy atom = (x) of standard dependence logic is equivalent to the identity question λ x .
References
Abramsky, S., Väänänen, J.: From IF to BI. Synthese 167(2), 207–230 (2009)
Belnap, N.: Questions, answers, and presuppositions. J. Philos. 63(20), 609–611 (1966)
Brasoveanu, A., Farkas, D.F.: How indefinites choose their scope. Linguist. Philos. 34, 1–55 (2011)
Ciardelli, I.: Inquisitive semantics and intermediate logics. M.Sc. Thesis, University of Amsterdam (2009)
Ciardelli, I.: A first-order inquisitive semantics. In: Aloni, M., Bastiaanse, H., de Jager, T., Schulz, K. (eds.) Logic, Language, and Meaning: Selected Papers from the Seventeenth Amsterdam Colloquium, pp. 234–243. Springer, Berlin (2010)
Ciardelli, I.: Interrogative dependencies and the constructive content of inquisitive proofs. In: Kohlenbach, U., Barceló, P., de Queiroz, R. (eds.) Logic, Language, Information and Computation - 21st International Workshop. WoLLIC 2014. Lecture Notes in Computer Science, pp. 109–123. Springer, Berlin (2014)
Ciardelli, I., Roelofsen, F.: Inquisitive logic. J. Philos. Log. 40(1), 55–94 (2011)
Ciardelli, I., Groenendijk, J., Roelofsen, F.: Inquisitive semantics (2012). NASSLLI Lecture notes for a course at the North Americal School of Logic, Language, and Information. Unpublished, available at www.illc.uva.nl/inquisitivesemantics
Ciardelli, I., Groenendijk, J., Roelofsen, F.: Towards a logic of information exchange: an inquisitive witness semantics. In: Bezhanishvili, G., Marra, V., Löbner, S., Richter, F. (eds.) Logic, Language, and Computation: Revised Selected Papers from the Ninth International Tbilisi Symposium on Logic, Language, and Computation, pp. 51–72. Springer, Berlin (2013)
Ciardelli, I., Groenendijk, J., Roelofsen, F.: On the semantics and logic of declaratives and interrogatives. Synthese 192(6), 1689–1728 (2015)
Ebbing, J., Hella, L., Meier, A., Müller, J.S., Virtema, J., Vollmer, H.: Extended modal dependence logic. In: Libkin, L., Köhlenbach, U., de Queiroz, R. (eds.) Logic, Language, Information and Computation - 20th International Workshop. WoLLIC 2013. Lecture Notes in Computer Science, pp. 126–137. Springer, Berlin (2013)
Gamut, L.: Language, Logic and Meaning. Chicago University Press, Chicago, IL (1991)
Groenendijk, J.: The logic of interrogation. In: Matthews, T., Strolovitch, D. (eds.) Semantics and Linguistic Theory, pp. 109–126. Cornell University Press, Ithaca, NY (1999)
Groenendijk, J.: Inquisitive semantics: two possibilities for disjunction. In: Bosch, P., Gabelaia, D., Lang, J. (eds.) Seventh International Tbilisi Symposium on Language, Logic, and Computation. Springer, Berlin (2009)
Groenendijk, J.: Erotetic languages and the inquisitive hierarchy. In a Festschrift for Martin Stokhof (2011). http://dare.uva.nl/document/487828.
Groenendijk, J., Roelofsen, F.: Inquisitive semantics and pragmatics. Presented at the Workshop on Language, Communication, and Rational Agency at Stanford (2009). www.illc.uva.nl/inquisitivesemantics.
Groenendijk, J., Stokhof, M.: Studies on the semantics of questions and the pragmatics of answers. Ph.D. thesis, University of Amsterdam (1984)
Groenendijk, J., Stokhof, M.: Dynamic predicate logic. Linguist. Philos. 14, 39–100 (1991)
Groenendijk, J., Stokhof, M., Veltman, F.: Coreference and modality. In: Lappin, S. (ed.) Handbook of Contemporary Semantic Theory, pp. 179–216. Blackwell, Oxford (1996)
Hausser, R., Zaefferer, D.: Questions and answers in a context-dependent Montague grammar. In: Guenthner, F., Schmidt, S.J. (eds.) Formal Semantics and Pragmatics for Natural Languages, pp. 339–358. Reidel, Dordrecht (1978)
Hella, L., Luosto, K., Sano, K., Virtema, J.: The expressive power of modal dependence logic. In: Kooi, R.G.B., Kurucz, A. (eds.) Advances in Modal Logic (AIML), pp. 294–312. College Publications, London (2014)
Henkin, L.: Some remarks on infinitely long formulas. In: Infinitistic Methods. Proceedings of the Symposium on the Foundations of Mathematics, pp. 167–183. Pergamon, New York (1961)
Hintikka, J.: Knowledge and belief: an introduction to the logic of the two notions. Cornell University Press, 1962.
Hintikka, J., Sandu, G.: Game-theoretical semantics. In: Handbook of Logic and Language, pp. 361–410. Elsevier, Amsterdam (1997)
Hodges, W.: Compositional semantics for a language of imperfect information. Log. J. IGPL 5(4), 539–563 (1997)
Hodges, W.: Some strange quantifiers. In: Structures in Logic and Computer Science. Lecture Notes in Computer Science, pp. 51–65. Springer, New York (1997)
Mascarenhas, S.: Inquisitive semantics and logic. Master Thesis, University of Amsterdam (2009)
Roelofsen, F.: Algebraic foundations for the semantic treatment of inquisitive content. Synthese 190(1), 79–102 (2013)
Scha, R.: Logical foundations for question answering. Ph.D. thesis, University of Groningen (1983)
ten Cate, B., Shan, C.C.: Axiomatizing Groenendijk’s logic of interrogation. In: Aloni, M., Butler, A., Dekker, P. (eds.) Questions in Dynamic Semantics, pp. 63–82. Elsevier, New York (2007)
Tichy, P.: Questions, answers, and logic. Am. Philos. Q. 15, 275–284 (1978)
Troelstra, A., van Dalen, D.: Constructivism in Mathematics, An Introduction, vol. 1. Studies in Logic and the Foundations of Mathematics, vol. 121. North-Holland, Amsterdam (1988)
Väänänen, J.: Dependence Logic: A New Approach to Independence Friendly Logic. Cambridge University Press, Cambridge (2007)
Väänänen, J.: Modal dependence logic. In: Apt, K., van Rooij, R. (eds.) New Perspectives on Games and Interaction. Amsterdam University Press, Amsterdam (2008)
Väänänen, J.: Multiverse set theory and absolutely undecidable propositions. In: Kennedy, J. (ed.) Interpreting Gödel: Critical Essays, Cambridge University Press, p. 180 (2014)
Velissaratou, S.: Conditional questions and which-interrogatives. M.Sc. Thesis, University of Amsterdam (2000)
Veltman, F.: Data semantics. In: Groenendijk, J., Janssen, T., Stokhof, M. (eds.) Formal Methods in the Study of Language. Mathematical Centre, Amsterdam (1981)
Veltman, F.: Defaults in update semantics. J. Philos. Log. 25(3), 221–261 (1996)
Yang, F.: On extensions and variants of dependence logic: a study of intuitionistic connectives in the team semantics setting. Ph.D. thesis, University of Helsinki (2014)
Acknowledgements
I am indebted to Lucas Champollion, Jeroen Groenendijk, Lauri Hella, Rosalie Iemhoff, Juha Kontinen, Vít Punčochář, Floris Roelofsen, and Fan Yang for stimulating discussion of the ideas presented here. A special thanks is owed to Jouko Väänänen for bringing together in two separate occasions the communities working on Dependence Logic and Inquisitive Semantics. The present paper has grown out of ideas sparked by those meetings. Financial support from the Netherlands Organization of Scientific Research (NWO) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
Proof of Proposition 22.
We first observe one basic property of our system. Replacement of equivalents:for all formulas \(\varphi,\psi,\chi \in \mathcal{L}\), ψ ⊣ ⊢ χ implies \(\;\varphi [\psi /p] \dashv \vdash \varphi [\chi /p]\).
This claim can be established straightforwardly by induction on φ. Equipped with this observation, we will proceed to prove Proposition 22by induction on φ. If φis an atom or ⊥ , then \(\mathcal{R}(\varphi ) =\{\varphi \}\)and the claim is trivially true. Let us now assume the claim holds for φand ψ, that is, let us assume

and

, and let us proceed to prove that it also holds for φ∧ψ, φ → ψ, φ∨ψ, and

.
-
φ∧ψ. By induction hypothesis and replacement of equivalents, we have

Proposition 21ensures that any entailment pattern which is valid in intuitionistic logic is also valid in QD FO , when

is interpreted as intuitionistic In particular, this ensures that the distributivity of ∧ over
is

is provable. We thus have

Given that \(\mathcal{R}(\varphi \wedge \psi ) =\{\alpha \wedge \beta \,\vert \,\alpha \in \mathcal{R}(\varphi )\text{ and }\beta \in \mathcal{R}(\psi )\}\), the latter formula is nothing but

.
-
φ → ψ. By induction hypothesis and replacement of equivalents, we have

By reasoning intuitionistically with →, ∧ and

we then have

Now, for any \(\alpha \in \mathcal{R}(\varphi )\), we have

The right-to-left direction holds by simple intuitionistic reasoning, while the left-to-right direction simply amounts to the Split rule of our system (recall that resolutions are classical formulas, so this rule is indeed applicable). By replacement of equivalents, we then have the following:
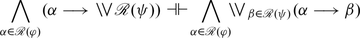
Finally, using again the distributivity of ∧ over

we get that the right-hand side is provably equivalent with the following formula:

Given that \(\mathcal{R}(\varphi \longrightarrow \psi ) =\{\bigwedge _{\alpha \in \mathcal{R}(\varphi )}\alpha \longrightarrow f(\alpha )\,\vert \,f: \mathcal{R}(\varphi )\longrightarrow \mathcal{R}(\psi )\}\), the latter formula is nothing but

.
-
φ∨ψ. By induction hypothesis and replacement of equivalents, we have

Notice that we have

: the left-to-right direction of this equivalence is obtained by an application of the rule (∨d) of our system, while the right-to-left direction is easily proved using the rules

,

(∨r).
Also, notice that by using the rule (∨c), we can make sure that distributivity holds not only on the right side of a tensor, but also on the left side. Then, multiple applications of distributivity on both sides of the tensor yield

Given that \(\mathcal{R}(\varphi \vee \psi ) =\{\alpha \vee \beta \,\vert \,\alpha \in \mathcal{R}(\varphi )\text{ and }\beta \in \mathcal{R}(\psi )\}\), the formula on the right is nothing but

.
-

. By induction hypothesis and replacement of equivalents we have

Given that

, the above formula is simply

.
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Ciardelli, I. (2016). Dependency as Question Entailment. In: Abramsky, S., Kontinen, J., Väänänen, J., Vollmer, H. (eds) Dependence Logic. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-31803-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-31803-5_8
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-31801-1
Online ISBN: 978-3-319-31803-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)