Abstract
The notion of tangential cover, based on maximal segments, is a well-known tool to study the geometrical characteristics of a discrete curve. However, it is not adapted to noisy digital contours. In this paper, we propose a new notion, named Adaptive Tangential Cover, to study noisy digital contours. It relies on the meaningful thickness, calculated at each point of the contour, which permits to locally estimate the noise level. The Adaptive Tangential Cover is then composed of maximal blurred segments with appropriate widths, deduced from the noise level estimation. We present a parameter-free algorithm for computing the Adaptive Tangential Cover. Moreover an application to dominant point detection is proposed. The experimental results demonstrate the efficiency of this new notion.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
For more than ten years, the notion of maximal segment has been widely used in discrete geometry to analyze the contour of digital shapes. Based on the definition of discrete line [15], the sequence of all maximal segments along a digital contour C is called the tangential cover and a very interesting property is that it can be computed in O(N) time complexity [4].
In [5], F. Feschet studies the structure of discrete curves with tangential cover and shows that the tangential cover has the property of being unique and canonical when computed on closed curves. Tangential cover and maximal segments induce numerous discrete geometric estimators (see [9] for a state of the art): length, tangent, curvature estimators, detection of convex or concave parts of a curve, minimum length polygon of a digital contour, detection of the noise level possibly damaging the shape [6, 7], \(\ldots \)
However, the tangential cover is not adapted to noisy digital contours. To deal with this issue, several approaches [3, 16, 17] have been proposed to obtain a better model of tangent cover, adapted to noise. One of them consists in using the notion of maximal blurred segments (MBS) which is an extension of maximal segments with a width parameter [3, 11]. It was used in several geometric estimators: curvature estimator [11], dominant point detection [10, 13], circularity detection, arc and segment decomposition [12, 14], \(\ldots \) Nevertheless, the width parameter needs to be manually adjusted and the method is not adaptive to local amount of noise which can appear on real contours.
In this paper, we propose a new notion, named Adaptive Tangential Cover (ATC), to study noisy digital contours. An ATC of a digital contour is composed of MBS with appropriated widths, deduced from the noise level detected in the contour. The meaningful thicknesses [8], local noise estimation at each point of the discrete contour, permits to determine the widths of MBS composing the ATC. Therefore the algorithm to compute ATC is parameter-free. We apply the ATC to dominant point detection [10] and present experimentations showing the interest of this new notion.
The paper is organized as follows: in Sect. 2, we recall definitions and results used in this paper about blurred segments and meaningful thickness. Then, in Sect. 3, we introduce the ATC definition associated to the meaningful thickness (\(ATC_{MT}\)) and illustrate its construction algorithm. In Sect. 4, an application and experimental results are presented.
2 Geometrical Tools for Discrete Curves Analysis
We recall in this section several notions of discrete geometry, very useful in the study of discrete curves. The main ideas of previous works are presented here and we refer the reader to the given references for more details.
2.1 Maximal Blurred Segments
As previously described, the discrete primitives as discrete lines [15], blurred segments [3] and maximal blurred segments [11] have been used in numerous works to determine geometrical characteristics of discrete curves.
Definition 1
A discrete line \({\mathcal D}(a,b,\mu ,\omega )\), with a main vector (b, a), a lower bound \(\mu \) and an arithmetic thickness \(\omega \) (with a, b, \(\mu \) and \(\omega \) being integer such that \(gcd(a,b)=1\)) is the set of integer points (x, y) verifying \(\mu \le ax -by < \mu +\omega \). Such a line is denoted by \({\mathcal D}(a,b,\mu ,\omega )\).
Let us consider \(\mathcal {S}_f\) as a sequence of integer points.
Definition 2
A discrete line \(\mathcal {D}(a,b,\mu ,\omega )\) is said to be bounding for \(\mathcal {S}_f\) if all points of \(\mathcal {S}_f\) belong to \(\mathcal {D}\).
Definition 3
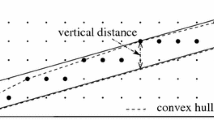
A bounding discrete line \(\mathcal {D}(a,b,\mu ,\omega )\) of \(\mathcal {S}_f\) is said to be optimal if the value \(\frac{\omega -1}{max(|a|,|b|)}\) is minimal, i.e. if its vertical (or horizontal) distance is equal to the vertical (or horizontal) thickness of the convex hull of \(\mathcal {S}_f\).
This definition is illustrated in Fig. 1 and leads to the definition of the blurred segments.
Definition 4
A set \(\mathcal {S}_f\) is a blurred segment of width \(\nu \) if its optimal bounding line has a vertical or horizontal distance less than or equal to \(\nu \) i.e. if \(\frac{\omega -1}{max(|a|,|b|)}\le \nu \).
The notion of maximal blurred segment was introduced in [11]. Let C be a discrete curve and \(C_{i,j}\) a sequence of points of C indexed from i to j. Let us suppose that the predicate “\(C_{i,j}\) is a blurred segment of width \(\nu \)” is denoted by \(BS(i,j,\nu )\).
Definition 5
\(C_{i,j}\) is called a maximal blurred segment of width \(\nu \) and noted \(MBS(i,j,\nu )\) iff \(BS(i,j,\nu )\), \(\lnot BS(i,j+1,\nu )\) and \(\lnot BS(i-1,j,\nu )\).
The following important property was proved:
Property 1
Let \(MBS_{\nu }(C)\) be the set of width \(\nu \) maximal blurred segments of the curve C. Then, \(MBS_{\nu }(C)=\{MBS(B_0,E_0,\nu )\), \(MBS(B_1,E_1,\nu )\),..., \( MBS(B_{m-1},E_{m-1},\nu )\}\) and satisfies \(B_0 < B_1 < \ldots < B_{m-1}\). So we have: \(E_0 < E_1 < \ldots < E_{m-1}\).
Deduced from the previous property, an incremental algorithm was proposed in [11] to determine the set of all maximal blurred segments of width \(\nu \) of a discrete curve C. The main idea is to maintain a blurred segment when a point is added (or removed) to (from) it. The obtained structure for a given width \(\nu \) can be considered as an extension of the tangential cover [4] and we name it width \(\nu \) tangential cover of C. Examples of tangential covers for different widths are given in Fig. 5(c–f).
2.2 Meaningful Thickness
In [6, 7], a notion, called meaningful scale, was designed to locally estimate what is the best scale to analyze a digital contour. This estimation is based on the study of the asymptotic properties of the discrete length L of maximal segments. In particular, it has been shown that the lengths of maximal segments covering a point P located on the boundary of a \(C^3\) real object should be between \(\varOmega (1/h^{1/3})\) and \(O(1/h^{1/2})\) if P is located on a strictly concave or convex part and near O(1 / h) elsewhere (where h represents the grid size). This theoretical property defined on finer and finer grid sizes was used by taking the opposite approach with the computation of the maximal segment lengths obtained with coarser and coarser grid sizes (from subsampling). Such a strategy is illustrated on figure Fig. 2(a–c) with a source point P and its tangential cover defined from subsampling grid size equals to 2 (image (b)) and 3 (image (c)). From the graph of the maximal segment mean lengths \(\overline{L^i}\) obtained at different scales, the method consists in recognizing the maximal scale for which the lengths follow the previous theoretical behavior.
Images (a–c) illustrate the maximal segments (with their mean discrete length \(\overline{L}\)) used in the meaningful scale estimation computed by subsampling the initial contour (a). The equivalent blurred segments defined with different thicknesses illustrate the primitives used in the notion of meaningful thickness (d–f). The mean lengths \(\overline{\mathcal {L}^k}\) of the blurred segments are given for each thickness/width k.
The previous method of meaningful scale detection [6, 7] has been extended to the detection of the meaningful thickness (MT) [8]. This method mainly differs by the choice of the blurred segment primitive and by the scale definition which is given by the thickness/width parameter of the blurred segment. Such a strategy presents the first advantage to be easier to implement without the need to apply different subsamplings.
The length variation of the maximal blurred segments obtained at different thicknesses/widths follows the equivalent properties than for the maximal segment defined from sub-sampling. Figure 3 shows the comparison of the length variations obtained with the maximal segments (b) and the maximal blurred segments (c). In the two cases, the evolution of lengths presents equivalent slopes which are included in the same interval. More formally, if we denote by \(t_i\) the thickness of value i, a multi-thickness profile \(\mathcal {P}_{n}(P)\) of a point P is defined as the graph \((\log (t_i),\log (\overline{\mathcal {L}}^{t_i}/t_i))_{i=1,\dots ,n}\). The following property has been experimentally checked.
Property 2
(Multi-thickness). The plots of the lengths \(\mathcal {L}_j^{t_i}/t^i\) in log-scale are approximately affine with negative slopes s located between \({-}\frac{1}{2}\) and \({-}\frac{1}{3}\) for a curved part and around \(-1\) for a flat part.
Such a profile is illustrated on Fig. 4(a), (b) where a multi-thickness profile is given on a point located on a contour part presenting no noise.
Multi-thickness profiles (b–d) obtained on different points: \(P_j\) with no noise (graph (b)), with low noise (\(P_k\), graph (c)) and important noise (\(P_l\), graph (d)). The meaningful thickness \(\eta _j\), \(\eta _k\) and \(\eta _l\) are represented on each multi-thickness profile \(\mathcal {P}_{15}\) (Color figure online).
From the multi-thickness profile, a meaningful thickness is defined as a pair \((i_1,i_2)\), \(1 \le i_1 < i_2 \le n \), such that for all i, \(i_1 \le i < i_2\), \(\frac{Y_{i+1}-Y_i}{X_{i+1}-X_i} \le T_m\), and the property is not true for \(i_1 - 1\) and \(i_2\). As suggested in [8], the value of the parameter \(T_m\) is set to 0. In the following, we will denote by \(\eta _j\) the first meaningful thickness (\(i_1\)) of a point \(P_j\). Figure 4 illustrates the meaningful thickness obtained for different types of point \(P_j\), \(P_k\) and \(P_l\) which present respectively the following thicknesses: \(\eta _j=1\), \(\eta _k=3\) and \(\eta _l=5\). Another illustration of meaningful thickness result is proposed in Fig. 5(b).
This notion is used in the next section to define an adaptive tangential cover by taking into account the amount of noise on the curve.
Illustration of Algorithm 1. (a) Input discrete curve C. (b) Noise level at each point \(C_i\) of C detected by meaningful thickness method; the red, green and violet points correspond to the meaningful thickness \(\eta _i\) of 1, 2 and 3 respectively. The label of each point \(C_i\) is initialized by its corresponding \(\eta _i\). (c) Tangential covers of three different widths \(\nu _k =\) 1, 2 and 3 in yellow, blue and cyan. (d) (e) and (f) Labeling all points \(C_i\) of C in function of its meaningful thickness and the tangent covers of widths 1, 2 and 3 respectively; The label \(\gamma _i\) of each point \(C_i\) is updated to \(\nu _k\) if the maximal meaningful thickness, namely \(\alpha \), of points that belong to the \(MBS(B_i,E_i,\nu _k)\) passing by \(C_i\) is equal to \(\nu _k\), and stayed as \(\gamma _i\) otherwise. (g) Label \(\gamma _i\) associated to each point of the considering curve. (h) Adaptive tangential cover obtained from the tangential covers and the labels of points (Color figure online).
3 Adaptive Tangential Cover
The tangential covers applied for dominant point [10] and arc/circle detection [14] use mostly mono-width value, denoted by \(\nu _1\). Such a parameter \(\nu _1\) allows to take into account the amount of noise present in digital contours. This method has two drawbacks. Firstly, the value of \(\nu _1\) is manually adjusted in order to obtain a relevant approximating polygon of the contours w.r.t. the noise. Secondly, the noise appearing along the contour can be random. In other words, different noise levels can be presented along the contours. Figure 5(b) illustrates the different noise levels detected by the meaningful thickness method. Thus, using mono-width value for tangential covers is inadequate in case of noisy curves.
To overcome these issues, we present the definition of adaptive tangential cover which is a tangential cover with different width values. To this end, we first introduce the notion of inclusion of two MBS.
Definition 6
Let C be a discrete curve and \(MBS_i = MBS(B_i,E_i,.)\), \(MBS_j = MBS(B_j,E_j,.)\) two distinct maximal blurred segments on C. \(MBS_j\) is said to be included in \(MBS_i\) if \(B_i\le B_j\) and \(E_i \ge E_j\), and noted by \(MBS_j \subseteq MBS_i\).
Definition 7
Let MBS(C) be a set of maximal blurred segment of a discrete curve C. \(MBS_i = MBS(B_i,E_i) \in MBS(C) \) is said largest if for all \(MBS_j \in MBS(C)\) with \(i \ne j\), \(MBS_j \nsubseteq MBS_i\).
Definition 8
Let \(C = ( C_i )_{0\le i \le n-1}\) be a discrete curve. Let \(\eta = (\eta _i )_{0\le i \le n-1}\) be the vector of meaningful thickness associated to each \(C_i\) of C. Let \(MBS(C) =\{MBS_{\nu _k}(C)\}\) be the sets of MBS for the different values \(\nu _k\) in \(\eta \). An adaptive tangential cover associated to meaningful thickness (\(ATC_{MT}\)) of C is defined as the set of the largest MBS of \(\big \{ MBS_j=MBS(B_j,E_j,v_k) \in MBS(C) \mid v_k = \max \{ \eta _t \mid t \in [\![ B_j, E_j ]\!]\} \big \}\).
As stated in Sect. 2.2, the method of meaningful thickness allows to prevent/estimate locally the noise level at each point of the discrete contour. Such a framework is thus integrated in the construction of \(ATC_{MT}\) to provide the information of noise along the contour. More precisely, the \(ATC_{MT}\) contains the MBS with width values varying in function of the perturbations obtained by the meaningful thickness values. Since the noise levels are different along the contour curve, accordingly, the obtained \(ATC_{MT}\) has the MBS with bigger width values at noisy zones, and with smaller width values in zones with less or no noise (see Fig. 5(h)). Furthermore, this framework is parameter-free. The method for computing \(ATC_{MT}\) is described in Algorithm 1. This algorithm is divided into two steps: (1) labelling the point from the meaningful thickness values, and (2) building the \(ATC_{MT}\) of the curve from the labels previously obtained.
More precisely, the algorithm is initialized with an empty \(ATC_{MT}\) and the labels associated to each point are the same as meaningful thickness values (Lines 2–3). In the first step (Lines 4–8), the tangential covers with widths corresponding to all different noise levels are examined in order to find the label of each point. At each level \(\nu _k\), the label of a point is updated to \(\nu _k\) if the MBS passing through the point has the maximal meaningful thickness being equal to \(\nu _k\). It should be noted that the number of noise levels overall the contour is much smaller than the number of points on the contour. Thus, the number of considered tangential covers is often small. Then, in the second step (Lines 9–12), the \(ATC_{MT}\) is composed of the MBS with widths being the label associated to points constituting the MBS. An illustration of the algorithm is given in Fig. 5.

4 Application to Dominant Point Detection
Tangential covers, as stated previously, are involved in applications of dominant point detection [10]. The previous approaches use tangential covers composed of maximal blurred segments with a constant width along the curve. Such a width allows a flexible segmentation of discrete curves with respect to the noise. In general, this parameter needs to be manually adjusted to obtain a good result of detection algorithm. Therefore, such approaches are not adaptive to discrete contours with irregular noise.

Illustration of Algorithm 2 with the adaptive tangential cover obtained by Algorithm 1 in Fig. 5. Considering the maximal blurred segments \(MBS(C_{69},C_{189},2)\), \(MBS(C_{164},C_{191},2)\) and \(MBS(C_{186},C_{235},3)\), the common zone determined by these three segments are four points: \(C_{186},C_{187},C_{188}\) and \(C_{189}\) (green and red points in the zoom). The left and right extremities of the common zone are \(C_{69}\) and \(C_{235}\) respectively. The angle between each point in the common zone and the two extremities are respectively \(102.708^{\circ }\), \(101.236^{\circ }\), \(99.7334^{\circ }\) and \(100.817^{\circ }\). The dominant point is the point having the smallest angle measure, i.e., \(C_{188}\) (red point in the zoom) (Color figure online).
In this section, we present a dominant point detection algorithm using \(ATC_{MT}\). The reason is twofold: (1) the \(ATC_{MT}\) takes into account the amount of noise on the curve and thus allows a better model of curve segmentation, and (2) the algorithm for computing \(ATC_{MT}\) is parameter-free.
4.1 Dominant Point Detection Algorithm
The algorithm for dominant point detection proposed in this section is the same as the one presented by [10]. It should be mentioned that the modified part is to use an \(ATC_{MT}\) instead of a classical tangential cover with mono-width for segmenting the digital curve. The algorithm consists in first finding the candidates of dominant points in the smallest common zone induced by successive maximal blurred segments. Then, the dominant point of each common zone is identified as the point having the smallest angle with the two extremities of the left and right of the maximal blurred segments composing the zone. The algorithm is described in Algorithm 2, and illustrated in Fig. 6.
4.2 Experimentations
In this section, we present experimental results of the dominant point detection algorithm using the proposed notion of \(ATC_{MT}\). In order to compare the current parameter-free method, we consider in our experiments the mean tangential cover with MBS of width-\(\overline{\eta }\) equals to the average of the obtained meaningful thicknesses at each point of the studied curve. In fact, this width-\(\overline{\eta }\) parameter was proposed and used in [14].
The experiments are carried out on both data with and without noise. From Figs. 7 and 8, it can be seen that using the mean tangential cover is not always a relevant strategy, particularly in the high noisy zones of curves. This is due to the fact that the width-\(\overline{\eta }\) parameter could not capture the local noise on curve, contrary to the \(ATC_{MT}\) method (see Figs. 7 and 8(b),(d)).
In Fig. 8(a), (c), the flower curve seems to be a discrete curve without noise. Though, the meaningful thickness method detects two noise levels, 1 and 2 (see the zooms in Fig. 8(c)). In the 2-meaningful thickness zones, the dominant point detection with \(ATC_{MT}\) method fits better the corners, whereas the mean method induces a decomposition very close to the studied curve and detects more dominant points. In other words, in the curved zones, the \(ATC_{MT}\) method simplifies the representation of the curve.
5 Conclusion and Perspectives
We present in this paper a new notion, the Adaptive Tangential Cover deduced from the meaningful thickness. The obtained decomposition in MBS of various widths transmits the noise levels and the geometrical structure of the given discrete curve. Moreover the method to compute the ATC is parameter free. An online demonstration based on the DGtal [1] and ImaGene [2] library, is available at the following website:
http://ipol-geometry.loria.fr/~kerautre/ipol_demo/ATC_IPOLDemo/
The ATC is used in a dominant point detection algorithm and permits to obtain a parameter-free method with very good results on the polygonal shapes with or without noise. For the shapes with convex and/or concave parts, the algorithm simplifies the shapes in a polygonal way.
In this article, we have considered the ATC definition based on the notion of the meaningful thickness. In the further work, we may consider the generalization of ATC using other width estimations. The proposed approach opens numerous perspectives, for example the use of ATC in geometric estimators or in the decomposition of a curve in arcs and segments.
References
DGtal: Digital Geometry tools and algorithms library. http://libdgtal.org
Imagene, Generic digital Image library. http://gforge.liris.cnrs.frs/projects/imagene
Debled-Rennesson, I., Feschet, F., Rouyer-Degli, J.: Optimal blurred segments decomposition of noisy shapes in linear time. Comput. Graph. 30(1), 30–36 (2006)
Feschet, F., Tougne, L.: Optimal time computation of the tangent of a discrete curve: application to the curvature. In: Bertrand, G., Couprie, M., Perroton, L. (eds.) DGCI 1999. LNCS, vol. 1568, pp. 31–40. Springer, Heidelberg (1999)
Feschet, F.: Canonical representations of discrete curves. Pattern Anal. Appl. 8(1–2), 84–94 (2005)
Kerautret, B., Lachaud, J.O.: Meaningful scales detection along digital contours for unsupervised local noise estimation. IEEE Trans. Pattern Anal. Mach. Intell. 34(12), 2379–2392 (2012)
Kerautret, B., Lachaud, J.O.: Meaningful scales detection: an unsupervised noise detection algorithm for digital contours. Image Process. On Line 4, 98–115 (2014)
Kerautret, B., Lachaud, J.O., Said, M.: Meaningful thickness detection on polygonal curve. In: Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pp. 372–379. SciTePress (2012)
Lachaud, J.-O.: Digital shape analysis with maximal segments. In: Köthe, U., Montanvert, A., Soille, P. (eds.) WADGMM 2010. LNCS, vol. 7346, pp. 14–27. Springer, Heidelberg (2012)
Ngo, P., Nasser, H., Debled-Rennesson, I.: Efficient dominant point detection based on discrete curve structure. In: Barneva, R.P., et al. (eds.) IWCIA 2015. LNCS, vol. 9448, pp. 143–156. Springer, Heidelberg (2015)
Nguyen, T.P., Debled-Rennesson, I.: On the local properties of digital curves. Int. J. Shape Model. 14(2), 105–125 (2008)
Nguyen, T.P., Debled-Rennesson, I.: Decomposition of a curve into arcs and line segments based on dominant point detection. In: Heyden, A., Kahl, F. (eds.) SCIA 2011. LNCS, vol. 6688, pp. 794–805. Springer, Heidelberg (2011)
Nguyen, T.P., Debled-Rennesson, I.: A discrete geometry approach for dominant point detection. Pattern Recogn. 44(1), 32–44 (2011)
Nguyen, T.P., Kerautret, B., Debled-Rennesson, I., Lachaud, J.-O.: Unsupervised, fast and precise recognition of digital arcs in noisy images. In: Bolc, L., Tadeusiewicz, R., Chmielewski, L.J., Wojciechowski, K. (eds.) ICCVG 2010, Part I. LNCS, vol. 6374, pp. 59–68. Springer, Heidelberg (2010)
Reveillès, J.P.: Géométrie discrète, calculs en nombre entiers et entiersgorithmique, thèse d’état. Université Louis Pasteur, Strasbourg (1991)
Rodríguez, M., Largeteau-Skapin, G., Andres, E.: Adaptive pixel resizing for multiscale recognition and reconstruction. In: Wiederhold, P., Barneva, R.P. (eds.) IWCIA 2009. LNCS, vol. 5852, pp. 252–265. Springer, Heidelberg (2009)
Vacavant, A., Roussillon, T., Kerautret, B., Lachaud, J.: A combined multi-scale/irregular algorithm for the vectorization of noisy digital contours. Comput. Vis. Image Underst. 117(4), 438–450 (2013)
Acknowledgement
The authors would like to thank the reviewers for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Ngo, P., Nasser, H., Debled-Rennesson, I., Kerautret, B. (2016). Adaptive Tangential Cover for Noisy Digital Contours. In: Normand, N., Guédon, J., Autrusseau, F. (eds) Discrete Geometry for Computer Imagery. DGCI 2016. Lecture Notes in Computer Science(), vol 9647. Springer, Cham. https://doi.org/10.1007/978-3-319-32360-2_34
Download citation
DOI: https://doi.org/10.1007/978-3-319-32360-2_34
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-32359-6
Online ISBN: 978-3-319-32360-2
eBook Packages: Computer ScienceComputer Science (R0)