Abstract
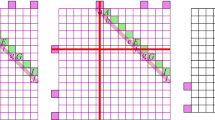
In this paper we present a linear-time and linear-space algorithm for the decomposition of binary images into rectangles. Our contribution is a two-stage algorithm. In the first stage we compute a \({\textstyle \frac{1}{min(h,w)}}\)-approximation for the largest rectangle starting at each point of the matrix. In the second stage the algorithm walks through the matrix, alternatively stacking, merging or removing encountered rectangles. Through an experimental evaluation, we show that our algorithm outperforms state-of-the-art linear-time algorithms for small to medium-sized rectilinear polygons.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Eppstein, D.: Graph-theoretic solutions to computational geometry problems. In: Paul, C., Habib, M. (eds.) WG 2009. LNCS, vol. 5911, pp. 1–16. Springer, Heidelberg (2010)
Ferrari, L., Sankar, P.V., Sklansky, J.: Minimal rectangular partitions of digitized blobs. Comput. Graph. Image Process. 28(1), 58–71 (1984)
Gao, D., Wang, Y.: Decomposing document images by heuristic search. In: Yuille, A.L., Zhu, S.-C., Cremers, D., Wang, Y. (eds.) EMMCVPR 2007. LNCS, vol. 4679, pp. 97–111. Springer, Heidelberg (2007)
Gonzalez, T., Zheng, S.-Q.: Bounds for partitioning rectilinear polygons. In: 1st Symposium on Computational Geometry, pp. 281–287. ACM (1985)
Levcopoulos, C.: Improved bounds for covering general polygons with rectangles. In: Nori, K.V. (ed.) Foundations of Software Technology and Theoretical Computer Science. LNCS, vol. 287, pp. 95–102. Springer, Heidelberg (1987)
Lingas, A., Pinter, R.Y., Rivest, R.L., Shamir, A.: Minimum edge length partitioning of rectilinear polygons. In: Proceeding of 20th Allerton Conference Communication Control and Computing, pp. 53–63 (1982)
Liou, W.T., Tan, J.J., Lee, R.C.: Minimum partitioning simple rectilinear polygons in o (n log log n)-time. In: Proceedings of the Fifth Annual Symposium on Computational Geometry, pp. 344–353. ACM (1989)
Lipski, W., Lodi, E., Luccio, F., Mugnai, C., Pagli, L.: On two dimensional data organization ii. Fundamenta Informaticae 2(3), 245–260 (1979)
Nahar, S., Sahni, S.: Fast algorithm for polygon decomposition. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 7(4), 473–483 (1988)
Ohtsuki, T.: Minimum dissection of rectilinear regions. In: Proceeding IEEE Symposium on Circuits and Systems, Rome, pp. 1210–1213 (1982)
Rocher, P.-O., Gravier, C., Subercaze, J., Preda, M.: Video stream transmodality. In: Cordeiro, J., Hammoudi, S., Maciaszek, L., Camp, O., Filipe, J. (eds.) ICEIS 2014. LNBIP, vol. 227, pp. 361–378. Springer, Heidelberg (2015)
Soltan, V., Gorpinevich, A.: Minimum dissection of a rectilinear polygon with arbitrary holes into rectangles. Discrete Comput. Geom. 9(1), 57–79 (1993)
Spiliotis, I.M., Mertzios, B.G.: Real-time computation of two-dimensional moments on binary images using image block representation. IEEE Trans. Image Process. 7(11), 1609–1615 (1998)
Suk, T., Höschl IV, C., Flusser, J.: Decomposition of binary images a survey and comparison. Pattern Recogn. 45(12), 4279–4291 (2012)
Tomás, A.P., Bajuelos, A.L.: Generating Random Orthogonal Polygons. In: Conejo, R., Urretavizcaya, M., Pérez-de-la-Cruz, J.-L. (eds.) CAEPIA/TTIA 2003. LNCS (LNAI), vol. 3040, pp. 364–373. Springer, Heidelberg (2004)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Subercaze, J., Gravier, C., Rocher, PO. (2016). A Merging Heuristic for the Rectangle Decomposition of Binary Matrices. In: Goldberg, A., Kulikov, A. (eds) Experimental Algorithms. SEA 2016. Lecture Notes in Computer Science(), vol 9685. Springer, Cham. https://doi.org/10.1007/978-3-319-38851-9_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-38851-9_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-38850-2
Online ISBN: 978-3-319-38851-9
eBook Packages: Computer ScienceComputer Science (R0)