Abstract
In the setting of contract theory, retractable contracts have been defined to formalize binary session protocols where the partners can go back to certain particular synchronization points when the session gets stuck, looking for a successful state, if any.
In the present paper we propose a three-party game-theoretic interpretation of client/server systems of retractable contracts. In particular, we show that a client is retractable-compliant with a server if and only if there exists a winning strategy for a particular player in a game-theoretic model of contracts. Such a player can be looked at as a mediator, driving the choices in the retractable points. We show that winning strategies for the mediator player correspond to orchestrators in a system of orchestrated client/server sessions, and vice versa.
This work was partially supported by the COST Action IC1405 of the European Union and by the Project FIR 1B8C1 of the University of Catania.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
The notion of contract has been proposed as an abstraction to formally specify and check the behaviour of software systems, and especially of web services. In particular, in the setting of service-oriented architectures the concept of agreement, often called compliance, is of paramount importance while searching components and ensuring that they will properly collaborate with each other. The main challenge is that compliance has to meet the contrasting requirements of guaranteeing correctness of interactions w.r.t. certain safety and liveness conditions, while remaining coarse enough to maximize the possibilities of finding compliant components in a library or services through the web.
The main conceptual tool to face the issue is that of relaxing the constraint of a perfect correspondence among contracts through contract refinement, also called sub-contract [8, 9] and sub-behaviour [3] relations, that is pre-order relations such that processes conforming to more demanding contracts (which are lower in the pre-order) can be safely substituted in contexts allowing more permissive ones. Indeed contract refinement closely resembles subtyping, as it is apparent in the case of session types [3, 10], and it is related to (but doesn’t coincide with) observational pre-orders and must-testing in process algebra [6, 11].
However, since the first contributions to the theory of contracts [9], a rather different approach has been followed, based on the idea of filtering out certain actions that, although unmatched on both sides of a binary interaction, can be neglected or prevented by the action of a mediating process called the orchestrator [13, 14], without compromising the reaching of the goals of the participants, like the satisfaction of all client requests in a client-server architecture.
An alternative route for the same purpose is to change the semantics of contracts so that interacting processes can adapt each other by means of a rollback mechanism: these are the retractable contracts proposed in [4]. Although compliance can be decided in advance, interaction among processes exposing retractable contracts undergoes a sequence of failures and backtracks that might be avoided by extracting information from the compliance check.
The contribution of the present paper is to show that the two approaches of orchestrated and retractable compliance are indeed equivalent, at least in the case of session contracts (see [2, 3], where they are dubbed “session behaviours”), which are contracts that limit the non-determinism by constraining both external and internal choices to a more regular form. More precisely, we consider contracts that are syntactically the same as retractable ones, but instead of adding rollback to the usual contract semantics, we abstractly define outputs in an external choice as affectible actions: their actual sent can be influenced by the partner in a binary session or by some entity external to the system. Affectible actions correspond to retractable actions in [4].
The essence of the construction is that (an appropriate restriction of) orchestrators correspond to winning strategies in certain concurrent games that naturally model retractable contracts. In [5] the theory of contracts has been grounded on games over event structures among multiple players; applying this framework to retractable contracts, the interaction among a client and a server can be seen as a play in a three-party game. Player \(\mathsf A\) moves according to the unaffectible actions of the client; player \(\mathsf B\) moves according to the unaffectible actions of the server, whereas moves by player \(\mathsf C\) correspond to affectible actions on both sides, namely the retractable agreement points of the system. The client \(\rho \) is hence affectible-compliant with the server \(\sigma \) whenever \(\mathsf C\) has a winning strategy in the game with players \(\mathsf A\) and \(\mathsf B\), where player \(\mathsf C\) wins when she succeeds to lead the system \(\rho \Vert \sigma \) to a successful state (the client terminates) or the interaction proceeds indefinitely without deadlocking.
The payoff of the game theoretic interpretation is that there is a precise correspondence between winning strategies for player \(\mathsf C\) and elements of a class of orchestrators in the sense of [14]. Such a correspondence is of interest on its own, since strategies are abstract entities while orchestrators are terms of a process algebra and concrete witnesses of the agreement among participants of a session. Moreover, we can decide whether a client-server pair is reversible-compliant by means of an algorithm that synthesizes an orchestrator if any, or reports failure.
1 Affectible Contracts and Retractable Compliance
Affectible session contracts (affectible contracts for short) are a variant of retractable contracts in [4]; they are syntactically the same, but affectible session contracts have a different, and more abstract semantics. Nonetheless compliance coincides in both settings as we show in this section.
Definition 1
(Affectible session contracts). Let \(\mathcal{N}\) (set of names) be some countable set of symbols and let \(\overline{\mathcal{N}}= \{\,\overline{a} \mid a \in \mathcal{N}\,\}\) (set of conames), with \(\mathcal{N}\cap \overline{\mathcal{N}}= \emptyset \). The set \(\mathsf {A\!S\!C}\) of affectible session contracts is defined as the set of the closed (with respect to the binder \(\mathsf{rec} \, \)) expressions generated by the following grammar,
where I is non-empty and finite, the names and the conames in choices are pairwise distinct and \(\sigma \) is not a variable in \(\mathsf{rec} \, x.\sigma \).
Affectible as well as retractable contracts stem from session behaviours of [3] also called session contracts in [6]. With respect to session behaviors, affectible contracts add the affectible output construct, which is called retractable output in [4]. The affectible output represents points where the client-server interaction can be influenced by the partner process, or can be guided by a third party; consequently they are represented by the CCS external choice operator as it is the case of the input branching (which is always affectible). Outputs in an internal choice are regarded as unaffectible actions and treated as unretractable in the setting of retractable contracts. The transitions representing an internal choice have no label; note that any \(\bigoplus _{i\in I} \overline{a}_i.\sigma _i\) just reduces to one of its summands.
In the following we consider recursion up-to unfolding, that is we equate \(\mathsf{rec} \, x .\sigma \) with \(\sigma \{x/\mathsf{rec} \, x .\sigma \}\). The symbol \(\alpha \) will be used as a variable ranging over \(\mathcal{N}\cup \overline{\mathcal{N}}\).
Definition 2
(LTS for \(\mathsf {A\!S\!C}\) ). Let \(\mathbf{{Act}} = \mathcal{N}\cup \overline{\mathcal{N}}\cup \{\,\overline{a}^+\mid \overline{a}\in \overline{\mathcal{N}}\,\}\).
A client/server system (system for short) is a pair of contracts in \(\mathsf {A\!S\!C}\) that we denote by \(\rho \,\Vert \,\sigma \).
Definition 3
(LTS for systems). Let \(\mathbf{csAct} = \{\,+,\tau \,\}\).

We define \(\mathrel {\mathop {\Longrightarrow }\limits ^{}} \,=\, \mathrel {\xrightarrow {\,\,}{\!\!^*}}\circ \mathrel {\xrightarrow {\,\tau \,}{}}\) and \(\mathrel {\mathop {\Longrightarrow }\limits ^{+}} \,=\, \mathrel {\xrightarrow {\,\,}{\!\!^*}}\circ \mathrel {\xrightarrow {\,+\,}{}}\). In the last rule, \(\overline{\alpha }\) is the CCS involution of names and co-names.
The semantics of \(\rho \,\Vert \,\sigma \) is reminiscent of CCS parallel composition as used to define testing preorders in [12], but for the usage of the labels \(+\) and \(\tau \) and for the absence of a success marker (there is a set of success states instead: see below). We use labels \(+\) and \(\tau \) to distinguish among affectible and unaffectible communications respectively, although they are both unobservable as the only observable facts are termination and the resulting state.
Lemma 1
Let \(\rho ,\sigma \in \mathsf {A\!S\!C}\). \(\rho \,\Vert \,\sigma \mathrel {\mathop {\Longrightarrow }\limits ^{}}\) and \(\rho \,\Vert \,\sigma \mathrel {\mathop {\Longrightarrow }\limits ^{+}}\) can never both occur.
The affectible compliance relation can be now coinductively defined as follows.
Definition 4
(Affectible Compliance Relation \(\dashv ^{{\tiny {\mathsf{A}}}}\) ).
-
(i)
Let \(\mathcal{H}: \mathcal{P}(\mathsf {A\!S\!C}\times \mathsf {A\!S\!C})\rightarrow \mathcal{P}(\mathsf {A\!S\!C}\times \mathsf {A\!S\!C})\) be such that, for any
 , we get
, we get  if the following conditions hold:
if the following conditions hold:-
(1)
\([~\rho \,\Vert \,\sigma ~\not \!\!\mathrel {\mathop {\Longrightarrow }\limits ^{}}\) and \(\rho \,\Vert \,\sigma ~\not \!\!\mathrel {\mathop {\Longrightarrow }\limits ^{+}}~]\) implies \(\rho =\mathbf{1}\);
-
(2)
\(\forall \rho ',\sigma ' \). \( [~ \rho \,\Vert \,\sigma \mathrel {\mathop {\Longrightarrow }\limits ^{}} {\rho '}\,\Vert \,{\sigma '}\) implies
 ;
; -
(3)
\(\rho \,\Vert \,\sigma \mathrel {\mathop {\Longrightarrow }\limits ^{+}}\) implies \(\exists \rho ',\sigma '\). \([~\rho \,\Vert \,\sigma \mathrel {\mathop {\Longrightarrow }\limits ^{+}} {\rho '}\,\Vert \,{\sigma '}\) and
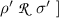 .
.
-
(1)
-
(ii)
A relation
 is an affectible compliance relation if
is an affectible compliance relation if  . \(\dashv ^{{\tiny {\mathsf{A}}}}\) is the greatest solution of the equation \(X=\mathcal{H}(X)\), that is \(\dashv ^{{\tiny {\mathsf{A}}}}~= \nu \mathcal{H}\).
. \(\dashv ^{{\tiny {\mathsf{A}}}}\) is the greatest solution of the equation \(X=\mathcal{H}(X)\), that is \(\dashv ^{{\tiny {\mathsf{A}}}}~= \nu \mathcal{H}\).
In words the client \(\rho \) is affectible-compliant with the server \(\sigma \) if either \(\rho \) and \(\sigma \) cannot communicate because \(\rho = \mathbf{1}\), namely all client requirements have been satisfied; or all unaffectible communications of the system \(\rho \,\Vert \,\sigma \) lead to compliant systems; or there exists an affectible communication leading to a compliant system. By Lemma 1 the last two conditions cannot be simultaneously satisfied.
Because of conditions (i2) and (i3), the affectible compliance relation is an abstract concept; but it can be made concrete via the characterization in terms of retractable computations, provided in Sect. 1.
Let us consider the following example from [4]. A \(\textsf {Buyer}\) is looking for a bag (\(\overline{\mathtt{bag}}\)) or a belt (\(\overline{\mathtt{belt}})\); she will decide how to pay, either by credit card (\(\overline{\mathtt{card}}\)) or by cash (\(\overline{\mathtt{cash}}\)), after knowing the \(\mathtt{price}\) from the \(\textsf {Seller}\).
The \(\mathsf {Seller}\) does not accept credit card payments for items of low price, like belts, but only for more expensive ones, like bags:
From the previous definition it is not difficult to check that \(\textsf {Buyer}\dashv ^{{\tiny {\mathsf{A}}}}\textsf {Seller}\).
Retractable Contracts. Let us recall the formalism of retractable contracts; the following definitions and Theorem 1 below are from [4]. As said before, retractable and affectible contracts are syntactically the same, but the operational semantics of the formers is based on a rollback operation, acting on the recording of certain discarded branches of an interaction. The notion of contracts with histories is defined as follows:
Definition 5
(Contracts with histories). Let \(\mathsf{Histories}\) be the set of expressions (referred to also as stacks) generated by the grammar:
Then the set of contracts with histories is defined by:
Histories are finite lists of contracts representing the branches which have been discarded because of a retractable synchronization action. The effect of retracting such an action is modeled by restoring the last contract on the history as the actual contract and by trying a different branch, if any. This is formalised by the operational semantics of contracts with histories that is defined as follows.
Definition 6
(LTS of Contracts with Histories).
When selecting a branch of an external choice, the discarded branches are memorised on top of the new stack (the last contract of the history) in the right-hand side of rule \((+)\); on the contrary, when an internal choice occurs, the stack remains unchanged in rule (\(\oplus \)). When a single action is executed, the history is modified by adding a ‘\(\circ \)’, meaning that the only available branch has been tried and no alternative is left. Rule \((\mathsf{rb})\) recovers the contract on the top of the stack (if the stack is different than \([\;]\)) by replacing the current one with it. Note that the combined effect of rules (\(\oplus \)) and \((\alpha )\) is that the alternative branches of an internal choice are unrecoverable.
The interaction of a client with a server is modeled by the reduction of their parallel composition, that can be either forward, consisting of CCS style synchronisations and single internal choices, or backward if there is no possible forward reduction, the client is different than \(\mathbf{1}\) (the fulfilled contract) and rule \((\mathsf{rb})\) is applicable on both sides.
Definition 7
(TS of Client/Server Pairs). We define the relation \(\mathrel {\mathop {\longrightarrow }\limits ^{}}\) over pairs of retractable contracts with histories by the following rules:

plus the rule symmetric to \((\tau )\) w.r.t. \(\Vert \). Moreover, rule \(({\textsf {rbk}})\) applies only if neither \(({\textsf {comm}})\) nor \((\tau )\) do.
Up to the rollback mechanism, compliance in the retractable setting is defined as usually done with client/server contracts.
Definition 8
(Retractable Compliance, \(\dashv ^{{\tiny {\mathsf{rbk}}}}\) ).
-
(i)
The relation \(\dashv ^{{\tiny {\mathsf{rbk}}}}\) on contracts with histories is defined as follows:
\({ \ for \ any \ } \varvec{\delta '},\rho ',\varvec{\gamma '},\sigma '\), \(\varvec{\delta }\prec \rho \dashv ^{{\tiny {\mathsf{rbk}}}}\varvec{\gamma }\prec \sigma \) holds whenever
$$\begin{aligned} \varvec{\delta }\prec \rho \,\Vert \,\varvec{\gamma }\prec \sigma \mathrel {\mathop {\longrightarrow }\limits ^{*}} \varvec{\delta '}\prec \rho '\,\Vert \,\varvec{\gamma '}\prec \sigma ' \not \!\!\mathrel {\mathop {\longrightarrow }\limits ^{}} { \ implies \ }\rho '=\mathbf{1}\end{aligned}$$ -
(ii)
The relation \(\dashv ^{{\tiny {\mathsf{rbk}}}}\) on contracts is defined by: \(\rho \dashv ^{{\tiny {\mathsf{rbk}}}}\sigma ~~~~{if}~~~~ [\;]\prec \rho \dashv ^{{\tiny {\mathsf{rbk}}}}[\;]\prec \sigma .\)
In Buyer/Seller example we have that, in case a belt is agreed upon and the buyer decides to pay using her credit card, the system gets stuck in an unsuccessful state. This causes a rollback enabling a successful state to be reached. So \(\textsf {Buyer}\dashv ^{{\tiny {\mathsf{rbk}}}}\textsf {Seller}\).
Retractable compliance can be axiomatised in terms of derivability in a formal system whose statements do not mention histories.
Definition 9
(Formal System \(\vartriangleright \) for Retractable Compliance).

Let us formally show that \(\emptyset \vartriangleright \textsf {Buyer}\dashv ^{{\tiny {\prec }}}\textsf {Seller}\)

The formal system \(\vartriangleright \) completely axiomatises retractable compliance:
Theorem 1
(Soundness and Completeness of system \(\vartriangleright \) w.r.t \(\dashv ^{{\tiny {\mathsf{rbk}}}}\) ).
Equivalence of \(\dashv ^{{\tiny {\mathsf{A}}}}\) and \(\dashv ^{{\tiny {\mathsf{rbk}}}}\). As previously observed, the judgements of system \(\vartriangleright \) abstract away from histories, which are essential in the definition of rollback. This is possible because rollback is just a backtracking mechanism, which is however limited to the exploration of alternative branches of the reduction tree of a system rooted at retractable communications. Since affectible and retractable communications are the same, it is natural to look at system \(\vartriangleright \) to establish the equivalence among \(\dashv ^{{\tiny {\mathsf{A}}}}\) and \(\dashv ^{{\tiny {\mathsf{rbk}}}}\).
Lemma 2
If \({\rho } \dashv ^{{\tiny {\mathsf{A}}}}{\sigma }\), then one of the following conditions holds:
-
1.
\(\rho = \mathbf{1}\);
-
2.
\(\rho = \sum _{i\in I}\alpha _i.\rho _i\), \(\sigma = \sum _{j\in J}\overline{\alpha }_j.\sigma _j\) and \(\exists h \in I \cap J.\; {\rho _h} \dashv ^{{\tiny {\mathsf{A}}}}{\sigma _h}\);
-
3.
\(\rho = \bigoplus _{i\in I}\overline{a}_i.\rho _i\), \(\sigma = \sum _{j\in J}a_j.\sigma _j\), \(I\subseteq J\) and \(\forall h \in I. \; {\rho _h} \dashv ^{{\tiny {\mathsf{A}}}}{\sigma _h}\);
-
4.
\(\rho = \sum _{i\in I}a_i.\rho _i\), \(\sigma = \bigoplus _{j\in J}\overline{a}_j.\sigma _j\), \(I\supseteq J\) and \(\forall h \in J. \; {\rho _h} \dashv ^{{\tiny {\mathsf{A}}}}{\sigma _h}\).
In Theorem 1, soundness and completeness of system \(\vartriangleright \) has been proved when the symbol \(\dashv ^{{\tiny {\prec }}}\) is interpreted as the retractable compliance relation \(\dashv ^{{\tiny {\mathsf{rbk}}}}\). We now show that system \(\vartriangleright \) is sound and complete also when the symbol \(\dashv ^{{\tiny {\prec }}}\) is interpreted as the affectible compliance relation \(\dashv ^{{\tiny {\mathsf{A}}}}\). The equivalence of the relations \(\dashv ^{{\tiny {\mathsf{rbk}}}}\) and \(\dashv ^{{\tiny {\mathsf{A}}}}\) follows then as an immediate corollary.
Definition 10
(A \(\dashv ^{{\tiny {\mathsf{A}}}}\) -semantics for system \(\vartriangleright \) ). Let \(\varGamma \) be a set of statements of the form \(\rho \dashv ^{{\tiny {\prec }}}\sigma \). We define
-
(i)
\( \begin{array}{rcl} \models ^{{\tiny \mathsf{A}}}\varGamma&~~ \text{ if } ~~&\forall {(\rho ' \dashv ^{{\tiny {\prec }}}\sigma ') \in \varGamma }. \end{array}\) \( ~[\, \rho ' \dashv ^{{\tiny {\mathsf{A}}}}\sigma '\,]\);
-
(ii)
\( \begin{array}{rcl} \varGamma \models ^{{\tiny \mathsf{A}}}\rho \dashv ^{{\tiny {\prec }}}\sigma&~~ \text{ if } ~~&\models ^{{\tiny \mathsf{A}}}\varGamma ~\Rightarrow ~\rho \dashv ^{{\tiny {\mathsf{A}}}}\sigma \end{array} \).
The proof of the following Lemma is inspired to [7].
Lemma 3
(Soundness of \(\vartriangleright \) w.r.t \(\dashv ^{{\tiny {\mathsf{A}}}}\) ). If \(\varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma \), then \(\varGamma \models ^{{\tiny \mathsf{A}}}\rho \dashv ^{{\tiny {\prec }}}\sigma \).
We write \(\mathcal{D} \ {:}{:} \ \varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma \) when \(\mathcal{D}\) is a derivation in the system \(\vartriangleright \) with conclusion \(\varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma \). We can easily implement a backward proof search (from conclusion to premises) in the formal system \(\vartriangleright \) by means of a procedure \(\mathbf{Prove }\).
Lemma 4
-
(i)
Prove \((\varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma )=\mathcal{D}\ne \) fail implies \(\mathcal{D}\ {:}{:} \ \varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma \);
-
(ii)
Prove \((\varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma )\) terminates for all judgments \(\varGamma \vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma \).
Lemma 5
(Completeness of \(\vartriangleright \) w.r.t \(\dashv ^{{\tiny {\mathsf{A}}}}\) ). If \(\rho \dashv ^{{\tiny {\mathsf{A}}}}\sigma \), then \(\vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma .\)
Proof
(Sketch). If \(\rho \dashv ^{{\tiny {\mathsf{A}}}}\sigma \) then by Lemma 2 there are four possibilities; disregarding the contexts \(\varGamma \)’s, we see that each of these cases corresponds exactly to one rule in system \(\vartriangleright \), where \(\mathbf{Prove }\) is recursively applied to the respective premises, but for rule (\({\textsc {Hyp}}\)), that corresponds to an exit clause in \(\mathbf{Prove }\). It follows that \(\mathbf{Prove }(\vartriangleright \rho \dashv ^{{\tiny {\prec }}}\sigma )\ne \mathbf fail \), so that the thesis follows by Lemma 4, since \(\mathbf{Prove }\) always terminates either returning a correct derivation or \(\mathbf{fail }\).
Corollary 1
\( \dashv ^{{\tiny {\mathsf{rbk}}}}~~ = ~~ \dashv ^{{\tiny {\mathsf{A}}}}\)
Proof
2 Game-Theoretic Interpretation of Retractable Contracts
Following [5] we interpret affectible contracts as certain games over event structures. This yields a game-theoretic interpretation of affectible contracts, and hence of retractable contracts by Corollary 1. For the reader’s convenience we briefly recall the basic notions of event structure and game associated to an LTS.
Definition 11
(Event structure [15]). Let \(\mathbf E\) be a denumerable universe of events and let \(\mathbf A\) be a universe of action labels. Besides, let \(\#\subseteq E\times E\) be an irreflexive and symmetric relation (called conflict relation).
-
(i)
The predicate CF on sets \(X\subseteq E\) and the set Con of finite conflict-free sets are defined by CF \((X)=\forall e,e'\in X. \lnot (e\#e')\) Con = \(\{\,X\subseteq _{\textit{fin}} E \mid \text{ CF }(X)\,\}\)
-
(ii)
An event structure is a quadruple \(\mathcal {E} = (E,\#,\vdash , l)\) where
-
\(\vdash \,\subseteq {Con}\times E\) is a relation such that \(sat(\vdash )=\;\vdash \) (i.e. \(\vdash \) is saturated), where \( sat(\vdash )=\,\{\,(Y,e)\mid X\vdash e \& X\subseteq Y\in {Con}\,\}\);
-
\(\text{ l }: E\rightarrow \mathbf A\) is a labelling function.
-
Given a set E of events, \(E^\infty \) denotes the set of sequences (both finite and infinite) of its elements. We denote by \(\varvec{e} = \langle e_0 e_1\cdots \rangle \) a sequence of eventsFootnote 1. Given \(\varvec{e}\), we denote by \(\widehat{\varvec{e}}\) the set of its elements, by \(|\varvec{e}|\) its length (either a natural number or \(\infty \)) and by \(\varvec{e}_{\!/ i}\) for \(i < |\varvec{e}|\) the subsequence \(\langle e_0e_1\cdots e_{i-1}\rangle \) of its first i elements. Given a set X we denote by |X| its cardinality. \(\mathbb {N}\) is the set of natural numbers.
Definition 12
(LTS over configurations [5]). Given an event structure \(\mathcal {E}= (E,\#,\vdash , \text{ l })\), we define the LTS \(({\mathcal {P}_{\!{fin}}(E)},E,\rightarrow _\mathcal {E})\) as follows:
Given an LTS \((S,\rightarrow )\) and a state \(s\in S\), we denote by \((s, \rightarrow )\) the restriction of \(\rightarrow \) to the transitions starting with the state s, and by \(\mathsf{T\!r}(s,\rightarrow )\) the set of the (finite or infinite) traces in \((s, \rightarrow )\) out of s.
Multi-player Games. All the subsequent definitions and terminology are from [5], except in the case of games that we call multi-player instead of “contracts”, which would be confusing in the present setting.
A set of participants (players) to a game will be denoted by \(\mathfrak {P}\), whereas the universe of partecipants is denoted by \(\mathfrak {P}_\mathfrak {U}\). We shall use A, B,...as variables ranging over \(\mathfrak {P}\) or \(\mathfrak {P}_\mathfrak {U}\). The symbols \(\mathsf A\), \(\mathsf B\), ...will denote particular elements of \(\mathfrak {P}\) or \(\mathfrak {P}_\mathfrak {U}\). We assume that each event is associated to a player by means of a function \(\pi : \mathbf {E} \rightarrow \mathfrak {P}_\mathfrak {U}\). Moreover, given \(A\in \mathfrak {P}_\mathfrak {U}\) we define \(\mathbf {E}_A =\{\,e\in \mathbf {E} \mid \pi (e)= A\,\}\).
Definition 13
(Multi-player game).
-
(i)
A game \(\mathcal {G}\) is a pair \((\mathcal {E},\varPhi )\) where \(\mathcal {E}= (E,\#,\vdash , \text{ l })\) is an event structure and \(\varPhi : \mathfrak {P}_\mathfrak {U}\rightharpoonup E^\infty \rightarrow \{\,-1,0,1\,\}\) associates each participant and trace with a payoff. Moreover, for all \(X\vdash e\) in \(\mathcal {E}\), \(\varPhi (\pi (e))\) is defined. We say that \(\mathcal {G}\) is a game with partecipants \(\mathfrak {P}\) whenever \(\varPhi A\) is defined for any player A in \(\mathfrak {P}\).
-
(ii)
A play of a game \(\mathcal {G}=(\mathcal {E},\varPhi )\) is a (finite or infinite) trace of \((\emptyset ,\rightarrow _\mathcal {E})\) i.e. an element of \(\mathsf{T\!r}(\emptyset ,\rightarrow _\mathcal {E})\).
Definition 14
(Strategy and conformance). A strategy \(\varSigma \) for a participant A in a game \(\mathcal {G}\) is a function which maps each finite play \(\varvec{e}=\langle e_0\cdots e_n\rangle \) to a (possibly empty) subset of \(\mathbf {E}_A\) such that: \(e\in \varSigma (\varvec{e}) ~\Rightarrow ~\varvec{e}e { \ is \ a \ play \ of \ } \mathcal {G}.\)
A play \(\varvec{e}=\langle e_0e_1\cdots \rangle \) conforms to a strategy \(\varSigma \) for a partecipant A in \(\mathcal {G}\) if, for all \(i\ge 0\), \( e_i\in \mathbf {E}_A ~\Rightarrow ~e_i\in \varSigma (\varvec{e}_{\!/ i}).\)
Although events, namely moves, are associated to players via the map \(\pi \), this is not injective in general, so that players can share moves. In general there are neither a turn rule nor alternation of players, similarly to concurrent games in [1]. A strategy \(\varSigma \) provides “suggestions” to some player on how to legally move continuing finite plays (also called “positions” in game-theoretic literature). But \(\varSigma \) may be ambiguous at some places, since \(\varSigma (\varvec{e})\) may contain more than an event; in fact it can be viewed as a partial mapping which is undefined when \(\varSigma (\varvec{e}) = \emptyset \).
We refer to [5] for the general definition of winning strategy for multi-player games (briefly recalled also in Remark 1 below), since it involves the conditions of fairness and innocence, which will be trivially satisfied in our interpretation of affectible client/server systems, where the notion of winning strategy corresponds to the one given in Definition 19.
Turn-Based Operational Semantics and Compliance. Toward the game theoretic interpretation of a client/server system \(\rho \,\Vert \,\sigma \), we introduce a slightly different description of the semantics of affectible contracts, making explicit the idea of a three-player game. We interpret the internal choices and the input actions of the client as moves of a player \(\mathsf A\) and the internal choices and the input actions of the server as moves of a player \(\mathsf B\). The synchronisations due to affectible choices are instead interpreted as moves of the third player \(\mathsf C\).
From a technical point of view this is a slight generalization and adaptation to our scenario of the turn-based semantics of “session types” in [5], Sect. 5.2. The changes are needed both because we have three players instead of two, and because session types are just session contracts, that is affectible contracts without affectible outputs.
Definition 15
(Single-buffered \(\mathsf {A\!S\!C}\) ). The set \(\mathsf {A\!S\!C}^{[\,]}\) of single-buffered affectible contracts is defined by \(\mathsf {A\!S\!C}^{[\,]}= \mathsf {A\!S\!C}\cup \{\,\mathbf{0}\,\}\cup \{\,[\overline{a}_k]\sigma _k \mid \oplus _{i\in I} \overline{a}_i.\sigma _i \in \mathsf {A\!S\!C}, k\in I\,\}\)
We use the symbols \(\tilde{\rho }, \tilde{\sigma },\tilde{\rho }',\tilde{\sigma }'\ldots \) to denote elements of \(\mathsf {A\!S\!C}^{[\,]}\). A turn-based configuration (configuration for short) is a pair \(\tilde{\rho } \,\mid \mid \mid \,\tilde{\sigma }\), where \(\tilde{\rho },\tilde{\sigma }\in \mathsf {A\!S\!C}^{[\,]}\).
As in [5], we have added the “single buffered” contracts \([\overline{a}]\sigma \) to represent the situation in which \(\overline{a}\) is the only output offered after an internal choice. Since the actual synchronization takes place in a subsequent step, \(\overline{a}\) is “buffered” in front of the continuation \(\sigma \).
Definition 16
(Turn-based operational semantics of configurations). Let  . In Fig. 1 we define the LTS \(\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\,}}\) over turn-based configurations, with labels in \(\mathbf{{tbAct}}\).
. In Fig. 1 we define the LTS \(\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\,}}\) over turn-based configurations, with labels in \(\mathbf{{tbAct}}\).
Comparing \(\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\,}}\) with the LTS for affectible contracts, we observe that \([\overline{a}]\sigma \) is a duplicate of \(\overline{a}.\sigma \), with the only difference that now there is a redundant step in \(\oplus _{i\in I}\overline{a}_i.\rho _i\,\mid \mid \mid \,\tilde{\sigma }\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\mathsf A:\overline{a}_k\,}}[\overline{a}_k]\rho _k \,\mid \mid \mid \,\tilde{\sigma }\) when I is the singleton \(\{\,k\,\}\). Also we have the new reduction  to signal when player \(\mathsf C\) wins.
to signal when player \(\mathsf C\) wins.
Let \(\varvec{\beta }\!=\!\langle \beta _1\cdots \beta _n\rangle \!\in \!\mathbf{{tbAct}}^*\). We shall use the notation \(\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\varvec{\beta }\,}}=\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\beta _1\,}}\!\!\circ \cdots \circ \!\!\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\beta _n\,}}\)
Definition 17
(Turn-Based Compliance Relation \(\dashv ^{{\tiny \mathsf{t\!b}}}\) ).
-
(i)
Let \(\mathcal{H}: \mathcal{P}(\mathsf {A\!S\!C}^{[\,]}\times \mathsf {A\!S\!C}^{[\,]})\rightarrow \mathcal{P}(\mathsf {A\!S\!C}^{[\,]}\times \mathsf {A\!S\!C}^{[\,]})\) be such that, for any
 , we get
, we get  if:
if:-
(1)
\(\tilde{\rho }\,\mid \mid \mid \,\tilde{\sigma }~\not \!\!\!\!\!\!\!\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\,}}\) implies \(\rho =\mathbf{0}\);
-
(2)
\(\forall \tilde{\rho }',\tilde{\sigma }' \). \( [~ \tilde{\rho }\,\mid \mid \mid \,\tilde{\sigma }\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\beta \,}} {\tilde{\rho }'}\,\mid \mid \mid \,{\tilde{\sigma }'}\) implies
 , where \(\beta \in \{\mathsf A{:}a,\mathsf A{:}\overline{a},\mathsf B{:}a,\mathsf B{:}\overline{a} \mid a\in \mathcal{N}\}\);
, where \(\beta \in \{\mathsf A{:}a,\mathsf A{:}\overline{a},\mathsf B{:}a,\mathsf B{:}\overline{a} \mid a\in \mathcal{N}\}\); -
(3)
\(\exists a\in \mathcal{N}. \tilde{\rho }\,\mid \mid \mid \,\tilde{\sigma }\!\!\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\mathsf C:a\,}}\) implies \(\exists \tilde{\rho }',\tilde{\sigma }',a \). \([\tilde{\rho }\,\mid \mid \mid \,\tilde{\sigma }\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\mathsf C:a\,}} {\tilde{\rho }'}\,\mid \mid \mid \,{\tilde{\sigma }'}\) and
 ;
;
-
(1)
-
(ii)
A relation
 is a turn-based compliance relation if
is a turn-based compliance relation if  . \(\dashv ^{{\tiny \mathsf{t\!b}}}\) is the greatest solution of the equation \(X=\mathcal{H}(X)\), that is \(\dashv ^{{\tiny \mathsf{t\!b}}}~=~\nu \mathcal{H}\).
. \(\dashv ^{{\tiny \mathsf{t\!b}}}\) is the greatest solution of the equation \(X=\mathcal{H}(X)\), that is \(\dashv ^{{\tiny \mathsf{t\!b}}}~=~\nu \mathcal{H}\). -
(iii)
For \(\rho ,\sigma \in \mathsf {A\!S\!C}\), we say that \(\rho \) is turn-based compliant with \(\sigma \) if \(\rho \dashv ^{{\tiny \mathsf{t\!b}}}\sigma \).
Turn-based compliance is equivalent to affectible compliance
Theorem 2
Let \(\rho ,\sigma \in \mathsf {A\!S\!C}\). \( \rho \dashv ^{{\tiny \mathsf{t\!b}}}\sigma ~~~~ \Leftrightarrow ~~~~ \rho \dashv ^{{\tiny {\mathsf{A}}}}\sigma .\)
Three-Player Game Interpretation for ASC Client/Server Systems. Using the turn-based semantics, we associate to any client/server system an event structure, and then a three-player gameFootnote 2, extending the treatment of session types with two-player games in [5]. For our purposes we just consider the LTS of a given client/server system instead of an arbitrary one.
Definition 18
(ES of affectible-contracts systems). Let \(\rho \,\Vert \,\sigma \) be a client/server system of affectible contracts. We define the event structure \([\![ \rho \,\Vert \,\sigma ]\!]=(E,\#,\vdash , \text{ l })\), where
-
\(E=\{\,(n,\beta ) \mid n\in \mathbb {N}, \beta \in \mathbf{{tbAct}}\,\}\)
-
\(\# = \{\,((n,\beta _1),(n,\beta _2)) \mid n\in \mathbb {N}, \beta _1,\beta _2 \in \mathbf{{tbAct}}, \beta _1\ne \beta _2\,\}\)
-
\(\vdash \, =\, sat{\vdash _{\!\rho \!\,\Vert \,\!\sigma }}\) where \(\vdash _{\!\rho \!\,\Vert \,\!\sigma } = \{\,(X,(n,\beta )) \mid \rho \,\mid \mid \mid \,\sigma \mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\textit{snd}(X)\,}} \tilde{\rho }'\,\mid \mid \mid \,\tilde{\sigma }' \!\!\mathrel {\mathop {~\longrightarrow ~}\limits ^{\,\beta \,}} { \ and \ } n=|X|+1\,\}\)
-
\(\text{ l }(n,\beta ) = \beta \).
where the partial function \(\textit{snd}(\text{- })\) maps any \(X= \{\,(i,\beta _i)\,\}_{i=1..n}\) to \(\langle \beta _1\cdots \beta _n\rangle \), and it is undefined over sets not of the shape of X.
Events in \([\![ \rho \,\Vert \,\sigma ]\!]\) are actions in \(\mathbf{{tbAct}}\) paired with time stamps. Two events are in conflict if different actions should be performed at the same time, so that configurations must be linearly ordered w.r.t. time. The relation \(X \vdash _{\!\rho \!\,\Vert \,\!\sigma } (n,\beta )\) holds if X is a trace in the LTS of \(\rho \,\Vert \,\sigma \) of length \(n-1\); therefore the enabling \(Y \vdash (n,\beta )\) holds if and only if Y includes a trace of length \(n-1\) that can be prolonged by \(\beta \), possibly including \((n,\beta )\) itself and any other action that might occur after \(\beta \) in the LTS.
So, by the above, \(\vdash _{\mathsf {Buyer}\!\,\Vert \,\!\mathsf {Seller}}\) in \([\![ \mathsf {Buyer}\,\Vert \,\mathsf {Seller} ]\!]\) corresponds to

The \(\vdash _{\!\rho \!\,\Vert \,\!\sigma }\) of this simple example is finite. It is not so in general for systems with recursive contracts.
The following definition is a specialisation of Definitions 4.6 and 4.7 in [5]. We use \(\mathsf{M\!\,a\!\,x\!T\!r}(s,\rightarrow )\) and \(\mathsf{F\!\,i\!\,n\!\,M\!\,a\!\,x\!T\!r}(s,\rightarrow )\) to denote the set of maximal traces and finite maximal traces, respectively, of \(\mathsf{T\!r}(s,\rightarrow )\).
Definition 19
Given \(\rho ,\sigma \in \mathsf {A\!S\!C}\), we define the game \(\mathcal {G}_{\rho \!\,\Vert \,\!\sigma }\) as \(([\![ \rho \,\Vert \,\sigma ]\!],\varPhi )\), where \(\pi (n,\beta ) = A\) if \(\beta = A{:}\alpha \), \(\varPhi A\) is defined only if \(A\in \{\,\mathsf A,\mathsf B,\mathsf C\,\}\) and
where \(\mathbf {P}(A,\varvec{e})\) holds whenever

A player A wins in the sequence of events \(\varvec{e}\) if \(\varPhi A\,\varvec{e} > 0\). A strategy \(\varSigma \) for player A is winning if A wins in all plays conforming to \(\varSigma \).
Note that, \(\mathbf {P}(A,\varvec{e})\) holds for any A and infinite element \(\varvec{e}\) of \(\mathsf{T\!r}(\emptyset ,\rightarrow _{[\![ \rho \!\,\Vert \,\!\sigma ]\!]})\).
For the game \(\mathcal {G}_{\mathsf {Buyer}\,\Vert \,\mathsf {Seller}}\), it is possible to check that, for instance,
where \(\varvec{s_1} \!=\)  ,
,
\(\varvec{s_2} =\) \((4,(\mathsf A{:}\mathtt{bag}))(1,(\mathsf C{:}\overline{\mathtt{price}}))\)
\(\varvec{s_3} =\) \((1,(\mathsf C{:}\mathtt{bag}))(2,(\mathsf B{:}\overline{\mathtt{price}}))(3,(\mathsf A{:}\mathtt{price})) (4,(\mathsf A{:}\overline{\mathtt{cash}}))(5,(\mathsf B{:}\mathtt{cash}))\)
Let us define a particular strategy \(\widetilde{\varSigma }\) for \(\mathsf C\) in \(\mathcal {G}_{\mathsf {Buyer}\,\Vert \,\mathsf {Seller}}\) as follows:

The strategy \(\widetilde{\varSigma }\) for \(\mathsf C\) in \(\mathcal {G}_{\mathsf {Buyer}\,\Vert \,\mathsf {Seller}}\) is winning.
Remark 1
According to [5], A wins in a play if \(\mathcal {W}\!A \varvec{e} > 0\), where \(\mathcal {W}\!A \varvec{e} = \varPhi A \varvec{e}\) if all players are “innocent” in \(\varvec{e}\), while if A is “culpable”, \(\mathcal {W}\!A \varvec{e} = -1\), and if A is innocent and someone else culpable, \(\mathcal {W}\!A \varvec{e}= +1\). A strategy \(\varSigma \) of A is winning if A wins in all fair plays conforming to \(\varSigma \). A play \(\varvec{e}\) is “fair” for a strategy \(\varSigma \) of a player A if any event in \(E_A\) which is infinitely often enabled is eventually performed. Symmetrically A is “innocent” in \(\varvec{e}\) if she eventually plays all persistently enabled moves of her in \(\varvec{e}\), namely if she is fair to the other players, since the lack of a move by A might obstacle the moves by others; she is “culpable” otherwise. As said above, Definition 19 is a particularisation of the general definitions in [5]. In fact in a game \(\mathcal {G}_{\rho \!\,\Vert \,\!\sigma }\) no move of any player can occur more than once in a play \(\varvec{e}\) because of time stamps. Therefore no move can be “persistently enabled”, nor it can be prevented since it can be enabled with a given time stamp only if there exists a legal transition in the LTS with the same label. Hence any player is innocent in a play \(\varvec{e}\) of \(\mathcal {G}_{\rho \!\,\Vert \,\!\sigma }\) and all plays are fair. Therefore \(\mathcal {W}\!\) coincides with \(\varPhi \).
It is possible to characterize affectible and retractable compliance in terms of the existence of a winning strategy for \(\mathsf C\) in \(\mathcal {G}_{\rho \!\,\Vert \,\!\sigma }\).
Theorem 3
\(\rho \dashv ^{{\tiny {\mathsf{A}}}}\sigma \) (or, equivalently, \(\rho \dashv ^{{\tiny {\mathsf{rbk}}}}\sigma \)) if and only if player \(\mathsf C\) has a winning strategy in the three-player game \(\mathcal {G}_{\rho \!\,\Vert \,\!\sigma }\).
3 Strategies as Orchestrators
In the present section we show that a client \(\rho \) is retractable-compliant with a server \(\sigma \) if and only if their interactions can be led to a successful state by means of the mediation of an orchestrator. To do that we show how an orchestrator can be obtained out of a “univocal” winning strategy (see Definition 24 below) for player \(\mathsf C\) in the game \(\mathcal {G}_{\rho \!\,\Vert \,\!\sigma }\), and vice versa. For a detailed discussion on orchestrators for contracts and orchestrators for session-contracts, we refer to [13, 14] and [2] respectively. In the present setting, our orchestrators, that we dub strategy-orchestrators, are defined as a variant of the session-orchestrators of [2], which in turn are a restriction of orchestrators in [14]. The task of a strategy orchestrator is to mediate the interactions between two affectible session contracts by selecting one of the possible affectible choices and constraining non-affectible ones.
We consider two sorts of orchestration actions, having the following shapes:
\(\langle {\small \alpha },{\small \overline{\alpha }}\rangle \), enabling the unaffectible synchronization \(\rho \,\Vert \,\sigma \mathrel {\xrightarrow {\,\tau \,}{}}\rho '\,\Vert \,\sigma '\);
\(\langle {\small \alpha },{\small \overline{\alpha }}\rangle ^+\), enabling the affectible synchronization \(\rho \,\Vert \,\sigma \mathrel {\xrightarrow {\,+\,}{}}\rho '\,\Vert \,\sigma '\).
Definition 20
(Strategy Orchestrators).
-
(i)
The set \(\mathbf{OrchAct }\) of strategy-orchestration actions is defined by
$$\begin{aligned} \mathbf{OrchAct }= \{\,\langle {\small \alpha },{\small \overline{\alpha }}\rangle \mid \alpha \in \mathcal{N}\cup \overline{\mathcal{N}}\,\}\cup \{\,\langle {\small \alpha },{\small \overline{\alpha }}\rangle ^+ \mid \alpha \in \mathcal{N}\cup \overline{\mathcal{N}}\,\} \end{aligned}$$We let \(\mu ,\mu ',\ldots \) range over elements of \(\mathbf{OrchAct }\) with the shape \(\langle {\small \alpha },{\small \overline{\alpha }}\rangle \), and \(\mu ^+,{\mu '}^+,\ldots \) range over elements of \(\mathbf{OrchAct }\) with the shape \(\langle {\small \alpha },{\small \overline{\alpha }}\rangle ^+\).
-
(ii)
We define the set \(\text{ Orch }\) of strategy orchestrators, ranged over by \(f, g, \ldots \), as the closed (with respect to the binder \(\mathsf{rec} \, \)) terms generated by the following grammar:
$$ \begin{array}{lrl@{}l@{}l} f, g &{} \ {:}{:=} \ &{} \mathfrak {1}&{} {idle}\\ &{} \mid &{} \mu ^+.f &{} {\textit{prefix}} \\ &{} \mid &{} \mu _1.f_1\vee \ldots \vee \mu _n.f_n &{} {disjunction}\\ &{} \mid &{} x &{} {variable}\\ &{} \mid &{} \mathsf{rec} \, x.f &{} {recursion} \end{array} $$where the \(\mu _i\) in a disjunction are pairwise distinct. Moreover, we impose strategy orchestrators to be contractive, i.e. the f in \(\mathsf{rec} \, x.f\) is assumed not to be a variable.
We write \(\bigvee _{i\in I}\mu _i.f_i\) as short for \(\mu _1.f_1\vee \ldots \vee \mu _n.f_n\), where \(I=\{\,1,\ldots , n\,\}\).
If not stated otherwise, we consider recursive orchestrators up-to unfolding, that is we equate \(\mathsf{rec} \, x .f \) with \(f\{x/\mathsf{rec} \, x .f\}\). We omit trailing \(\mathfrak {1}\)’s.
Strategy orchestrators are “simple orchestrators” in [14] and “synchronous orchestrators” in [13], but for the kind of prefixes which are allowed in a single prefix or in a disjunction. In fact a prefix \(\langle {\small \alpha },{\small \overline{\alpha }}\rangle ^+\) cannot occur in disjunctions, where all the orchestrators must be prefixed by \(\langle {\small \alpha },{\small \overline{\alpha }}\rangle \) actions.
Definition 21
(Strategy orchestrators LTS). We define the labelled transition system (Orch, OrchAct, \(\mathop {\mapsto }\limits ^{})\) by
An orchestrated system, represented by \(\rho \mathbin {\Vert _{f}} \sigma \), is client/server system whose interaction is mediated by an orchestrator.
Definition 22
(LTS for orchestrated-systems). Let \(\rho ,\sigma \in \mathsf {A\!S\!C}\) and \(f\in \) Orch.

Moreover, we define \(\mathrel {\mathop {\Longrightarrow }\limits ^{}} \,=\, \mathrel {\xrightarrow {\,\,}{\!\!^*}}\circ \, (\mathrel {\xrightarrow {\,\tau \,}{}}\cup \mathrel {\xrightarrow {\,+\,}{}})\).
In both transitions \(\mathrel {\xrightarrow {\,+\,}{}}\) and \(\mathrel {\xrightarrow {\,\tau \,}{}}\) synchronization may happen only if the orchestrator has a transition with the appropriate pair of actions. This is because in an orchestrated interaction both client and server are committed to the synchronizations allowed by the orchestrator only. It is then clear that an orchestrator always selects one synchronisation of affectible actions on client and server side, while the disjunction of orchestrators represents the constraint that only certain synchronisations of unaffectible actions are permitted.
Definition 23
(Strategy-orchestrated Compliance).
-
(i)
\(f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \) if for any \(\rho '\) and \(\sigma '\), the following holds:
$$ \begin{array}{rcl} \rho \mathbin {\Vert _{f}} \sigma \mathrel {\mathop {\Longrightarrow }\limits ^{}}^* \rho ' \mathbin {\Vert _{f'}} \sigma ' ~\not \!\!\mathrel {\mathop {\Longrightarrow }\limits ^{}}&~~{ \ implies \ }~~&\rho '=\mathbf{1}. \end{array} $$ -
(ii)
\( \begin{array}{@{}rcl} \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma&~~\text {if}~~&\exists f .~~[\, f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \,]. \end{array} \)
Definition 24
(Univocal strategies). \(\varSigma \) is univocal if \(\forall \varvec{e}.~|\varSigma (\varvec{e})| \le 1\).
The strategy \(\widetilde{\varSigma }\) for \(\mathsf C\) in \(\mathcal {G}_{\mathsf {Buyer}\,\Vert \,\mathsf {Seller}}\), defined in the previous section, is univocal.
The proof of the following theorem relies on the fact that any orchestrator f such that \(f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \) corresponds to a univocal winning strategies for player \(\mathsf C\) in \(\mathcal {G}_{\rho \,\Vert \,\sigma }\). Vice versa a univocal winning strategy \(\varSigma \) for \(\mathsf C\) always induces an orchestrator \(f_\varSigma \). It is not restrictive to look at univocal strategies only, as established in the next lemma.
We say that \(\varSigma \) refines \(\varSigma '\), written \(\varSigma \le \varSigma '\), if and only if \(\varSigma (\varvec{e}) \subseteq \varSigma '(\varvec{e})\) for all \(\varvec{e}\).
Lemma 6
If \(\mathsf C\) has a winning strategy \(\varSigma \), then \(\mathsf C\) has a univocal winning strategy \(\varSigma '\) such that \(\varSigma '\le \varSigma \).
Theorem 4
\(\exists f .~~[\, f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \,] {~~\Leftrightarrow ~~}\text{ there } \text{ exists } \text{ a } \text{ winning } \text{ strategy } \text{ for } \text{ player } \mathsf C \text{ in } \mathcal {G}_{\rho \,\Vert \,\sigma }.\)
In particular, a winning strategy for player \(\mathsf C\) in \(\mathcal {G}_{\rho \,\Vert \,\sigma }\) can be obtained out of an orchestrator f such that \(f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \), and vice versa.
The orchestrator that can be obtained out of the strategy \(\widetilde{\varSigma }\) is
Remark 2
Univocal strategies correspond to strategy-orchestrators and are technically easier to work with. On the other hand, we can recover a full correspondence among \(\mathsf C\) strategies and orchestrators by allowing disjunctions of affectible synchronization actions \(\langle {\small \alpha },{\small \overline{\alpha }}\rangle ^+\). In a session-based scenario, however, we expect any nondeterminism to depend solely on either the client or the server. By allowing \(f=\langle {\small \overline{a}},{\small a}\rangle ^+.f_1\vee \langle {\small \overline{b}},{\small b}\rangle ^+.f_2\) in the system \({a.\rho _1 + b.\rho _2 \mathbin {\Vert _{f}} \overline{a}.\sigma _1 + \overline{b}.\sigma _2}\), the nondeterminism would depend on the orchestrator too.
Based on the formal system of Definition 9, the algorithm \(\mathbf{Synth }\) in Fig. 2 takes a (initially empty) set of assumptions \(\varGamma \), and the affectible contracts \(\rho \) and \(\sigma \), and it returns a set O of orchestrators (and hence a set of strategies by the above) if any, such that for any \(f\in O\) we have \(f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \); the algorithm returns the empty set otherwise. In the algorithm \(\mathbf{Synth }\) we consider orchestrators as explicit terms, that is we do not consider recursion up-to unfolding.
Theorem 5
(Soundness and Completeness of Synth ). The algorithm Synth is correct and complete in the following sense:
-
(i)
Synth \((\varGamma , \rho , \sigma )\) terminates for any \(\varGamma ,\rho \) and \(\sigma \).
-
(ii)
If \(f\in \) Synth \((\emptyset , \rho , \sigma )\ne \emptyset \) then \(f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \).
-
(iii)
If \(f: \rho \dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\sigma \) then there exists \(g\in \) Synth \((\emptyset , \rho , \sigma )\ne \emptyset \) such that the (possibly infinite) unfolding of f and g yields the same regular tree.
It is not difficult to check that by computing Synth \((\emptyset , \mathsf {Buyer},\mathsf {Seller})\) we get a set just consisting of the orchestrator corresponding to the strategy \(\widetilde{\varSigma }\), namely

Using the previous results and Lemma 6 we get the following:
Corollary 2
-
(i)
The relation \(\dashv \!\!\!\dashv ^{{\tiny \mathsf{Orch}}}\) is decidable.
-
(ii)
For any \(\rho ,\sigma \in \mathsf {A\!S\!C}\), it is decidable whether there exists a winning strategy for player \(\mathsf C\) in \(\mathcal {G}_{\rho \,\Vert \,\sigma }\).
Moreover, in case a winning strategy exists, it is possible to effectively compute a univocal winning strategy.
4 Conclusion and Future Work
We have studied two approaches to loosening compliance among a client and a server in contract theory, based on the concepts of dynamic adaptation and of mediated interaction respectively. We have seen that these induce equivalent notions of compliance, which can be shown via the abstract concept of winning strategy in a suitable class of games.
The byproduct is that the existence of the agreement among two contracts specifying adaptive behaviours is established by statically synthesizing the proper orchestrator, hence avoiding any trial and error mechanism at run time. The study in this paper has been limited to the case of binary sessions since this is the setting in which both orchestrators and retractable contracts have been introduced. However strategy based concepts of agreement have been developed in the more general scenario of multiparty interaction, which seems a natural direction for future work.
Notes
- 1.
Differently than in [5], we use the notation \(\varvec{e}\) for sequences instead of \(\sigma \), which refers to a contract here.
- 2.
References
Abramsky, S., Mellies, P.A.: Concurrent games and full completeness. In: Proceedings of the 14th Symposium on Logic in Computer Science, pp. 431–442 (1999)
Barbanera, F., van Bakel, S., de’ Liguoro, U.: Orchestrated session compliance. In: Proceedings ICE 2015. EPTCS, vol. 189, pp. 21–36 (2015)
Barbanera, F., de’ Liguoro, U.: Sub-behaviour relations for session-based client/server systems. MSCS 25(6), 1339–1381 (2015)
Barbanera, F., Dezani-Ciancaglini, M., Lanese, I., de’ Liguoro, U.: Retractable contracts. In: PLACES. EPTCS, vol. 203, pp. 61–72. Open Publishing Ass. (2015)
Bartoletti, M., Cimoli, T., Pinna, G.M., Zunino, R.: Contracts as games on event structures. J. Logical Algebraic Methods Progr. 85(3), 399–424 (2016)
Bernardi, G., Hennessy, M.: Compliance and testing preorders differ. In: Counsell, S., Núñez, M. (eds.) SEFM 2013. LNCS, vol. 8368, pp. 69–81. Springer, Heidelberg (2014)
Brandt, M., Henglein, F.: Coinductive axiomatization of recursive type equality and subtyping. Fundam. Inform. 33(4), 309–338 (1998)
Bravetti, M., Zavattaro, G.: A theory of contracts for strong service compliance. Math. Struct. Comput. Sci. 19(3), 601–638 (2009)
Castagna, G., Gesbert, N., Padovani, L.: A theory of contracts for web services. ACM Trans. Prog. Lang. Sys. 31(5), 19:1–19:61 (2009)
Gay, S., Hole, M.: Subtyping for session types in the Pi-Calculus. Acta Informatica 42(2/3), 191–225 (2005)
Laneve, C., Padovani, L.: The Must preorder revisited. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 212–225. Springer, Heidelberg (2007)
Nicola, R.D., Hennessy, M.: Testing equivalence for processes. In: Díaz, J. (ed.) ICALP 1983. LNCS, vol. 154, pp. 548–560. Springer, Heidelberg (1983)
Padovani, L.: Contract-based discovery and adaptation of web services. In: Bernardo, M., Padovani, L., Zavattaro, G. (eds.) SFM 2009. LNCS, vol. 5569, pp. 213–260. Springer, Heidelberg (2009)
Padovani, L.: Contract-based discovery of web services modulo simple orchestrators. Theoret. Comput. Sci. 411, 3328–3347 (2010)
Winskel, G.: Event structures. In: Brauer, W., Reisig, W., Rozenberg, G. (eds.) Advances in Petri Nets 1986, Part II. LNCS, vol. 255, pp. 325–392. Springer, Heidelberg (1987)
Acknowledgments
The authors wish to thank Massimo Bartoletti for an insightful discussion, Mariangiola Dezani for her everlasting support and the three anonymous referees for their help in improving the final version of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Barbanera, F., de’ Liguoro, U. (2016). A Game Interpretation of Retractable Contracts. In: Lluch Lafuente, A., Proença, J. (eds) Coordination Models and Languages. COORDINATION 2016. Lecture Notes in Computer Science(), vol 9686. Springer, Cham. https://doi.org/10.1007/978-3-319-39519-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-39519-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39518-0
Online ISBN: 978-3-319-39519-7
eBook Packages: Computer ScienceComputer Science (R0)





 , we get
, we get  if the following conditions hold:
if the following conditions hold: ;
;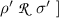 .
. is an affectible compliance relation if
is an affectible compliance relation if  .
. 
 , we get
, we get  if:
if: , where
, where  ;
; is a turn-based compliance relation if
is a turn-based compliance relation if  .
. 