Automatic Detection of Latent Common Clusters of Groups in MultiGroup Regression

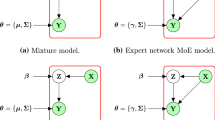
Abstract

We present a flexible non-parametric generative model for multigroup regression that detects latent common clusters of groups. The model is founded on techniques that are now considered standard in the statistical parameter estimation literature, namely, Dirichlet process(DP) and Generalized Linear Model (GLM), and therefore, we name it “Infinite MultiGroup Generalized Linear Models” (iMG-GLM). We present two versions of the core model. First, in iMG-GLM-1, we demonstrate how the use of a DP prior on the groups while modeling the response-covariate densities via GLM, allows the model to capture latent clusters of groups by noting similar densities. The model ensures different densities for different clusters of groups in the multigroup setting. Secondly, in iMG-GLM-2, we model the posterior density of a new group using the latent densities of the clusters inferred from previous groups as prior. This spares the model from needing to memorize the entire data of previous groups. The posterior inference for iMG-GLM-1 is done using Variational Inference and that for iMG-GLM-2 using a simple Metropolis Hastings Algorithm. We demonstrate iMG-GLM’s superior accuracy in comparison to well known competing methods like Generalized Linear Mixed Model (GLMM), Random Forest, Linear Regression etc. on two real world problems.