Selecting Random Effect Components in a Sparse Hierarchical Bayesian Model for Identifying Antigenic Variability

Abstract

In Foot-and-Mouth Disease Virus (FMDV), understanding how viruses offer protection against related emerging strains is vital for creating effective vaccines. With testing large numbers of vaccines being infeasible, the development of an in silico predictor of cross-protection between virus strains has been a vital area of recent research. The current paper reviews a recent contribution to this area, the SABRE method, a sparse hierarchical Bayesian model which uses spike and slab priors to identify key antigenic sites within FMDV serotypes. WAIC is then combined with the SABRE method and its ability to approximate Bayesian Cross Validation performance in terms of correctly selecting random effect components analysed. WAIC and the SABRE method have then been applied to two FMDV datasets and the results analysed.

10 Appendix

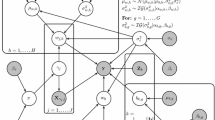
For the Gibbs sampling we sample the intercept and regression coefficients together and define $\mathbf w _{\varvec{\gamma }}^* = (w_0,\mathbf w _{\varvec{\gamma }}^\top )^\top$, $\mathbf X _{\varvec{\gamma }}^* = (\mathbf 1 ,\mathbf X _{\varvec{\gamma }})$, $\mathbf m _{\varvec{\gamma }} = (\mu _{w_0},\mu _{w,1},\ldots ,\mu _{w,1},$ $\mu _{w,2},\ldots ,\mu _{w,H})^\top$ and $\varvec{\varSigma }_\mathbf{w _{\varvec{\gamma }}^*} = diag(\varvec{\sigma }_\mathbf{w ^*}^2)$ with $\varvec{\sigma }_\mathbf{w ^*}^2 = (\sigma ^2_{w_0},\sigma ^2_{w,1},\ldots ,\sigma ^2_{w,1},\sigma ^2_{w,2},$ $\ldots ,\sigma ^2_{w,H})^\top$. Each $\mu _{w,h}$ and $\sigma _{w,h}^2$ is repeated with length $||\mathbf w _{\varvec{\gamma },h}||$ dependent on $\varvec{\gamma }$. The Gibbs sampling distributions are then given as follows, with $\varvec{\theta }'$ used to denote all the parameters not on the left of the conditioning bar:

$$\begin{aligned} \!\!\mathbf w _{\varvec{\gamma }}^* | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\mathcal {N}(\mathbf w _{\varvec{\gamma }}^* | \mathbf V _\mathbf{w _{\varvec{\gamma }}^*} \mathbf X _{\varvec{\gamma }}^{*\top } (\mathbf y - \mathbf Z {} \mathbf b ) + \mathbf V _\mathbf{w _{\varvec{\gamma }}^*} \varvec{\varSigma }_\mathbf{w _{\varvec{\gamma }}^*}^{-1}{} \mathbf m _{\varvec{\gamma }}, \sigma _\varepsilon ^2 \mathbf V _\mathbf{w _{\varvec{\gamma }}^*}) \end{aligned}$$

(12)

$$\begin{aligned} \!\!\mathbf b | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\mathcal {N}(\mathbf b | \tfrac{1}{\sigma _\varepsilon ^2}{} \mathbf V _\mathbf{b } \mathbf Z ^\top (\mathbf y - \mathbf X _{\varvec{\gamma }}^* \mathbf w _{\varvec{\gamma }}^*), \mathbf V _\mathbf{b }) \end{aligned}$$

(13)

$$\begin{aligned} \!\!\sigma _{b,g}^2 | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\mathcal {IG}(\sigma _{b,g}^2 | ~ ||\mathbf b _g||/2 + \alpha _{b,g}, \beta _{b,g} + \tfrac{1}{2} \mathbf b _g^\top \mathbf b _g)\end{aligned}$$

(14)

$$\begin{aligned} \!\!\mu _{w,h} | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\mathcal {N} (\mu _{w,h} | V_{\mu _\gamma ,h}^{-1}( {\scriptstyle \sum }(\mathbf w _{\varvec{\gamma },h})/\sigma _{w,h}^{2} + \mu _{0,h}/\sigma _{0,h}^2), \sigma _\varepsilon ^2 V_{\mu _\gamma ,h}) \end{aligned}$$

(15)

$$\begin{aligned} \!\!\sigma _{w,h}^2 | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\end{aligned}$$

(16)

$$\begin{aligned} \mathcal {IG}(\sigma _{w,h}^2 | ~ ||\mathbf w _{\varvec{\gamma },h}&||/2 + \alpha _{w,h}, \beta _{w,h} + \tfrac{1}{2 \sigma _\varepsilon ^2} (\mathbf w _{\varvec{\gamma },h} - \mathbf 1 \mu _{w,h})^\top (\mathbf w _{\varvec{\gamma },h} - \mathbf 1 \mu _{w,h})) \nonumber \\ \sigma _{\varepsilon }^2 | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\mathcal {IG}(\sigma _{\varepsilon }^2 | (N + ||\mathbf w _{\varvec{\gamma }}^*|| + H)/2 + \alpha _\varepsilon , \beta _\varepsilon + \tfrac{1}{2}R_{\sigma _\varepsilon ^2}) \end{aligned}$$

(17)

$$\begin{aligned} \pi | \varvec{\theta }', \mathbf X _{\varvec{\gamma }}^*, \mathbf Z , \mathbf y \sim&\mathcal {B}(\pi | \alpha _\pi + ||\varvec{\gamma }||, \beta _\pi + J - ||\varvec{\gamma }||) \end{aligned}$$

(18)

where we sample $\sigma _{b,g}^2$, $\mu _{w,h}$ and $\sigma _{w,h}^2$ for each g and h respectively. We also define $\mathbf V _\mathbf{w _{\varvec{\gamma }}^*} = (\mathbf X _{\varvec{\gamma }}^{*\top } \mathbf X _{\varvec{\gamma }}^* + \varvec{\varSigma }_\mathbf{w _{\varvec{\gamma }}^*}^{-1})^{-1}$, $\mathbf V _\mathbf{b } = (\tfrac{1}{\sigma _\varepsilon ^2 }{} \mathbf Z ^\top \mathbf Z + \varvec{\varSigma }_\mathbf{b }^{-1})^{-1}$, $V_{\mu _\gamma ,h} = ((||\mathbf w _{\varvec{\gamma },h}|| / \sigma _{w,h}^{2})^{-1}$ $+ (\sigma _{0,h}^2)^{-1})^{-1}$ and $R_{\sigma _\varepsilon ^2} = (\mathbf y - \mathbf X _{\varvec{\gamma }}^* \mathbf w _{\varvec{\gamma }}^* -\mathbf Z {} \mathbf b )^\top (\mathbf y - \mathbf X _{\varvec{\gamma }}^* \mathbf w _{\varvec{\gamma }}^* -\mathbf Z {} \mathbf b ) + (\mathbf w _{\varvec{\gamma }}^* - \mathbf m _{\varvec{\gamma }})^\top \varvec{\varSigma }_\mathbf{w _{\varvec{\gamma }}^*}^{-1}$ $(\mathbf w _{\varvec{\gamma }}^*$ $- \mathbf m _{\varvec{\gamma }}) + \sum _{h=1}^H (\mu _{w,h} - \mu _{0,h})^2 / \sigma _{0,h}^2$ for notational simplicity.