Keywords

1 Introduction

Hyperconnectivity is used to define the interconnectedness of people, organizations, and objects which result from different technology innovations like the Internet, mobile technology and the Internet of Things (IoT) [1]. The hyperconnectivity exists not only in the communication between people but also in the connectivity of cars [2]. In addition, to make the travel and transportation more efficient and more comfortable, the hyperconnectivity is the main driver of innovation [3].

On the other hand, the transportation system is clearly overloaded by congestion in the major cities. For example in the city center of London, the average speed of cars is 14 km/h [4] while the car’s speed in the city center of Moscow is around 6 km/h [5]. Positively, this can be an opportunity to improve interconnectedness of cars in the city environment. These cars can be parts of the communication infrastructure for the Intelligent Transportation Systems (ITS) and also offer various opportunities for gathering data about a city by continually sensing events from streets and process sensed data.

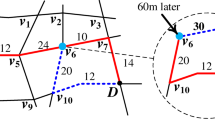
Therefore, utilizing vehicular networks as an infrastructure for urban sensing is a cost-efficient way of deploying an urban monitoring system without actually deploying connected sensors [6] (Fig. 1 shows a snapshot of the communication between moving cars within the city of Porto). Vehicles typically do not have energy constraints. Therefore, cars can be equipped with powerful wireless transmitters, processing units, and sensing devices (vibration sensors, GPS, video cameras, detectors, acoustic detectors, car sensors, etc.).

Fig. 1.
figure 1

A snapshot showing exchanged messages between taxis in the city of Porto [18]

Full size image

Thousands of cars which are networked together using wireless communication are able to connect us to a seemingly unlimited data gathered from the city environment. The gathered data can be processed and visualized live, enabling monitoring activities (Fig. 1) and better decision making. However, this data can also be serve as the basis for predictive models that can be an informative tool for the decision support systems one step further. Given the availability of the massive amount of data which is geographically distributed, data mining approaches are being used to obtain models for all parts of the city that are integrated into ITS applications [7–14].

One of the interesting examples of ITS applications is the prediction of trip duration for public transportation [15–17]. Knowing the prediction of trip duration beforehand can be very instructive for taxi companies, passengers, and drivers to make the right decision for the route planning and scheduling by using the data collected about the taxi’s trips by each taxi. Figure 1 shows a snapshot of exchanged messages between taxis in the city of Porto.

Machine learning algorithms by using the data collected by taxis relate the trip duration to several data features which describe the trip like the time of the trip, origin, destination, the weather, and the week’s day. The prediction of duration of the trip may vary from one taxi to another, due to differences in the taxi usage, the brand of the vehicle, the driving habits, and the route.

In addition, taking advantage of the massive amount of gathered data, the possibility of having a more specific model for an individual taxi instead of a global model for all taxis in the traditional data mining approaches is a reality in the current hyperconnected transportation system.

However, this is not true for all taxis due to the lack of existence of enough data for creating an accurate model for all taxis. For example, in a sparse area of the city, like the area indicated in Fig. 1 with a circle, only a few observations is available for modeling. In this case, a collaborative data modeling would be a good solution to improve the quality of the model by using the data from other sources. The previous results [19, 20] confirm that there is potential in sharing data in the process of learning local models. For the prediction of the trip duration, different taxis can use different data like taxi’s data, data from taxi’s neighbors, data collected at the roadside unit, or the data which is collected throughout the city (different dimensions). Further, collaborative data modeling may improve the quality of the prediction in the cost of data communication.

On the other hand, various algorithms have been introduced which can be used for the prediction of trip duration. However, their performance varies and therefore causes several challenges. One of the important challenges in the area of data mining is that to discover for a specific problem which algorithm has the best performance. Yet, it has already been shown that there is no unique algorithm in which it has the best performance for a broad problem domain [21]. Therefore, the problem of algorithm selection is done either based on expert advice or a trial-and-error approach. Neither way is utterly satisfactory for the end user who wishes to access the technology cost-effectively [22].

A metalearning approach [23] is used in this paper to deal with these problems: (1) which algorithm should be used, and (2) when and with whom the data should be shared. Metalearning uses a machine learning algorithm to relating the algorithm’s performance to the data characterization. The contribution is also extended to (3) applying this collaborative data analysis to the problem of estimating of the taxi trip duration using the taxi dataset which is obtained from the Carnegie Mellon (CMU) Portugal project, DRIVE-IN (Distributed Routing and Infotainment through Vehicular Inter-networking) [24]. We also (4) discuss the use of this approach for other applications including manufacturing of products and supply chain management.

The rest of the paper is organized as follow. Section 2 explains the proposed approach and the results of the experiment. An extension of the approach is discussed in Sect. 3. Finally, Sect. 4 concludes the paper.

2 An Example of Collaborative Data Analysis in Hyperconnected Transportation System

In this section, a collaborative data analysis (Sect. 2.2) is introduced and applied to a dataset from hyperconnected transportation system (Sect. 2.1). Then, the proposed approach is evaluated on the dataset and the results are presented in Sect. 2.3.

2.1 Taxi Data

The data is collected from a large-scale scenario [24], from taxis in the city of Porto. Porto has an area of 41.3 km2, and contains 965 km of roads which make it the second largest city in Portugal. It has with more than one million inhabitants and is in a center of a metropolitan area. There are 441 taxis and 63 taxi stands in the city. Each taxi has a GPS receiver and can collect the log about each trip. The dataset consists of 5 months in 2013 for all the taxis. The dataset contains 13 data features characterizing events [24].

As an example of the scenario where the data is collected, Fig. 2 shows a snapshot of the taxis placements in the city of Porto. The green dots show the taxi positions in the city. The communication range for two taxis (red and black) is also shown by purple circles.

Fig. 2.
figure 2

Illustrative map of Porto, Portugal. The green dots are the initial taxi placement. The communication range for the red and the black taxi is shown by a purple circle around them. (Color figure online)

Full size image

There are five months data in 2013. Table 1 shows the number of taxis and the average number of observations for each taxi in each month. There are around 440 taxis and on average, there are between 1238–1484 observations for each taxi. The fourth and fifth columns also show the minimum and the maximum number of observations per each taxi, respectively. As it can be seen, there are taxis with few examples (2–14 observations). In these cases, data aggregation to use data from other taxis may be useful for modeling.

Table 1. A simple statistics about Taxi dataset
Full size table

2.2 Collaborative Data Analysis

As mentioned earlier, to improve the problem of algorithms selection and collaborative data modeling, we propose a metalearning approach which helps to select the right algorithm and the right part of data space for each individual taxi. In this section, we briefly describe the methodology which is summarized in Fig. 3.

Fig. 3.
figure 3

Methodology used for a collaborative data analysis in hyperconnected transportation systems

Full size image

The data collection is done within the DRIVE-IN project [24] (see Sect. 2.1). Then, the dataset is organized in hierarchy structure using two levels of hierarchy: the data associated with a taxi as local data and the data for the whole month as global data.

In the proposed model, at the first level, each taxi (\( T_{i} \)) makes a category, \( C_{i}^{1} , \forall i \in \{ 1, \ldots ,n_{1} \} \) where \( n_{1} \) is the number of taxis. The level two has only one category joining all the data from 440 taxis.

After forming the dataset in a customized format, \( DB = \left\{ {T_{i} ,C_{i}^{j} ,y_{i} } \right\}, \forall i \in \left\{ {1, \ldots ,440} \right\}, \forall j \in \{ 1,2\} \), it is passed to the base-level experiment. In the next step, each algorithm is applied on the data from both levels for each taxi.

At the base-level, four machine learning algorithms are applied to the data: support vector machines (SVMs) [25–27], random forest [25–27], decision tree [31–33], and linear regression [31, 32]. As a result, there are several performance indicators for each taxi: \( P_{ig}^{k} \) which indicates the performance of the algorithm \( g \) at level \( k \) for taxi \( i \).

$$ P_{iw}^{j} : \forall w \in \left\{ {1, \ldots ,4} \right\}, \forall j \in \left\{ {1,2} \right\}, \forall i \in \{ 1, \ldots ,440\} $$
(1)

Where \( w \) indicates the algorithms, \( i \) shows taxis, and \( j \) stands for levels.

In addition, for each taxi and at each level of the hierarchy, the metafeatures are calculated.

There are 31 metafeatures in which they describe the dataset’s structure. All the metafeatures that we used are briefly described in [36]. In general \( mf_{i}^{j} \) is the value of the metafeatures for the taxi \( i \) at the level \( j \). By comparing the performance indicators at the base-level for each taxi, the best one is selected according to the Eq. 2:

$$ P_{{best_{i} }} = \mathop {\hbox{max} }\limits_{w,j} (P_{iw}^{j} ), \forall w \in \left\{ {1, \ldots ,4} \right\}, \forall j \in \{ 1,2\} $$
(2)

The metadata consists of the taxi identification, metafeatures for both levels and the best performance indicator obtained from Eq. 2.

$$ T_{i} , mf_{i}^{1} ,mf_{i}^{2} ,P_{{best_{i} }} $$
(3)

The purpose of the metalearning is to discover the best algorithm and level to obtain the best performance. Consequently, the meta-level experiment maps the extracted metafeatures to the best performance obtained at the base-level (target variable at the meta-level).

Finally, the proposed model can recommend an algorithm and a level for each taxi that by applying the recommended algorithm on the suggested level, the best performance can be obtained (see Eq. 4).

$$ \begin{array}{*{20}l} {Model~input:\,T_{i} } \\ {Model~output:\,\{ recommended~level~\left( j \right),~recommended~algorithm~(g)\} } \\ \end{array} $$
(4)

More detail about the methodology used to obtain the results is presented in [36].

2.3 Evaluation

Base-Level Evaluation.

The problem of prediction of the trip duration at the base-level is a regression problem. Each trained model tries to predict the trip duration. This evaluation of the prediction is done by the Normalized Root-Mean-Square-Error (NRMSE). RMSE is a routinely used metric which indicates the differences between the actual observed value and the predicted value by a machine learning model. In addition, the NRMSE is calculated using the RMSE divided by the standard deviation (std) of the predicted variable (See Eqs. 5 and 6). We use the hydroGOF package [37] in R [38] to calculate the NRMSE.

$$ RMSE = \sqrt {\frac{{\sum {(\widehat{{Dt_{i} }} - Dt_{i} )^{2} } }}{{n_{1} }}} $$
(5)
$$ NRMSE = 100 *\frac{RMSE}{\sigma } $$
(6)

Where \( n_{1} \) is the number of predictions, \( \sigma \) is the std of the prediction values, \( Dt_{i} \) is the real trip duration, and \( \widehat{{Dt_{i} }} \) is the predicted trip duration. Considering the NRMSE values, the algorithm with the lowest NRMSE is chosen as the best one for each taxi and is used at the meta-level.

Meta-Level Evaluation.

The proposed framework at the meta-level predicts an algorithm and a level of granularity which have the lowest NRMSE for a selected taxi. As a result, the meta-level problem is a classification problem. This prediction is made based on metafeatures which describe the characterization of the dataset.

At the meta-level, the performance of the framework is evaluated by the accuracy of the model. Moreover, the performance of the proposed framework is also evaluated by comparing to the possible range of base-level performance. \( Scaled_{error} \) is a metric that shows the relative NRMSE of the metalearning framework with respect to the best and the worst NRMSE at the base-level. It is calculated by the following equation:

$$ Scaled_{error} = \frac{{NRMSE_{ML} - NRMSE_{B} }}{{NRMSE_{W} - NRMSE_{B} }} $$
(7)

Where \( NRMSE_{ML} \) is the NRMSE of the metalearning framework, \( NRMSE_{B} \) is the best NRMSE and \( NRMSE_{W} \) is the worst NRMSE at the base-level. Therefore, the range of \( Scaled_{error} \) is from 0 to 1. Furthermore, a lower \( Scaled_{error} \) shows a better performance at the meta-level.

2.4 Is Collaborative Data Analysis Useful?

In this section, we sum up the obtained results from the evaluation part of our methodology.

Base-Level Results.

As previously mentioned (Sect. 2.3), the performance of the base-level is evaluated by NRMSE. Figure 4(a) is the box-plot of the average NRMSE for each taxi for each month. It is clear that the NRMSE is less than 5 % for all months. The average NRMSE is approximately 1 % for each month. So, the base-level error is around 1 % on average which sounds significantly good. These results show that at the base-level, the models can predict the trip duration very precisely.

Fig. 4.
figure 4

Evaluation results (Color figure online)

Full size image

Meta-Level Results.

As discussed previously (Sect. 2.3), our metric to evaluate the meta-level results is \( Scaled_{error} \). Figure 4(b) shows this metric on average for all months. As it can be seen, the \( Scaled_{error} \) is about 30 % in the worst scenario and around 5 % for the best one. The meta-level results (the blue line) are much better than the baseline results (the green line). The baseline is the majority best solution at the base-level which is a combination of an algorithm and a level for each taxi that has the best performance. Generally speaking, the results show that during the raining months (February to April) in Porto, when there are more taxi trips in the city, the meta-level is more accurate than the months that there are fewer taxi trips (May and June) due to lack of enough data for building a model. In this case, it is recommended to use the global model to have an accurate model.

Meta-Level vs Base-Level Results.

The comparison results between the meta-level and the base-level show that the performance of the algorithms selected by the meta-model is near the best performance obtained at the base-level (Fig. 4(c)). The performance of the suggested solution by the meta-level (the blue and the cyan line) is almost close to the best performance at the base-level (the green line) while is better than the baseline performance (the black line). This satisfies our objectives.

Finally, the comparison of accuracy between the baseline (the black line) and the meta-level (the blue line) is illustrated in Fig. 4(d). According to these results, the performance of the meta-level exceeds the performance of the baseline for all months.

3 Discussion

The proposed approach in this paper helps to identify the best solution for the problem of prediction of taxi trip duration to improve the taxi utilization and passenger satisfaction. Using the hyperconnected intelligent systems, this proposal can be used by different applications including manufacturing of products by forecasting of product demands, supply chain management by predicting of the best location of stocks, and real-time optimization of supply chain networks by prediction of the best route for fleets, through networking machinery, sensors and control systems together.

All manufacturers have a desire to give their consumers exactly what they want. This can be done by using past data collected from sales and production lines and forecasting the demand for a product. Our proposed approach can be implemented in this case by organizing the past data into hierarchy structure. One of possible solution can be using three different hierarchy levels: the data associated with a product, the data related to a group of products which have the same type, i.e. foods, clothes, and so on, and all the data.

Another example is supply chain management where a poor stock’s location can give low productivity, unreliable deliveries of materials, high costs, and poor customer service. The same approach can be done using the data that can be collected from the logistics and also stocks movement within the supply chain. The approach can help to deal with the uncertain and non-stationary demand with minimum cost.

The hyperconnected networks and IoT present excellent possibilities for businesses to conduct through evolution and innovation. For this purpose, companies need to be aware of the changing of the business dynamics caused by innovation.

4 Conclusion

The existence of hyperconnected networks can make a revolution in the public transportation systems. High resource utilization and customer satisfaction are two major metrics which can be achieved using hyperconnected networks and machine learning approaches. In this paper, a metalearning proposal is introduced for the prediction of taxi trip duration to improve the taxi utilization and passenger’s satisfaction by using a collaborative data analysis. The proposed approach aims at assisting taxi companies, passengers, and the public authorities for better distributing taxis to the taxi stands and determining the best route for the taxi trips using appropriate learning algorithm for the prediction of taxi trip duration. The experiments are carried out on the data collected in the Drive-In project. Several models are obtained from two levels of granularity: taxi itself and whole taxis. The results demonstrate that the proposed metalearning framework can help recommending an algorithm with the best performance at the base-level with high accuracy and outperforms the baseline accuracy. Furthermore, the performance of the base-level is also substantially adequate. In overall, the metalearning forecasts the duration of the taxi trip with the error rate less than 5 %.

As interesting future works, this approach can be extended to other parts of the hyperconnected networks, i.e. manufacturing of products and supply chain management, as discussed in Sect. 3.