Beyond the Boundaries of SMOTE

Abstract

Problems of class imbalance appear in diverse domains, ranging from gene function annotation to spectra and medical classification. On such problems, the classifier becomes biased in favour of the majority class. This leads to inaccuracy on the important minority classes, such as specific diseases and gene functions. Synthetic oversampling mitigates this by balancing the training set, whilst avoiding the pitfalls of random under and oversampling. The existing methods are primarily based on the SMOTE algorithm, which employs a bias of randomly generating points between nearest neighbours. The relationship between the generative bias and the latent distribution has a significant impact on the performance of the induced classifier. Our research into gamma-ray spectra classification has shown that the generative bias applied by SMOTE is inappropriate for domains that conform to the manifold property, such as spectra, text, image and climate change classification. To this end, we propose a framework for manifold-based synthetic oversampling, and demonstrate its superiority in terms of robustness to the manifold with respect to the AUC on three spectra classification tasks and 16 UCI datasets.

1 Introduction

In problems such as radioactive threat classification, oil spill classification, gene function annotation, medical and text classification, the class distribution is imbalanced and the minority class is rare [5, 6, 18]. Rarity, in this sense, breaks the general assumption of machine learning that demands a representative set of instances from each class. Failure to satisfy this leads to the induction of a decision boundary that is biased in favour of the majority class, thereby causing weak classification accuracy [15, 25]. Given the practical importance, and the significant challenge posed by domains of this nature, class imbalance has been identified as one of the essential problems in machine learning [26] and has spawned workshops, conferences and special issues [8, 9].

The obvious solution to this problem is more training samples. This is not possible in cases of imbalance arising due to domain properties, such as acquisition cost and class probability. Thus, we turn to the generation of synthetic instances based on the available training instances. Within class imbalance, this is known as synthetic oversampling, and was originally devised to compensate for the weakness of random oversampling [10].

Synthetic oversampling offers a means of balancing the training classes without discarding useful instances from the majority class via random undersampling and without risking overfitting by replicating examples with random oversampling. Instead, the training instances that belong to the minority class are used as the foundation from which to synthesize additional training instances. This avoids overfitting and effectively expands the minority space. How the space is expanded depends on the bias of the synthetic oversampling method, which dictates the way in which the probability mass of the training instances is spread through the feature space.

The state-of-the-art methods in synthetic oversampling are based on the SMOTE algorithm. The two major criticisms of SMOTE are that in some cases it synthesizes instances inside the majority class, thus causing the induced classifier to overcompensate by pushing the decision boundary into the majority space, and in other cases it does not synthesize instances close enough to the majority class. This results from the fact that the instances are synthesized in the convex-hull formed by the minority training points [3]. These negative effects grow quickly with absolute imbalance and dimensionality. In a well-sampled low-dimensional dataset, SMOTE can be expected to interpolate synthetic points between training instances that are in the same local neighbourhood of the feature space. Therefore, the likelihood that the synthetic instances are representative of the latent distribution is high. When there are very few samples of the class, however, the samples are more likely to be dispersed around the feature space. Thus, interpolating synthetic instances between them is likely to be error prone.

In an attempt to manage this, a set of ad-hoc modifications have been proposed to remove minority instances generated in the majority space, whilst others have been proposed to promote the generation of instances close to the majority space [2, 3, 14, 20]. We see these alternatives as addressing symptoms resulting from a generative bias that is inappropriate for the data rather than treating the root cause of the weaknesses. Specifically, these methods have been designed and applied without giving consideration to properties of the data to which that are applied.

Fig. 1.

Left: Training instance. Right: Approximating a sine function with and without prior knowledge.

In order to maximize the likelihood of generating effective instances from a small training set, we argue that it is essential to design synthetic oversampling methods with biases that match the properties of the target data. The benefit of the correct bias is effectively demonstrated with the analogous problem of inducing a representative function from the training data in Fig. 1. To induce a function, like a generative model, we start with a bias, such as a linear or non-linear function, and a set of free parameters that accompany the bias. The induction process quantifies the free parameters so that they best fit the training data. Selecting the correct bias, in the case of our example, a sine function, increases our likelihood of inducing a good representation, whereas selecting an incorrect bias, such as a linear function with Gaussian noise, will produce a very weak approximation. Similarly, utilizing an incorrect bias in the context of synthetic oversampling can lead to inaccurate synthetic instances that negatively impact classifier induction.

Based on our practical experience in applying synthetic oversampling methods to gamma-ray spectral classification problems, we were able to identify the manifold property as one that has a negative impact on the existing methods. A dataset conforms to the manifold property when its probability density resides in a lower-dimensional space that is embedded in the feature space [7]. The embedded space is thus constructed by combining a subset of features from the feature space. For data that conforms to the manifold property, the embedded representation offers a more concise form than the feature space, much like the grammar and syntax of a programming language provide a much more concise representation of the program to the computer than the pseudo code intended for human consumption. Whilst the embedded space resulting from manifold learning is a form of dimension reduction, it is much more than simple feature selection. Feature selection can, at best find, a subset of the existing features in the feature space. Alternatively, manifold learning discovers a completely new set of features to better represent the data.

Data with the manifold property is common within a diverse set of machine learning domains, ranging from global climate change to medicine. The bias applied by SMOTE uses the straight line distance between training points in the minority class. This is generalized as the Minkowski distance, which is an inaccurate measure for manifolds. Therefore, choosing SMOTE to synthetically oversample data that conforms to the manifold property is similar to choosing a linear model to represent the sine function in Fig. 1; the best we can hope for is synthetic data that is very weakly related to the target distribution. To address this, we propose a framework for synthetically oversampling data that conforms to the manifold property.

The contributions of this paper include: (1) identifying a general weakness in synthetic oversampling methods on data that conforms to the manifold property, (2) illustrating the cause of this weakness for SMOTE, (3) articulating the benefit of synthetic oversampling with a manifold bias, (4) proposing a framework for manifold-based synthetic oversampling, and (5) demonstrating the superiority of the framework using two distinct formalization on artificial data, gamma-ray spectra data and UCI data that conforms to the manifold property.

2 Problem Overview

Our research was originally inspired by our collaboration with the Radiation Protection Bureau at Health Canada where we applied machine learning for safety in regards to radiation. The primary challenges were the high-dimensionality of the domain and the degree of imbalance. These are features that are common to a large number of classification domains, such as global climate change, image recognition, human identification, text classification and spectral classification.

We recognized that domains with this property can often be better represented in a lower-dimensional embedded space. This concept takes advantage of the reality that instances are not spread throughout the feature space but are concentrated around a lower-dimensional manifold. A simple example of a manifold in machine learning comes from handwritten digit recognition, where the digits are recorded in a high-dimensional feature space, but can be effectively represented in a lower-dimensional embedded space that encodes the various orientations and rotations of the digit [12]. Thus, manifold learning provides a gateway to the embedded space in which all possible handwritten digits can be encoded.

A significant amount of research has been dedicated to the development of manifold learning methods [17]. The resulting algorithms utilize a diverse set of assumptions and biases, such as the complexity of the curvature of the manifold and the nature of the noise. Classic methods such as PCA and MDS are simple and efficient. These are guaranteed to determine the structure of the data on or near the embedded manifold. These traditional methods assume a linear manifold [21]. Other, more algorithmically complex methods, such as kernel PCA and autoencoding, enable the induction of non-linear manifolds. Manifold learning has demonstrated great potential in clustering, classification and dimension reduction [4, 23, 27]. However, in spite of their potential, manifold learning methods have gone unconsidered in problems of class imbalance. We address this gap in the literature with a framework for manifold-based synthetic oversampling.

We illustrate the weaknesses of SMOTE using a one-dimensional manifold embedded in a two-dimensional space. This is visualized in Fig. 2. Because the more recent methods that have been proposed to improve SMOTE all apply the same bias, they suffer from the same weaknesses on data that conforms to the manifold property. For this reason, when we refer to SMOTE, we intend for it to include its derivatives.

The top left graphic in Fig. 2 shows the manifold in red with samples from the manifold appearing as black circles. Each instance can be represented by its one-dimensional coordinate m in the manifold space. In machine learning, we often have data in the feature space, not the embedded space. Manifold learning induces a model of the embedded space, and from this we can focus the generation of instances in high probability regions. This is visualized in the top right graphic where the blue shading illustrates the probability mass being spread along the manifold. In the subsequent section, we demonstrate how this is achieved with our proposed framework.

Fig. 2.

Erroneous spread of instances away from the manifold with SMOTE.

The bottom graphics demonstrate the result of synthetic oversampling with SMOTE with $k=7$ and $k=3$. It balances the training set by interpolating points between k nearest neighbours in the minority training set [10]. As a result, the k value indirectly affects the area covered by the convex hull. The convex hull is represented by the blue area. A larger k value will uniformly spread points over a larger area, whereas a smaller k value creates dense, small clusters of synthetic points. This is emphasized with the shading of the convex hulls.

SMOTE uses the straight line distance to calculate the kNN set for each instance in the minority class, and generates new instances at random points on the edges connecting these neighbours. Due to the topological structure of a manifold, this will only produce an accurate kNN set if the query instances are close together [13]. In problems of class imbalance there are few minority training instances and as a result, this is unlikely to occur. When SMOTE is applied in this context, the convex-hull can extend away from the manifold. In our example, we see that it extends well below the red line representing the latent distribution that we hope to synthetically oversample.

3 Framework

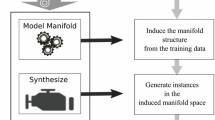
Figure 3 presents the three components of our framework for manifold-based synthetic oversampling. Our objective is to provide a standalone synthetic oversampler. Therefore, although the data is generated in a hidden embedded space, it is provided to the user in the original feature space. Subsequently, the user can apply a pre-processing method that is appropriate for the classifier.

The first element of the framework induces a manifold representation of the minority class via a well-suited method, such as PCA, kernel PCA, autoencoding, local linear embedding, etc. Data is synthesized along the induced manifold during the second phase of the framework, and the final phase maps the synthesized data to the original feature space and returns it to the user.

Fig. 3.

General framework for synthetic oversampling.

The number of training examples and the complexity of the latent manifold are two factors to consider when selecting a manifold learning method to employ in the framework. If the learning objective involves a linear manifold, or the training data is extremely rare, a linear method is appropriate. Alternatively, non-linear problems with more training data are well-suited for methods that can represent the complexity. Our experiments focus on PCA and denoising autoencoder because together they can model linear and non-linear manifolds that are simple or complex. Moreover, they offer effective and easy-to-implement means of sampling from the induced manifold.

Formalization with PCA: PCA is a linear mapping from the d-dimensional input space to a k-dimensional embedded space where $k\ll d$. The standard process is a result of calculating the leading eigenvectors E corresponding to the k largest eigenvalues $\lambda$ from the sample covariance matrix $\mathbf {\varSigma }$ of the target data.

In the PCA realization of the framework, a model $pca = \{\mathbf {\mu }, \varSigma , E, \lambda \}$ of the d-dimensional target class T with m instances is produced. We produce a synthetic set S of n instances in the manifold-space by randomly sampling n instances from $T^\prime = T \times E$ (T in the PCA-space) with replacement. In order to produce unique samples on the manifold, we apply i.i.d. additive Gaussian noise $\mathcal {N}\big (0, \mathcal {I}\big )$ to each sampled instance prior to adding it to the synthetic set S. The covariance matrix for the Gaussian noise is a diagonal matrix with each $\sigma _{i,i}$ specified by $\beta \lambda _i$, where $\beta$ is the scaling factor applied to the eigenvalues. This controls the spread of the synthetic instances relative to the manifold, and can be thought of as a geometric transformation of points along the manifold, thereby producing new synthetic samples on the manifold. Finally, we map the synthetic instances S into the feature space as $S^\prime = S\times E^{-1}$ and return them to the user for use in classifier induction.

Formalization with Autoencoders: Autoencoders are a form of artificial neural networks commonly used in one-class classification [16]. They have an input layer, hidden layer and output layer, with each layer connected to the next via a set of weight vectors and a bias. The input and output layers have a number of units equal to the dimensionality of the target domain, and the user specifies an alternate dimensionality for the hidden space. The learning process involves optimizing the weights used to map feature vectors from the target class into the hidden space and those used to map the data from the hidden space back to the output space.

Fig. 4.

Three steps of synthesization for the autoencoder formalization with generic points and handwritten 4s. (Color figure online)

A manifold bias is incorporated in the autoencoding process through its mapping from the feature space to the hidden-space and back via $f_{\theta }(\cdot )$ and $g_{\theta ^\prime }(\cdot )$, where:

$$\begin{aligned} \begin{aligned} f_{\theta }(x)&= s(\mathbf {W}x + b) \\ g_{\theta ^\prime }(y)&= s^\prime (\mathbf {W^\prime }y + b^\prime ). \end{aligned} \end{aligned}$$

(1)

Here, $\theta$ and $\theta ^\prime$ represent the induced encoding and decoding parameter set, respectively. Specifically, $\mathbf {W}$ is a $d\times d^\prime$ weight matrix and b is a d-dimensional bias vector. The function s, is a non-linear squashing function, such as the sigmoidal. In the decoding parameter set, $\mathbf {W^\prime }$ and $b^\prime$ represent the weight matrix and the bias vector that cast the encoded vector back to the original space. The $s^\prime$ function is typically linear in autoencoders. As is standard with artificial neural networks, the weights are learnt using backpropagation and gradient descent. In addition, we utilize denoising during the training process as a form of regularization to promote the learning of key aspects of the input distribution [24]. We add Gaussian noise to the input and the network learns to reconstruct the clean instances.

The learning processes prioritizes the dual objective of a reconstruction function $g(f(\cdot ))$ that is as simple as possible, but capable of accurately representing neighbouring instances from the high-density manifold [1]. This promotes accurate reconstruction of points on the manifold, whilst the reconstruction error $|x-g(f(x))|^2$ rises quickly for examples orthogonal to the manifold. Given a point, p, on the manifold, the output g(f(p)) remains on the manifold in essentially the same location. Conversely, when an arbitrary point, q, is sampled from off the manifold, the output g(f(q)) is mapped orthogonally to the manifold. This is demonstrated in Fig. 4 as $g(f(\tilde{x})) \rightarrow x$, where $\tilde{x}$ is a point off the manifold, with the manifold depicted in red.

The mapping $g(f(\tilde{x})) \rightarrow x$ is key to the formalization of the autoencoder version of our framework. The basic objective is to induce the manifold representation of the minority class and use its ability to perform orthogonal mappings to the manifold to generate samples. Generally speaking, we take an arbitrary minority class instances x, apply a non-orthogonal mapping off the manifold $x \rightarrow \tilde{x}$ and map it orthogonally back to the manifold via $g(f(\tilde{x})) \rightarrow y$. The result is a transformation along the manifold from a training instances x to synthetic instances y. This is illustrated graphically in Fig. 4. The non-orthogonal mapping is produced by adding noise to the training instance x. A greater amount of noise leads to a larger transformation along the manifold. By sampling n instances from the minority class with replacement and performing the transformation, we produce the synthetic set. We note that $g(\cdot )$ maps the synthetic set returned to the user into the target feature space. Algorithm 1 formalizes the method.

Prior to calling Algorithm 1, we perform model selection with the reconstruction error by randomly searching the parameter-space using the minority training data $\mathcal {X}$. This facilitates a simple and effective form of model selection and is the standard means of model selection for autoencoders. Nonetheless, we are exploring alternate forms of model selection for this novel application of the autoencoder. The model selection process of the autoencoder provides the ability to set the free parameters according to the target class, whereas this is not possible with the SMOTE-based methods. As a result, the user cannot know if they have specified a good value for k until they apply the classifiers after synthetic oversampling.

Given the few training instances in problems of class imbalance, we prefer a simple model rather than an overly complex model of the manifold. To encourage this, we conduct the parameter search over a relatively small number of hidden units and training epochs. For the spectra data, we searched 5–30 hidden units with fewer than a thousand epochs of training.

Computational Overhead: The degree to which the framework will add computational overhead depends on the manifold learning method selected. Building a PCA model, for example, requires eigenvalue decomposition of the covariance matrix of the feature vectors. Using Jacobis method for diagonalization requires $\mathcal {O}(d^3 + d^2m)$ computations; however, the efficiency can be improved [19]. More sophisticated manifold learning methods, such as autoencoders, that involve iterative learning can take longer. The key point to remember here is that learning is being performed on a small training set. This significantly limits the training time because there are few examples to look at, and we want to avoid overfitting. This applies to SMOTE as well. Although SMOTE has the potential to be very slow due to its nearest neighbour search, the small training set means that, in practice, it is reasonable fast. Unlike our proposed framework, however, the adaptions of SMOTE take significant performance hits because they search for nearest neighbours in the entire training set.

4 Gamma-Ray Spectral Classification

Spectra classification for the Radiation Protection Bureau at Health Canada sparked our initial interest in the relationship between manifolds and synthetic oversampling.

4.1 Data

Two gamma-ray spectra datasets from the Canadian national environmental monitoring system, and one collected as part of event security at the Vancouver Olympics are utilized in our experiments. The environmental monitoring datasets were recorded at Thunder Bay and Saanich. These cities were selected for testing because they are geographically, geologically and atmospherically very distinct. This provides for very distinct data distributions.

During a four month period, 19, 112 spectra were recorded at Saanich, 44 of which were from the minority class. At Thunder Bay, 11, 602 spectra instances were recorded, with 29 belonging to the minority class. The Vancouver Winter Games data was recorded and monitored to ensure that no radioactive material entered the venue. There are 39, 000 background instances in the dataset and 39 isotopes of interest in the minority class. The two environmental datasets are 250-dimensional and the Vancouver data is 500-dimensional.

Through discussions with our colleagues at the Radiation Protection Bureau at Health Canada, we inferred the conformance of this data to the manifold property. In particular, we know that the radioactive occurrences that form the minority class will affect subset specific energy levels in the spectra, forming an embedded space.

4.2 Evaluation

We utilize the SVM, MLP, kNN, naïve Bayes and decision tree classifiers in the following experiments. Synthetic oversampling is performed by the autoencoder and PCA formalizations of the framework. These are compared to SMOTE and SMOTE with the removal of Tomek links [22]. The latter is performed in order to remove synthetic instances generated in, or too close to, the majority class. This will potentially assist SMOTE by removing erroneously synthesized instances.

We perform $5 \times 2$-fold cross validation and report the mean and standard deviations of the AUC performance. This form of cross validation method is ideal for large datasets such as these, and has been shown to have lower probability of issuing a Type I error as compared to k-fold cross validation [11].

4.3 Experimental Results

The mean and standard deviation of the AUC after the application of manifold-based synthetic oversampling and SMOTE-based synthetic oversampling is reported for each classifier on each dataset in Table 1. We specifically show the results of the best manifold-based (PCA or autoencoder) and SMOTE-based (SMOTE or SMOTE with the removal of Tomek links) synthetic oversampling implementation in these tables. This is done to emphasize the relative performance of the two approaches, and shows that the manifold-based framework is superior on the gamma-ray datasets. The combination of the manifold-based method with each classifier produces higher mean AUCs on the Vancouver and Thunder Bay datasets. This is also the case on the Saanich dataset for all except with the SVM classifier. In addition, we report the mean AUC across all classifiers. This shows that our framework is generally superior regardless of the classifier.

Table 1. The mean AUC results for each method on the gamma-ray dataset.

With respect to the specific methods, the autoencoder formalization is better than PCA on the Vancouver and Saanich datasets, whereas the PCA implementation is superior on the Thunder Bay dataset. Interestingly, SMOTE is always the better than its counterpart using the removal of Tomek links.

5 UCI Classification

In order to generalize our findings, we now shift to examine the impact of the manifold on synthetic oversampling over benchmark datasets from the UCI repository. To paint a clearer picture of the impact of the manifold, we artificially control the degree of conformance of the datasets to the manifold property. This is done using a process that we refer to as manifold augmentation, which we detail later in this section. Performing manifold augmentation on the UCI datasets enables us to run experiments where we gradually increase the conformance in order to witness the impact of the manifold on each synthetic oversampling method, whilst holding the other aspects of complexity, such as modality and overlap, constant. This enables us to demonstrate the causal link between the increase in conformance and the change in performance.

5.1 UCI Data

The sixteen UCI datasets specified in the first column of Table 3 were selected to ensure a diverse range of dimensionalities and complexities. When required, the datasets are converted to a binary task by selecting a single class to form the minority class, and the remaining classes are merged into one.

For each experiment, we train on 25 minority training instances and 250 majority training instances; thus, we render each domain as an imbalanced classification task involving the concept of absolute imbalance. We have selected constant values for the training distribution, rather then specifying a percentage for the minority class, in order to ensure that the performance differences between datasets are not the result of having access to different numbers of minority instances. If we set the minority portion to $10\,\%$, for example, then a dataset with 1, 000 instances would have many more examples in the training set than a dataset with 200 instances. This can have a great impact on performance. Finally, we perform a series of augmentations to each dataset to increasingly strengthen the conformance to the manifold property.

5.2 Manifold Augmentation of UCI Data

Our manifold augmentation process is contingent on the notion that the probability mass resides in a lower-dimensional space. We introduce this by adding columns of uniformly distributed random variables that span both classes to the data matrix. In this case, the augmentation is suggestive of a feature selection problem; however, feature selection is not an effective means of solving manifold problems. This is because they will only find a subset of the features. A manifold space is a more general subspace that is formed from combinations of the original features. These combinations may be simple linear combinations:

$$\begin{aligned} f^\prime _i = a_1f_1 + a_2f_2 +\,... +\,a_df_d, \end{aligned}$$

(2)

where $f^\prime _i$ $i \in \{1,..,k\}$ is one of k components of the manifold-space embedded in the d-dimensional feature space; other manifolds are formed of much more complex combinations. In these cases, no subset of the original feature-space will represent the manifold.

5.3 Evaluation

In this set of experiments, we apply the same synthetic oversampling methods that were used in the previous section to balance the training sets prior to the application of the five classifiers. Our primary interest in this set of experiments is to elicit the affect of the manifold. In order to achieve this, we apply the augmentation method described above, in which each UCI dataset is augmented to increase conformance to the manifold property with:

$$\begin{aligned} p=\{0\,\%,15\,\%,30\,\%,45\,\%,60\,\%,75\,\%,90\,\%\}, \end{aligned}$$

(3)

where $p=0\,\%$ is the unchanged UCI data and $p=90\,\%$ returns a modified dataset with the dimensionality increased by $90\,\%$. Therefore, for each of the 16 UCI datasets, we create 7 augmented versions, where the increasing p values indicates increasing conformance to the manifold assumption.

Thirty repeated trials are run for each augmented dataset. Because we have limited space and we interested in studying the impact of the manifold, we record the mean performance for each synthetic oversampling method on each dataset and calculate the average over all of the classifiers (similar to what we reported in the last row for Table 1). We provide these aggregated results to demonstrate the relative strength of our proposed method. Our analysis of the individual classifiers is postponed for a longer paper.

The first set of results reports the ranking of each synthetic oversampling method based on the AUC. The rankings are tabulated for the performance on the original UCI datasets ($p=0$) and for the mean of the AUC produced on the augmented datasets ($p=\{15,..,90\}$). This demonstrates how the relative performance of the methods changes when conformance to the manifold assumption is increased up to $p=90$.

In the second set of experiments, we include only the best manifold-based method and SMOTE-based method for each dataset in our results. We compare the change in the performance resulting from the increased conformance to the manifold property from $p_0$ to $p_{90}$. We refer to this as the loss score for each dataset D, where:

$$\begin{aligned} loss(D_{p_0}, D_{p_k}) = \overline{AUC(D_{p_0})} - \overline{AUC(D_{p_k})}. \end{aligned}$$

(4)

This shows the degradation caused by the manifold. If the manifold has no impact, then the loss score is zero. The loss score increases with the relative impact of the manifold

5.4 Experimental Results

AUC Results: Table 2 presents the number of times each synthetic oversampling system produced the highest mean AUC on the UCI datasets. In the case of a tie between two methods, 0.5 is attributed to each. The first column ($p=0$) refers to the original UCI datasets, and the last column shows the results after augmentation with $p=\{15, .., 90\}$. In both cases, the manifold-based methods are superior. For $p=0$ the manifold-based methods are better $7+4=11$ times out of 16 and tied once with a SMOTE-based method. The real strength of the manifold-based method, however, is shown when the conformance to the manifold property is increased. The manifold-based methods are always better when the conformance to the manifold property is increased. Specifically, the autoencoder is the best on 13 of the 16 datasets and PCA is superior on the others.

Table 2. Total number of AUC wins for each synthetic oversampling method on the augmented UCI data.

Table 3. The degradation between $p=0$ and $p=90$ of the classifiers after the application of synthetic oversampling.

Loss Results: Table 3 displays the mean loss values for the manifold-based system and the SMOTE-based system on the 16 UCI datasets. Specifically, we report the loss for each dataset with respect to $loss(D_{p_0},D_{p_{90}})$ as described in Eq. 4. Fourteen of the sixteen datasets have lower loss scores when the manifold-based system is applied; these are highlighted in grey. This shows that in addition to its superiority in terms of the AUC, the proposed framework is more robust with respect to loss caused by the manifold. Specifically, the manifold causes less of a decrease in performance for the manifold-based approach than it causes for SMOTE.

6 Conclusion

We demonstrate that the existing methods of synthetic oversampling based on SMOTE do not achieve their full potential on data that conforms to the manifold property, and argue that a manifold-based approach to synthetic oversampling is required. We address this by proposing a framework for manifold-based synthetic oversampling, which enables users to incorporate the wide variety of methods from manifold learning into the framework. We demonstrate the framework with a PCA and autoencoder formalization. These are selected for their simplicity in use and their abilities to represent a wide variety of manifolds.

We show that the implementations outperform the SMOTE-based methods in terms of the AUC on three gamma-ray spectra datasets that conform to the manifold property. In order to generalize our findings, we use 16 UCI datasets and show that the framework outperforms SMOTE in terms of the AUC and that it is more robust to the manifold property in terms of the loss score. In addition to its strength on data that conforms to the manifold property, these experiments suggest that the framework is generally a good choice for synthetic oversampling.