Aggregating Crowdsourced Ordinal Labels via Bayesian Clustering

Abstract

Crowdsourcing allows the collection of labels from a crowd of workers at low cost. In this paper, we focus on ordinal labels, whose underlying order is important. Crowdsourced labels can be noisy as there may be amateur workers, spammers and/or even malicious workers. Moreover, some workers/items may have very few labels, making the estimation of their behavior difficult. To alleviate these problems, we propose a novel Bayesian model that clusters workers and items together using the nonparametric Dirichlet process priors. This allows workers/items in the same cluster to borrow strength from each other. Instead of directly computing the posterior of this complex model, which is infeasible, we propose a new variational inference procedure. Experimental results on a number of real-world data sets show that the proposed algorithm is more accurate than the state-of-the-art, and is more robust to sparser labels.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In many real-world classification applications, acquisition of labels is difficult and expensive. Recently, crowdsourcing provides an attractive alternative. With platforms like the Amazon Mechanical Turk, cheap labels can be efficiently obtained from non-expert workers. However, the collected labels are often noisy because of the presence of inexperienced workers, spammers and/or even malicious workers.

To clean these labels, a simple approach is majority voting [14]. By assuming that most workers are reliable, labels on a particular item are aggregated by selecting the most common label. However, this ignores relationships among labels provided by the same worker. To alleviate this problem, one can assume that labels of each worker are generated according to an underlying confusion matrix, which represents the probability that the worker assigns a particular label conditioned on the true label [7, 19]. Others have also modeled the difficulties in labeling various items [2, 13, 23–25] and workers’ dedications to the labeling task [2].

On the other hand, besides the commonly encountered binary and multiclass labels, labels can also be ordinal. For example, in web search, the relevance of a query-URL pair can be labeled as “irrelevant”, “relevant” and “highly-relevant”. Unlike nominal labels, it is important to exploit the underlying order of ordinal labels. In particular, adjacent labels are often more difficult to differentiate than those that are further apart.

To solve the aforementioned problem, Lakshminarayanan and Teh [16] assumed that the ordinal labels are generated by the discretization of some continuous-valued latent labels. The latent label for each worker-item pair is drawn from a normal distribution, with its mean equal to the true label and its variance related to the worker’s reliability and the item’s difficulty. While this model is useful for “good” workers, it is not appropriate for malicious workers whose labels can be very different from the true label. Moreover, it can be too simplistic to use only one reliability (resp. difficulty) parameter to model each worker (resp. item).

A more recent model is the minimax entropy framework [26], which is extended from the minimax conditional entropy approach for multiclass label aggregation [25]. To encode ordinal information, they compare the worker and item labels with a reference label that can take all possible label values. The confusion for each worker-item pair as obtained from the model is then constrained to be close to its empirical counterpart. Finally, the true labels and probabilities are obtained by solving an optimization problem derived from the minimax entropy principle. In comparison with [16], ordering of the ordinal labels is now explicitly considered.

In crowdsourcing applications, some workers may only provide very few labels. Similarly, some items may receive very few labels. Parameter estimation for these workers and items can thus be unreliable. To alleviate this problem, one can consider the latent connections among workers and items. Intuitively, workers with similar characteristics (e.g., gender, age, and nationality) tend to have similar behaviors, and similarly for items. By clustering them together, one can borrow strength from one worker/item to another. Kajino et al. [12] formulated label aggregation as a multitask learning problem [8]. Each worker is modeled as a classifier, and the classifiers of similar workers are encouraged to be similar. However, the ground-truth classifier, which generates the true labels, is required to lie in one of the worker clusters. Moreover, this algorithm requires access to item features and cannot be used with ordinal labels. Venanzi et al. [21] proposed to cluster multiclass labels by using the Dirichlet distribution. However, the number of clusters needs to be pre-specified, which may not be practical. Moreover, item grouping is not considered. Lakkaraju et al. [15] modeled both item and worker groups. However, they again require the use of both worker and item features. Moreover, clustering and label inference are performed as separate tasks.

In this paper, motivated by the conditional probability derived in the dual of [26], we propose a novel algorithm to aggregate ordinal labels. Different from [26], a full Bayesian model is constructed, in which clustering of both workers and items are encouraged via the Dirichlet process (DP) [9] priors. DP is a nonparametric model which is advantageous in that the number of clusters does not need to be pre-specified. The resultant Bayesian model allows detection of clustering structure, learning of worker/item characteristics and label aggregation be performed simultaneously. Empirically, it also significantly outperforms the state-of-the-art. However, as we use DP priors with non-conjugate base distributions, exact inference is infeasible. To address this problem, we extend the techniques in [11], and derive a mean field variational inference algorithm for parameter estimation.

2 Ordinal Label Aggregation by Minimax Conditional Entropy

Let there be N workers, M items, and m ordinal label classes. We use i, j, m to index the workers, items, and labels, respectively. The true label of item j is denoted $Y_j$, with probability distribution Q. The label assigned by worker i to item j is $X_{ij}$, and $\varXi$ is the set of (i, j) tuples with $X_{ij}$’s observed. We assume that there is at least one observed $X_{ij}$ for each worker i, and at least one observed $X_{ij}$ for each item j.

Zhou et al. [26] formulated label aggregation as a constrained minimax optimization problem, in which $H(X|Y) - H(Y) - \frac{1}{\alpha }\varOmega (\xi ) - \frac{1}{\beta }\varPsi (\zeta )$ is maximized w.r.t. $P(X_{ij} = k\;|\;Y_j = c)$ and minimized w.r.t. $Q(Y_j = c)$. Here, H(X|Y) is the conditional entropy of X given Y, H(Y) is the entropy of Y, $\varOmega (\xi ) =\sum _{i,s} (\xi _{is}^{\vartriangle ,\triangledown })^2, \varPsi (\zeta )=\sum _{j,s} (\zeta _{js}^{\vartriangle ,\triangledown })^2$ are $\ell _2$-regularizers on the slack variables $\xi _{is}^{\vartriangle , \triangledown }, \zeta _{js}^{\vartriangle ,\triangledown }$ (in (1) and (2)), and $\alpha , \beta$ are regularization parameters. Let $\phi _{ij}(c,k) = Q(Y_j = c)P(X_{ij}= k|Y_j = c)$ be the expected confusion from label c to label k by worker i on item j, and $\hat{\phi }_{ij}(c,k) = Q(Y_j=c)\mathbb {I}(X_{ij} = k)$ be its empirical counterpart. Besides the standard normalization constraints on probability distributions P and Q, Zhou et al. [26] requires $\phi _{ij}(c,k)$ be close to the empirical $\hat{\phi }_{ij}(c,k)$:

$$\begin{aligned} \sum _{c\vartriangle s} \sum _{k{\triangledown }s} \sum _j [\phi _{ij}(c,k) - \hat{\phi }_{ij}(c,k)] = \xi _{is}^{\vartriangle , \triangledown },&\forall i, \forall 2 \le s \le m, \end{aligned}$$

(1)

$$\begin{aligned} \sum _{c\vartriangle s} \sum _{k\triangledown s} \sum _i [\phi _{ij}(c,k) - \hat{\phi }_{ij}(c,k)] = \zeta _{js}^{\vartriangle , \triangledown },&\forall j, \forall 2 \le s \le m. \end{aligned}$$

(2)

Here, s is a reference label for comparing the true label c with worker label k, and $\vartriangle , \triangledown$ is a binary relation operator (either $\ge$ or <). Together, they allow consideration of the four cases: (i) $c< s, k < s$; (ii) $c < s, k \ge s$; (iii) $c \ge s, k < s$; and (iv) $c\ge s, k\ge s$.

At optimality, it can be shown that

$$\begin{aligned} P(X_{ij} = k|Y_j = c) = \exp [\sigma _i(c,k) + \tau _j(c,k)]/ Z_{ijc}, \end{aligned}$$

(3)

where $Z_{ijc}$ is a normalization factor,

$$\begin{aligned} \sigma _i(c,k)= & {} \sum _{1\le s\le m}\!\sum _{\vartriangle ,\triangledown }\sigma _{is}^{\vartriangle ,\triangledown }\mathbb {I}(c\vartriangle s, k\triangledown s), \end{aligned}$$

(4)

$$\begin{aligned} \tau _j(c,k)= & {} \sum _{1\le s\le m}\!\sum _{\vartriangle ,\triangledown }\tau _{js}^{\vartriangle ,\triangledown }\mathbb {I}(c\vartriangle s, k\triangledown s), \end{aligned}$$

(5)

$\sigma _{is}^{\vartriangle ,\triangledown }$, $\tau _{js}^{\vartriangle ,\triangledown }$ are Lagrange multipliers for the constraints (1) and (2), respectively, and $\mathbb {I}(\cdot )$ is the indicator function. Note that $\sigma _i(c,k)$ controls how likely worker i assigns label k when the true label is c, and ${\tau }_j(c,k)$ controls how likely item j is assigned label k when the true label is c. Equations (4) and (5) can be written more compactly as $\sigma _i(c,k) = \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\sigma }}_i$ and $\tau _j(c,k) = \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\tau }}_j,$ where $\varvec{\mathbf {\sigma }}_i=[\sigma _{is}^{\vartriangle , \triangledown }]$, $\varvec{\mathbf {\tau }}_j=[\tau _{js}^{\vartriangle , \triangledown }]$, and $\varvec{\mathbf {t}}_{ck}=[\mathbb {I}(c{\vartriangle }s, k{\triangledown }s)]$. Moreover, let $\varvec{\mathbf {X}}= [X_{ij}]_{(i,j)\in \varXi }$, and $\varvec{\mathbf {Y}}= [Y_j]$. Equation (3) can be rewritten as

$$\begin{aligned} P(\varvec{\mathbf {X}}| \varvec{\mathbf {Y}})= & {} \prod _{(i,j)\in \varXi }\prod _{c,k} P(X_{ij} = k| Y_j = c)^{\mathbb {I}(X_{ij} = k, Y_j = c)} \nonumber \\= & {} \prod _{(i,j)\in \varXi }\prod _{c,k} \left[ \frac{1}{Z_{ijc}}\exp [\varvec{\mathbf {t}}^T_{ck}(\varvec{\mathbf {\sigma }}_i + \varvec{\mathbf {\tau }}_j) ]\right] ^{\mathbb {I}(X_{ij}=k ,Y_j = c)}. \end{aligned}$$

(6)

3 Bayesian Clustering of Workers and Items

Note that each worker i (resp. item j) has its own set of variables $\{\sigma _i(c,k)\}$ (resp. $\{\tau _j(c,k)\}$). When the data are sparse, i.e., the set $\varXi$ of observed labels is small, an accurate estimation of these variables can be difficult. In this section, we alleviate this data sparsity problem by clustering workers and items. While the minimax optimization framework in [26] can utilize ordering information in the ordinal labels, it is non-Bayesian and clustering cannot be easily encouraged. In this paper, we propose a full Bayesian model, and encourage clustering of workers and items using the Dirichlet process (DP) [9]. The DP prior is advantageous in that the number of clusters does not need to be specified in advance. However, with the non-conjugate priors and DPs involved, inference of the proposed model becomes more difficult. By extending the work in [11], we derive a variational Bayesian inference algorithm to infer the parameters and aggregate labels.

3.1 Model

Recall that $\sigma _i(c,k) = \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\sigma }}_i$ controls how likely worker i assigns label k when the true label is c. To encourage worker clustering, we define a prior $G_a$ on $\{\varvec{\mathbf {\sigma }}_i\}_{i=1}^N$. $G_a$ is drawn from the Dirichlet process $\text {DP}(\beta _a, G_{a0})$, where $\beta _a$ is the concentration parameter, and $G_{a0}$ is the base distribution (here, we use the normal distribution $\mathcal {N}(\varvec{\mathbf {\mu }}_0, \varvec{\mathbf {\Sigma }}_0)$). Similarly, as ${\tau }_j(c,k) = \varvec{\mathbf {t}}^T_{ck}\varvec{\mathbf {\tau }}_j$ controls how likely item j assigns label k when the true label is c, we define a prior $G_b \sim \text {DP}(\beta _b, G_{b0})$ on $\{\varvec{\mathbf {\tau }}_j\}_{j=1}^M$ to encourage item clustering (with $G_{b0}= \mathcal {N}(\varvec{\mathbf {\nu }}_0, \varvec{\mathbf {\Omega }}_0)$).

To make variational inference possible, we use the stick-breaking representation [20] and rewrite $G_a$ as $\sum ^{\infty }_{l=1}\phi _l \delta _{\varvec{\mathbf {\sigma }}_l^*}$, where $\phi _l = V_l\prod ^{l-1}_{d=1}(1-V_d), V_l \sim \text {Beta}(1,\beta _a)$, and $\varvec{\mathbf {\sigma }}_l^* \sim G_{a0}$. When we draw $\varvec{\mathbf {\sigma }}$ from $G_a$, $\delta _{\varvec{\mathbf {\sigma }}_l^*} = 1$ if $\varvec{\mathbf {\sigma }}= \varvec{\mathbf {\sigma }}_l^*$, and 0 otherwise. Similarly, $G_b = \sum ^{\infty }_{i=1}\varphi _h \delta _{\varvec{\mathbf {\tau }}_h^*}$, where $\varphi _h = H_h\prod ^{h-1}_{d=1}(1-H_d)$, $H_h \sim \text {Beta}(1,\beta _b)$ and $\varvec{\mathbf {\tau }}_h^* \sim G_{b0}$. Similar to $\sigma _i(c,k), \tau _j(c,k)$ in [26], $\sigma ^*_l(c,k) = \varvec{\mathbf {t}}^T_{ck}\varvec{\mathbf {\sigma }}^*_l$ controls how likely workers in cluster l assign label k when the true label is c, and $\tau ^*_h(c,k) = \varvec{\mathbf {t}}^T_{ck}\varvec{\mathbf {\sigma }}^*_h$ controls how likely items in cluster h are assigned label k when the true label is c Let $z_i$ (resp. $u_j$) indicate the cluster that worker i (resp. item j) belongs to. We then have $\sigma _i(c,k) = \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\sigma }}^*_{z_i}$ and $\tau _j(c,k) = \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\tau }}^*_{u_j}$ for all i, j, c, k. Putting these into (6), we obtain the conditional probability as

$$\begin{aligned} P(\varvec{\mathbf {X}}| \varvec{\mathbf {Y}}, \varvec{\mathbf {z}}, \varvec{\mathbf {u}}, \varvec{\mathbf {\sigma }}^*, \varvec{\mathbf {\tau }}^*) = \prod _{(i,j)\in \varXi } \prod _{c,k} \left[ \frac{1}{Z_{ijc}}\exp \left[ \varvec{\mathbf {t}}^T_{ck}(\varvec{\mathbf {\sigma }}_{z_i}^* + \varvec{\mathbf {\tau }}_{u_j}^*)\right] \right] ^{\mathbb {I}(X_{ij}=k ,Y_j = c)}, \end{aligned}$$

(7)

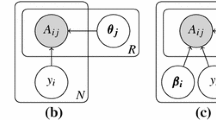
where $Z_{ijc} = \sum _k\exp [\varvec{\mathbf {t}}_{ck}^T(\varvec{\mathbf {\sigma }}^*_{z_i} +\varvec{\mathbf {\tau }}^*_{u_j})]$, $\varvec{\mathbf {\sigma }}^* = [\varvec{\mathbf {\sigma }}^*_l], \varvec{\mathbf {\tau }}^* = [\varvec{\mathbf {\tau }}^*_h], \varvec{\mathbf {z}}= [z_i]$, and $\varvec{\mathbf {u}}= [u_j]$. In other words, rating $X_{ij}$ is generated from a softmax function [3] conditioned on $Y_j, z_i, u_j, \varvec{\mathbf {\sigma }}^*, \varvec{\mathbf {\tau }}^*$. Finally, the true label $Y_j$ of item j is drawn from the multinomial distribution $\text {Mult}(\pi _1,\pi _2,\dots , \pi _m)$, where $\pi _1, \dots , \pi _m$ are drawn from a Dirichlet prior with hyperparameter $\alpha$. The whole label generation process is shown in Algorithm 1. A graphical representation of the Bayesian model, which will be called Cluster-based Ordinal Label Aggregation (COLA) in the sequel, is shown in Fig. 1.

Fig. 1.

Graphical representation of the proposed model.

3.2 Inference Procedure

The joint distribution can be written as

where $\varvec{\mathbf {V}}= [V_l]$, and $\varvec{\mathbf {H}}=[H_h]$. Monte Carlo Markov Chain (MCMC) sampling [1] can be used to approximate the posterior distribution. However, it can be slow and its convergence is difficult to diagnose [4]. Another approach is variational inference [11], which approximates the posterior distribution by maximizes a lower bound of the marginal likelihood. However, due to the infinite number of variables in the DPs and our use of non-conjugate priors, standard variational inference cannot be used. To solve this problem, we propose an integration of the techniques in [4, 5] with variational inference. Specifically, we infer the variational parameters of the DPs based on an extension of [4], and handle the non-conjugate priors by a technique similar to [5].

Let $\varvec{\mathbf {\theta }}= \{\varvec{\mathbf {\sigma }}^*, \varvec{\mathbf {\tau }}^*, \varvec{\mathbf {Y}}, \varvec{\mathbf {\pi }}, \varvec{\mathbf {z}}, \varvec{\mathbf {u}}, \varvec{\mathbf {V}}, \varvec{\mathbf {H}}\}$. In variational inference, the posterior $P(\varvec{\mathbf {\theta }}|\varvec{\mathbf {X}})$ is approximated by a distribution $q(\varvec{\mathbf {\theta }})$. The log likelihood of the marginal distribution of $\varvec{\mathbf {X}}$ is $\log {P(\varvec{\mathbf {X}})}= \mathcal {L}(q) + \text {KL}(q\Vert P_{\varvec{\mathbf {\theta }}|\varvec{\mathbf {X}}})$, where $\mathcal {L}(q) = \int {q(\varvec{\mathbf {\theta }})\log \frac{P(\varvec{\mathbf {X}}, \varvec{\mathbf {\theta }})}{q(\varvec{\mathbf {\theta }})}\text {d}\varvec{\mathbf {\theta }}}$, and $\text {KL}(q\Vert P_{\varvec{\mathbf {\theta }}|\varvec{\mathbf {X}}} ) = \int {q(\varvec{\mathbf {\theta }})\log \frac{q(\varvec{\mathbf {\theta }})}{P(\varvec{\mathbf {\theta }}| \varvec{\mathbf {X}})} \text {d}\varvec{\mathbf {\theta }}}$ is the KL divergence between q and $P_{\varvec{\mathbf {\theta }}|\varvec{\mathbf {X}}}$. As $\text {KL}(q\Vert P_{\varvec{\mathbf {\theta }}|\varvec{\mathbf {X}}})\ge 0$, we simply maximize the lower bound $\mathcal {L}(q)$ of $\log {P(\varvec{\mathbf {X}})}$. Using the variational mean field approach, $q(\varvec{\mathbf {\theta }})$ is assumed to be factorized as $\prod _{n=1}^S q_n(\varvec{\mathbf {\theta }}_n)$, where S is the number of factors, $\{\varvec{\mathbf {\theta }}_1, \dots , \varvec{\mathbf {\theta }}_S\}$ is a partition of $\varvec{\mathbf {\theta }}$, and $q_n$ is the variational distribution of $\varvec{\mathbf {\theta }}_n$ [22]. We perform alternating maximization of $\mathcal {L}\left( \prod _{n=1}^Sq_n(\varvec{\mathbf {\theta }}_n)\right)$ w.r.t. $q_n$’s. It can be shown that the optimal $q_n$ is given by

$$\begin{aligned} q_n^*(\varvec{\mathbf {\theta }}_n) = \exp \left[ \mathbb {E}_{q(\varvec{\mathbf {\theta }}_{\lnot {n}})} \log P(\varvec{\mathbf {X}}, \varvec{\mathbf {\theta }}) \right] + \text {constant}, \end{aligned}$$

(8)

where $\varvec{\mathbf {\theta }}_{\lnot n}$ is the subset of variables in $\varvec{\mathbf {\theta }}$ excluding $\varvec{\mathbf {\theta }}_n$, and $\mathbb {E}_{q(\varvec{\mathbf {\theta }}_{\lnot {n}})}$ is the corresponding expectation operator.

As there are infinite variables in the stick-breaking representations of $\text {DP}(\beta _a, G_{a0})$ and $\text {DP}(\beta _b, G_{b0})$, we set a maximum on the numbers of clusters as in [4]. Note that the exact distributions of the stick-breaking process are not truncated. The factorized variational distribution is

where $K_1, K_2$ are the truncated numbers of clusters for workers and items, respectively. Using (8), it can be shown that the variational distributions of $\{\varvec{\mathbf {Y}}, \varvec{\mathbf {\pi }}, \varvec{\mathbf {z}}, \varvec{\mathbf {u}}, \varvec{\mathbf {H}}, \varvec{\mathbf {V}}\}$ can be easily obtained as:

$$\begin{aligned} q^*_{Y_j}(Y_j) = \text {Mult}(\varvec{\mathbf {r}}^Y_{j}),&q^*_{\varvec{\mathbf {\pi }}}(\varvec{\mathbf {\pi }}) = \text {Dir}(\alpha _1,\alpha _2,\dots \alpha _m), \\ q^*_{z_i}(z_i) = \text {Mult}(\varvec{\mathbf {r}}^z_{i}),&q^*_{u_j}(u_j) = \text {Mult}(\varvec{\mathbf {r}}^u_{j}), \\ q^*_{V_l}(V_l) = \text {Beta}(\gamma _{l,1}, \gamma _{l,2}),&q^*_{H_h}(H_h) = \text {Beta}(\eta _{h,1}, \eta _{h,2}), \end{aligned}$$

where $\{\varvec{\mathbf {r}}^Y_{j}\}_{j=1}^M, \{\varvec{\mathbf {r}}^z_i\}_{i=1}^N, \{\varvec{\mathbf {r}}^u_j\}_{j=1}^M, \{\alpha _c\}_{c=1}^m, \{\gamma _{l, 1}, \gamma _{l,2}\}_{l=1}^{K_1}$, and $\{\eta _{h,1}, \eta _{h,2}\}_{h=1}^{K_2}$ are variational parameters. All these have closed-form updates as

$$ r^{Y}_{jc} \leftarrow \frac{1}{Z^Y_j}\exp \left[ \mathbb {E}_{q(\varvec{\mathbf {\theta }}_{\lnot \varvec{\mathbf {Y}}})}\log \pi _c +\sum _{i:(i,j) \in \varXi }^N\sum _{l=1}^{K_1}\sum _{h=1}^{K_2} r^z_{il} r^u_{jh}U_{ijlhc} \right] , $$

$$ r^z_{il} \leftarrow \frac{1}{Z^z_{i}} \exp \left[ \mathbb {E}_{q(\varvec{\mathbf {\theta }}_{\lnot \varvec{\mathbf {z}}})} \log \phi _l+ \sum _{j:(i,j)\in \varXi } \sum _{c=1}^{m}\sum _{h=1}^{K_2} r^u_{jh} r_{jc}^YU_{ijlhc}\right] , $$

$$ r_{jh}^u \leftarrow \frac{1}{Z^u_{j}}\exp \left[ \mathbb {E}_{q(\varvec{\mathbf {\theta }}_{\lnot \varvec{\mathbf {u}}})}\log \varphi _h + \sum _{i:(i,j)\in \varXi } \sum _{c=1}^{m}\sum _{l=1}^{K_1} r_{il}^z r_{jc}^YU_{ijlhc}\right] , $$

$$ \alpha _c \leftarrow \frac{\alpha }{m} + \sum _{j=1}^{M} r^Y_{jc},~~ \gamma _{l,1} \leftarrow 1 + \sum _{i=1}^N r_{il}^z,~~ \gamma _{l,2} \leftarrow \beta _a + \sum _{i=1}^N \sum _{d = l+1}^{K_1}r_{id}^z, $$

$$ \eta _{h,1} \leftarrow 1 + \sum _{j=1}^M r_{jh}^u,~~ \eta _{h,2} \leftarrow \beta _b + \sum _{j=1}^M \sum _{d = h+1}^{K_2}r_{jd}^u, $$

where $Z_j^Y, Z_i^z, Z_j^u$ are normalization constants,

$$\begin{aligned} U_{ijlhc} = \sum _{k=1}^mI(X_{ij}=k) \varvec{\mathbf {t}}_{ck}^T [\mathbb {E}_{q(\varvec{\mathbf {\sigma }}^*_l)}(\varvec{\mathbf {\sigma }}^*_l)+\mathbb {E}_{q(\varvec{\mathbf {\tau }}^*_h)}(\varvec{\mathbf {\tau }}^*_h)] - \mathbb {E}_{q(\varvec{\mathbf {\sigma }}^*_l,\varvec{\mathbf {\tau }}^*_h)} Z_{lhc}^* \end{aligned}$$

(9)

and $Z^*_{lhc} = \sum _{k=1}^m\exp [\varvec{\mathbf {t}}_{ck}^T(\varvec{\mathbf {\sigma }}^*_{l} +\varvec{\mathbf {\tau }}^*_{h})]$. Computing $U_{ijlhc}$ requires knowing the variational distributions of $\varvec{\mathbf {\sigma }}^*_l$ and $\varvec{\mathbf {\tau }}^*_h$, and will be derived in the following.

Recall that $P(\varvec{\mathbf {\sigma }}_l^*), P(\varvec{\mathbf {\tau }}_h^*)$ are normal distributions. These are not the conjugate prior of $P(\varvec{\mathbf {X}}|\varvec{\mathbf {Y}}, \varvec{\mathbf {z}},\varvec{\mathbf {u}}, \varvec{\mathbf {\sigma }}^*, \varvec{\mathbf {\tau }}^*)$ in (7). Thus, on maximizing $\mathcal {L}$, $q(\varvec{\mathbf {\sigma }}^*)$ and $q(\varvec{\mathbf {\tau }}^*)$ do not have closed-form solutions. Note that the $\frac{1}{Z_{ijc}}\exp \left[ \varvec{\mathbf {t}}_{ck}^T(\varvec{\mathbf {\sigma }}_{z_i}^* + \varvec{\mathbf {\tau }}_{u_j}^*)\right]$ term in (7) is a softmax function similar to that in [5], which uses variational inference to learn discrete choice models. However, while the parameters of different sets of choices in [5] are conditionally independent, here in (7) they are coupled together. Thus, the inference procedure in [5] cannot be directly applied and has to be extended.

First, (7) can be rewritten as

$$ P(\varvec{\mathbf {X}}| \varvec{\mathbf {Y}}, \varvec{\mathbf {z}}, \varvec{\mathbf {u}},\varvec{\mathbf {\sigma }}^*,\varvec{\mathbf {\tau }}^*)\,=\, \prod _{(i,j) \in \varXi }\prod _{c,k,l,h} \!\!\! \left[ \frac{\exp \left[ \varvec{\mathbf {t}}^T_{ck}(\varvec{\mathbf {\sigma }}_l^* + \varvec{\mathbf {\tau }}_h^*)\right] }{Z^*_{lhc}} \right] ^{\mathbb {I}(z_i=l, u_j =h,X_{ij}=k ,Y_j = c)}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!. $$

Since $P(\varvec{\mathbf {\sigma }}_l^*), P(\varvec{\mathbf {\tau }}_h^*)$ are normal distributions, we constrain the variational distributions of $\varvec{\mathbf {\sigma }}_l^*$ and $\varvec{\mathbf {\tau }}_h^*$ to be also normal, i.e., $q_{\varvec{\mathbf {\sigma }}^*_l}(\varvec{\mathbf {\sigma }}^*_l) = \mathcal {N}(\varvec{\mathbf {\mu }}_l, \varvec{\mathbf {\Sigma }}_l)$, and $q_{\varvec{\mathbf {\tau }}^*_h}(\varvec{\mathbf {\tau }}^*_h) = \mathcal {N}(\varvec{\mathbf {\nu }}_h, \varvec{\mathbf {\Omega }}_h)$. Let $\varvec{\mathbf {\mu }}= [\varvec{\mathbf {\mu }}_l]$, $\varvec{\mathbf {\nu }}= [\varvec{\mathbf {\nu }}_h]$, $\varvec{\mathbf {\Sigma }}= [\varvec{\mathbf {\Sigma }}_l]$, and $\varvec{\mathbf {\Omega }}= [\varvec{\mathbf {\Omega }}_h]$. On maximizing $\mathcal {L}(q)$, it can be shown that the variational parameters $\{\varvec{\mathbf {\mu }}, \varvec{\mathbf {\Sigma }}, \varvec{\mathbf {\nu }}, \varvec{\mathbf {\Omega }}\}$ can be obtained as

(10)

The first term is the entropy of the normal distribution, and the second term is the cross-entropy of two normal distributions. Both are easy to compute. The last term can be rewritten as $\sum _{(i,j) \in \varXi }\sum _{c,k,l,h}r_{il}^zr_{jh}^ur_{jc}^Y\mathbb {I}(X_{ij}=k) \left( \varvec{\mathbf {t}}^T_{ck}(\varvec{\mathbf {\mu }}_l + \varvec{\mathbf {\nu }}_h) -\mathbb {E}_{q(\varvec{\mathbf {\sigma }}^*, \varvec{\mathbf {\tau }}^*)}\log Z^*_{lhc} \right)$. The term $\mathbb {E}_{q(\varvec{\mathbf {\sigma }}^*, \varvec{\mathbf {\tau }}^*)}\log Z^*_{lhc}$, which also appears in (9), can be approximated as in [5]:

$$\log \sum _{k=1}^m\exp (\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\mu }}_l + \frac{1}{2} \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\Sigma }}_l \varvec{\mathbf {t}}_{ck}) \exp (\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\nu }}_h + \frac{1}{2} \varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\Omega }}_h \varvec{\mathbf {t}}_{ck}). $$

Problem (10) can then be solved via gradient-based methods, such as L-BFGS [17]. Denote the objective by f. It can be shown that

$$\begin{aligned} \begin{aligned} \frac{\partial f}{\partial \varvec{\mathbf {\mu }}_l}&= -\varvec{\mathbf {\Sigma }}_0^{-1} (\varvec{\mathbf {\mu }}_l - \varvec{\mathbf {\mu }}_0) + \sum _{(i,j) \in \varXi }\sum _{c=1}^m\sum _{h=1}^{K_2}r^z_{il}r^u_{jh} r^Y_{jc} \sum _{k=1}^m[\mathbb {I}(X_{ij} = k) - w_{klh} ]\varvec{\mathbf {t}}_{ck}, \end{aligned} \end{aligned}$$

where

$$ w_{klh} = \frac{\exp (\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\nu }}_h + \frac{1}{2}\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\Omega }}_h \varvec{\mathbf {t}}_{ck})\exp (\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\mu }}_l + \frac{1}{2}\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\Sigma }}_l\varvec{\mathbf {t}}_{ck})}{\sum _{k=1}^m\exp (\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\nu }}_h + \frac{1}{2}\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\Omega }}_h \varvec{\mathbf {t}}_{ck})\exp (\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\mu }}_l + \frac{1}{2}\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {\Sigma }}_l \varvec{\mathbf {t}}_{ck})}. $$

Moreover, as $\varvec{\mathbf {\Sigma }}_l \succeq 0$, we assume that $\varvec{\mathbf {\Sigma }}_l = \varvec{\mathbf {L}}_l^T \varvec{\mathbf {L}}_l$, where $\varvec{\mathbf {L}}_l$ is lower-triangular. It can then be shown that

$$\begin{aligned} \frac{\partial f}{\partial \varvec{\mathbf {L}}_l} = \varvec{\mathbf {L}}_l^{-T} -\left[ \varvec{\mathbf {\Sigma }}_0^{-1} - \sum _{(i,j)\in \varXi }\sum _{c=1}^m\sum _{h=1}^{K_2} r^z_{il}r^u_{jh} r^Y_{jc} \left( \sum _{k=1}^mw_{klh}\varvec{\mathbf {t}}_{ck}^T\varvec{\mathbf {t}}_{ck}\right) \right] \varvec{\mathbf {L}}_l. \end{aligned}$$

Recall that $\varvec{\mathbf {L}}_l$ is lower-triangular, so in updating $\varvec{\mathbf {L}}_l$, we only need the diagonal elements $(\varvec{\mathbf {L}}_l^{-T})_{ii} = 1/(\varvec{\mathbf {L}}_l)_{ii}$. of the upper-triangular $\varvec{\mathbf {L}}_l^{-T}$ [5]. The gradients of f w.r.t. $\varvec{\mathbf {\nu }}$ and $\varvec{\mathbf {\Omega }}$ can be obtained in a similar manner.

4 Experiments

4.1 Synthetic Data Set

In this section, we perform experiments on synthetic data. Workers are generated from three clusters (w1, w2, w3), items from three clusters (i1, i2, i3), and ordinal labels in $\{1,2,3,4,5\}$. The cluster parameters $\varvec{\mathbf {\sigma }}^*,\varvec{\mathbf {\tau }}^*$ are sampled independently from the normal distribution with means in Table 1 and standard deviation 0.1. Confusion matrices¹ of the clusters are shown in Fig. 2. As can be seen, workers in cluster w1 are the least confused in label assignment. This is followed by cluster w2, and workers in cluster w3 are most confused (spammers). Similarly, items in cluster i1 are the least confused, while those in i3 are the most confused.

Table 1. Parameter means of the worker clusters (w1, w2, w3) and item clusters (i1, i2, i3).

Fig. 2.

True confusion matrices of the worker and item clusters.

We generate two data sets. Both have 300 workers from the 3 clusters (w1, w2, w3), with sizes 200, 50, and 50, respectively. The first data set (D1) has 1200 items coming from the 3 clusters (i1, i2, i3), with sizes 800, 200, and 200, respectively. Each item is labeled by 6 randomly selected workers. The second data set (D2) has 300 items coming from the 3 clusters with sizes 200, 50, and 50, respectively. Each item is labeled by 30 workers.

We set the truncated numbers of clusters $K_1, K_2$ in COLA to 8, and $\varvec{\mathbf {\mu }}_0 = \mathbf{0}, \varvec{\mathbf {\nu }}_0 = \mathbf{0}$, $\varvec{\mathbf {\Sigma }}_0 = \frac{1}{\lambda _a}\mathbf{I}, \varvec{\mathbf {\Omega }}_0 = \frac{1}{\lambda _b}\mathbf{I}$, where $\lambda _b = \lambda _a M/N$, as in [26]. Parameters $\beta _a, \beta _b, \alpha$ and $\lambda _a$ are tuned by maximizing the log-likelihood as in [26]. Latent variables are initialized in an non-informative manner: $\varvec{\mathbf {\mu }}_l = \mathbf{0}, \varvec{\mathbf {\nu }}_h = \mathbf{0}$, $\varvec{\mathbf {r}}^z_{i} = [1/K_1,\dots ,1/K_1]^T$, $\varvec{\mathbf {r}}^u_{j} = [1/K_2,\dots ,1/K_2]^T$, $\eta _{h,1} = 1, \eta _{h,2} = \beta _a$ $\gamma _{l,1} = 1, \gamma _{l,2} = \beta _b$, and $\varvec{\mathbf {r}}^Y_j$ is from the empirical probabilities of the observed labels. We compare the proposed algorithm with the following state-of-the-art:

• 1. Ordinal minimax entropy (OME) [26], with the hyperparameters tuned by the cross-validation method suggested in [26].

• 2. Ordinal mixture (ORDMIX) [16]: The predicted labels are obtained by discretizing (normally distributed) continuous-valued latent labels.

• 3. Dawid-Skene model (DS) [7]: A well-known approach for label aggregation, which estimates a confusion matrix for each worker.

• 4. Majority voting (MV) [14], which has been commonly used as a simple baseline.

To allow statistical significance testing, we learn the model using $90\,\%$ of the items and run each experiment for 10 repetitions. As in [16, 26], the following measures are used: (i) mean squared error: $\text {MSE} = \frac{1}{|S|} \sum _{j\in S}((\mathbb {E}_{Q}[Y_j] - Y^*_j)^2)$, where S is the set of items with ground-truth labels $Y^*_j$’s; (ii) $\ell _0$ error $= \frac{1}{|S|} \sum _{j\in S}\mathbb {E}_{Q}[\mathbb {I}(Y_j \ne Y^*_j)]$; (iii) $\ell _1$ error $= \frac{1}{|S|} \sum _{j\in S}\mathbb {E}_Q[|Y_j - Y^*_j|]$; and (iv) $\ell _2$ error $= \sqrt{\frac{1}{|S|} \sum _{j\in S}\mathbb {E}_{Q}[(Y_j - Y^*_j)^2] }$.

Results are shown in Table 2. As can be seen, on data set D1, the proposed COLA significantly outperforms the other methods. On D2, with more labels per item, inference becomes easier and all methods have improved performance. COLA is still better in terms of MSE and $\ell _2$ error, but can be slightly outperformed by the simpler methods of DS and MV in terms of $\ell _0$ and $\ell _1$ errors.

Table 2. Errors obtained on the synthetic data sets. The best results and those that are not statistically worse (using paired t-test at 95 % significance level) are in bold.

Figure 3 shows the normalized sizes of the worker and item clusters obtained by COLA. Recall that $\varvec{\mathbf {z}}$ indicates the cluster memberships of workers. The normalized size of worker cluster l is defined as $\mathbb {E}(S^z_l)/\sum _{l=1}^{K_1}\mathbb {E}(S^z_l)$, where $S^z_l$ is the size of worker cluster l, and $\mathbb {E}(S^z_l) =\mathbb {E}\left[ \sum _{i=1}^N I(z_i=l) \right] = \sum _{i=1}^N P(z_i=l) = \sum _{i=1}^N r^z_{il}$. Similarly, the normalized size of item cluster h is $\mathbb {E}(S^u_h)/\sum _{h=1}^{K_2}\mathbb {E}(S^u_h)$, where $S^u_h$ is the size of item cluster h, and $\mathbb {E}(S^u_h) =\sum _{j=1}^M r^u_{jh}$. As can be seen, the sizes of the three dominant worker clusters are close to the ground truth on both data sets. However, the item cluster (normalized) sizes on D1 are less accurate than those on D2. This is due to that each item in D1 only has 6 labels, while each item in D2 has 30 (in comparison, each worker on average has 24 labels for D1 and 30 labels for D2).

Fig. 3.

Normalized sizes of the worker and item clusters on D1 (left) and D2 (right). The true normalized sizes of the worker and item clusters are 0.667,0.167,0.167.

Next, we show the confusion matrices of the obtained clusters. Since we only have the distributions of $\varvec{\mathbf {\sigma }}^*$ and $\varvec{\mathbf {\tau }}^*$, we will use their expectations. Note that $\mathbb {E}[\varvec{\mathbf {\sigma }}_l^*] = \varvec{\mathbf {\mu }}_l$. From (7), the (c, k)th entry of the confusion matrix of worker cluster l can be represented as $\exp [\varvec{\mathbf {t}}^\top _{ck}\varvec{\mathbf {\mu }}_l]/\sum _k \exp [\varvec{\mathbf {t}}^\top _{ck}\varvec{\mathbf {\mu }}_l]$, and similarly, that of the item cluster h is $\exp [\varvec{\mathbf {t}}^\top _{ck}\varvec{\mathbf {\nu }}_h]/\sum _k \exp [\varvec{\mathbf {t}}^\top _{ck}\varvec{\mathbf {\nu }}_h]$. The obtained confusion matrices for worker and item clusters are shown in Fig. 4. Here, we focus on the three largest worker/item clusters, which can be seen to dominate in Fig. 3. Comparing with the ground-truth in Fig. 2, the 3 worker and item clusters can be well detected. Note again that the item clusters obtained on D2 are more accurate than those on D1, as each item in D2 has more labels for inference.

Fig. 4.

Confusion matrices of the obtained worker/item clusters on D1 (top) and D2 (bottom).

4.2 Real Data Sets

In this section, experiments are performed on three commonly-used data sets (Table 3).

• 1. AC2 [10]: This contains AMT judgments for website ratings, with the 4 levels: “G”, “PG”, “R”, and “X”;

• 2. TREC [6]: This is a web search data set, with the 3 levels: “NR” (non-relevant), “R” (relevant) and “HR” (highly relevant);

• 3. WEB [26]: This is another web search relevance data set, with the 5 levels: “P” (perfect), “E” (excellent), “G” (good), “F” (fair) and “B” (bad).

The ordinal labels are converted to numbers (e.g., on the AC2 data set, “G”, “PG”, “R”, and “X” are converted to 1, 2, 3, 4, respectively). As can be seen from Table 3, the number of labels provided by the workers can vary significantly.

Table 3. Summary of the data sets used.

For the proposed algorithm, we set the truncated numbers of clusters $K_1, K_2$ to 10 (on WEB, $K_1 = 15$). Larger values do not improve performance. The other parameters of all the algorithms are set as in Sect. 4.1. To allow statistical significance testing, again we learn the model using $90\,\%$ of the items², and repeat this process 10 times.

Results are shown in Table 4. As can be seen, COLA consistently outperforms all the other methods on AC2 and WEB. Moreover, ORDMIX is competitive with COLA on TREC, but much inferior on AC2 and WEB. As AC2 and WEB have more label classes than TREC (Table 3), ORDMIX, which has fewer parameters and is less flexible than COLA, is unable to sufficiently model the confusion matrices of workers and items. The performance of DS is also poor, as ordinal information of the labels is not utilized. Finally, as expected, the simple MV performs the worst overall.

Table 4. Errors obtained on the real-world data sets. The best results and those that are not statistically worse (using paired t-test at 95 % significance level) are in bold.

Figure 5(a)–(j) show the confusion matrices of worker clusters obtained on AC2. For most of them ($\widehat{w1}-\widehat{w8}$), the diagonal values for “G” and “X” are high, indicating that most clusters can identify these two types of websites easily. For the largest worker cluster ($\widehat{w1}$), the highest value on each row lies on the diagonal, and so the labels assigned by this cluster are mostly consistent with the ground truth. As for cluster $\widehat{w5}$, the diagonal entries are much larger than the non-diagonal ones. Hence, the worker labels are often the same as the ground truth, suggesting that these workers are experts. This is also confirmed in Table 5, which shows the $\ell _2$ error for each cluster. On the other hand, workers in cluster $\widehat{w9}$ almost always predict “G”. They are likely to be spammers as observed in many crowdsourcing platforms [18]. In cluster $\widehat{w10}$, the off-diagonal values are larger than the diagonal ones, indicating that workers in this cluster may not understand this website rating task or may even be malicious.

Fig. 5.

Confusion matrices for worker clusters (top two rows) and item clusters (bottom row) obtained by COLA on the AC2 data set (clusters are ordered by decreasing size). In each cluster, columns are the cluster-assigned labels (left-to-right: “G”, “PG”, “R”, “X”), and rows are the true labels (top-to-down: “G”, “PG”, “R”, “X”). The five smallest item clusters occupy less than $2\,\%$ of the total size, and so are not shown.

Table 5. $\ell _2$ errors for worker clusters obtained on the AC2 data set.

Figure 5(k)–(o) show the confusion matrices of the obtained item clusters. In general, as each item has fewer labels than each worker, the clustering structure here is less obvious (as discussed in Sect. 4.1). For the item cluster $\widehat{i1}$, the diagnal elements have high values, indicating that items belonging to this cluster are relatively easy to distinguish. Item cluster $\widehat{i2}$ tends to assign label “G” more often. In $\widehat{i3}$, “G” and “PG” are sometimes confused, and so are “R” and “X”.

Varying the Number of Items. In this experiment, we use item subsets of different sizes to learn the model. With a smaller number of items, the number of labels per worker is also reduced (Fig. 6), and estimating the workers’ behavior become more difficult. Here, we focus on the two top performers in Table 4, namely, COLA and OME. Figure 7(a)–(i) show the errors averaged over 10 repetitions. As can be seen, as OME does not consider any structure among workers and items, its performance deteriorates significantly with fewer worker labels. On the other hand, COLA clusters workers and items. Thus, information within a cluster can be shared, and the performance is less affected.

Fig. 6.

Number of labels per worker with different numbers of items.

Fig. 7.

$\ell _0$, $\ell _1$ and $\ell _2$ errors for COLA and OME with different proportions($\%$) of items used.

Varying the Concentration Parameters. In this experiment, we study the effect of the DP’s concentration parameters on the performance of COLA. In general, a smaller concentration parameter encourages fewer clusters, and vice verse. We first fix $\beta _b$ to the value obtained in the previous experiment, and vary $\beta _a$ from 0.1 to 3.5.

Fig. 8.

$\ell _2$ errors of COLA on the AC2 data set, with different values for $\beta _a, \beta _b$.

Figure 8(a) shows how the $\ell _2$ error varies with $\beta _a$. Because of the lack of space, we only show results on the AC2 data set. COLA has stable performance over a wide range of $\beta _a$. When $\beta _a$ becomes too small, workers can only form very few clusters, and each cluster may not be coherent. When $\beta _a$ is too large, clusters are split, and each cluster may not have enough data for accurate parameter estimation. Figure 8(b) shows the results on varying $\beta _b$. As can be seen, $\beta _b$ has little influence on the performance. Again, this is consistent with the observation in the previous section that items’ cluster structure is more difficult to identify.

5 Conclusion

In this paper, we proposed a Bayesian clustering model to aggregate crowdsourced ordinal labels. Using the Dirichlet process, we encourage the formation of worker and item clusters in the label generating process, which leads to more accurate label estimation. While the probability model is complex and uses non-conjugate DPs, we derive an efficient variational inference procedure to infer the posterior distributions. Experimental results show that the proposed method yields significantly better accuracy than the state-of-the-art, and is more robust to sparser labels. Moreover, it detects meaningful clusters, which can help the user to study the group’s behavior.