Single Image Dehazing via Multi-scale Convolutional Neural Networks

Abstract

The performance of existing image dehazing methods is limited by hand-designed features, such as the dark channel, color disparity and maximum contrast, with complex fusion schemes. In this paper, we propose a multi-scale deep neural network for single-image dehazing by learning the mapping between hazy images and their corresponding transmission maps. The proposed algorithm consists of a coarse-scale net which predicts a holistic transmission map based on the entire image, and a fine-scale net which refines results locally. To train the multi-scale deep network, we synthesize a dataset comprised of hazy images and corresponding transmission maps based on the NYU Depth dataset. Extensive experiments demonstrate that the proposed algorithm performs favorably against the state-of-the-art methods on both synthetic and real-world images in terms of quality and speed.

1 Introduction

Image dehazing, which aims to recover a clear image from one single noisy frame caused by haze, fog or smoke, as shown in Fig. 1, is a classical problem in computer vision. The formulation of a hazy image can be modeled as

$$\begin{aligned} \varvec{I}(x)=\varvec{J}(x)t(x)+\varvec{A}(1-t(x)), \end{aligned}$$

(1)

where $\varvec{I}(x)$ and $\varvec{J}(x)$ are the observed hazy image and the clear scene radiance, $\varvec{A}$ is the global atmospheric light, and t(x) is the scene transmission describing the portion of light that is not scattered and reaches the camera sensors. Assuming that the haze is homogenous, we can express $t(x) = e^{-\beta d(x)}$, where $\beta$ is the medium extinction coefficient and d(x) is the scene depth. As multiple solutions exist for a given hazy image, this problem is highly ill-posed.

Fig. 1.

Sample image dehazed results on a real input. The recovered image in (d) has rich details and vivid color information. (Color figure online)

Numerous haze removal methods have been proposed [3–8] in recent years with significant advancements. Most dehazing methods use a variety of visual cues to capture deterministic and statistical properties of hazy images [1, 9–11]. The extracted features model chromatic [1], textural and contrast [10] properties of hazy images to determine the transmission in the scenes. Although these feature representations are useful, the assumptions in these aforementioned methods do not hold in all cases. For example, He et al. [1] assume that the values of dark channel in clear images are close to zero. This assumption is not true when the scene objects are similar to the atmospheric light. As the main goal of image dehazing is to estimate the transmission map from an input image, we propose a multi-scale convolutional neural network (CNN) to learn effective feature representations for this task. Recently, CNNs have shown an explosive popularity [12–15]. The features learned by the proposed algorithm do not depend on statistical priors of the scene images or haze-relevant properties. Since the learned features are based on a data-driven approach, they are able to describe the intrinsic properties of haze formation and help estimate transmission maps. To learn these features, we directly regress on the transmission maps using a neural network with two modules: the coarse-scale network first estimates the holistic structure of the scene transmission, and then a fine-scale network refines it using local information and the output from the coarse-scale module. This removes spurious pixel transmission estimates and encourages neighboring pixels to have the same labels. Based on this premise, we evaluate the proposed algorithm against the state-of-the-art methods on numerous datasets comprised of synthetic and real-world hazy images.

The contributions of this work are summarized as follows. First, we propose a multi-scale CNN to learn effective features from hazy images for the estimation of scene transmission map. The scene transmission map is first estimated by a coarse-scale network and then refined by a fine-scale network. Second, to learn the network, we develop a benchmark dataset consisting of hazy images and their transmission maps by synthesizing clean images and ground truth depth maps from the NYU Depth database [16]. Although the network is trained with the synthetic dataset, we show the learned multi-scale CNN is able to dehaze real-world hazy images well. Third, we analyze the differences between traditional hand-crafted features and the features learned by the proposed multi-scale CNN model. Finally, we show that the proposed algorithm is significantly faster than existing image dehazing methods.

2 Related Work

As image dehazing is ill-posed, early approaches often require multiple images to deal with this problem [17–22]. These methods assume that there are multiple images from the same scene. However, in most cases there only exists one image for a specified scene. Another line of research work is based on physical properties of hazy images. For example, Fattal [23] proposes a refined image formation model for surface shading and scene transmission. Based on this model, a hazy image can be separated into regions of constant albedo, and then the scene transmission can be inferred. Based on a similar model, Tan [10] proposes to enhance the visibility of hazy images by maximizing their local contrast, but the restored images often contain distorted colors and significant halos.

Numerous dehazing methods based on the dark channel prior [1] have been developed [24–27]. The dark channel prior has been shown to be effective for image dehazing. However, it is computationally expensive [28–30] and less effective for the scenes where the color of objects are inherently similar to the atmospheric light. A variety of multi-scale haze-relevant features are analyzed by Tang et al. [2] in a regression framework based on random forests. Nevertheless, this feature fusion approach relies largely on the dark channel features. Despite significant advances in this field, the state-of-the-art dehazing methods [2, 11, 29] are developed based on hand-crafted features.

3 Multi-scale CNN for Transmission Maps

Given a single hazy input, we aim to recover the latent clean image by estimating the scene transmission map. The main steps of the proposed algorithm are shown in Fig. 2(a). We first describe how to estimate the scene transmission map t(x).

Fig. 2.

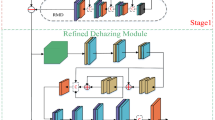
(a) Main steps of the proposed single-image dehazing algorithm. For training the multi-scale network, we synthesize hazy images and the corresponding transmission maps based on depth image dataset. In the test stage, we estimate the transmission map of the input hazy image based on the trained model, and then generate the dehazed image using the estimated atmospheric light and computed transmission map. (b) Proposed multi-scale convolutional neural network. Given a hazy image, the coarse-scale network (the green dashed rectangle) predicts a holistic transmission map and feeds it to the fine-scale network (the orange dashed rectangle) in order to generate a refined transmission map. (Color figure online)

For each scene, we propose to estimate the scene transmission map t(x) based on a multi-scale CNN. The coarse structure of the scene transmission map for each image is obtained from the coarse-scale network, and then refined by the fine-scale network. Both coarse and fine scale networks are applied to the original input hazy image. In addition, the output of the coarse network is passed to the fine network as additional information. Thus, the fine-scale network can refine the coarse prediction with details. The architecture of the proposed multi-scale CNN for learning haze-relevant features is shown in Fig. 2(b).

3.1 Coarse-Scale Network

The task of the coarse-scale network is to predict a holistic transmission map of the scene. The coarse-scale network (in the top half of Fig. 2(b)) consists of four operations: convolution, max-pooling, up-sampling and linear combination.

Convolution Layers: This network takes an RGB image as input. The convolution layers consist of filter banks which are convolved with the input feature maps. The response of each convolution layer is given by $f_n^{l+1} = \sigma (\sum _{m}(f_m^{l}*k_{m,n}^{l+1})+b_n^{l+1})$, where $f_n^l$ and $f_m^{l+1}$ are the feature maps of the current layer l and the next layer $l+1$, respectively. In addition, k is the convolution kernel, indices (m, n) show the mapping from the current layer $m^{th}$ feature map to the next layer $n^{th}$, and $*$ denotes the convolution operator. The function $\sigma (\cdot )$ denotes the Rectified Linear Unit (ReLU) on the filter responses and b is the bias.

Max-Pooling: We use max-pooling layers with a down-sampling factor of 2 after each convolution layer.

Up-Sampling: In our framework, the size of the ground truth transmission map is the same as the input image. However, the size of feature maps is reduced to half after max-pooling layers. Therefore, we add an up-sampling layer [31] to ensure that the sizes of output transmission maps and input hazy images are equal. Although we can alternatively remove the max-pooling and up-sampling layers to achieve the same goal, this method would reduce the non-linearity of the network [31], which is less effective (See Sect. 6.3). The up-sampling layer follows the pooling layer and restores the size of sub-sampled features while retaining the non-linearity of the network. The response of each up-sampling layer is defined as $f_n^{l+1}(2x-1:2x,2y-1:2y) = f_n^{l}(x,y)$. This function copies a pixel value at location (x, y) from the max-pooled features to a $2\times 2$ block in the following up-sampling layer. Since each block in the up-sampling layer consists of the same value, the back-propagation rule of this layer is simply the average-pooling layer in the reverse direction, with a scale of 2, $f_n^{l}(x,y) = \frac{1}{4}\sum _{2\times 2} f_n^{l+1}(2x-1:2x,2y-1:2y)$.

Linear Combination: In our coarse-scale convolution network, the features in the penultimate layer before the output have multiple channels. Therefore, we need to combine the feature channels from the last up-sampling layer through a linear combination [31]. A sigmoid activation function is then applied to produce the final output and the response is given by $t_c = s(\sum _{n}w_nf_n^p + b)$, where $t_c$ denotes the output scene transmission map in the coarse-scale network, n is the feature map channel index, $s(\cdot )$ is a sigmoid function, and $f_n^p$ denotes the penultimate feature maps before the output transmission map. In addition, w and b are weights and bias of the linear combination, respectively.

3.2 Fine-Scale Network

After considering an entire image to predict the rough scene transmission map, we make refinements using a fine-scale network. The architecture of the fine-scale network stack is similar to the coarse-scale network except the first and second convolution layers. The structure of our fine-scale network is shown in the bottom half of Fig. 2(b) where the coarse output transmission map is used as an additional feature map. By design, the size of the coarse prediction is the same as the output of the first up-sampling layer. We concatenate these two together and use the predicted coarse transmission map combined with the learned feature maps in the fine-scale network to refine the transmission map.

3.3 Training

Learning the mapping between hazy images and corresponding transmission maps is achieved by minimizing the loss between the reconstructed transmission $t_i(x)$ and the corresponding ground truth map $t_i^*(x)$,

$$\begin{aligned} L(t_i(x),t_i^*(x)) = \frac{1}{q}\sum _{i=1}^{q}||t_i(x)-t_i^*(x)||^2, \end{aligned}$$

(2)

where q is the number of hazy images in the training set. We minimize the loss using the stochastic gradient descent method with the backpropagation learning rule [12, 32, 33]. We first train the coarse network, and then use the coarse-scale output transmission maps to train the fine-scale network. The training loss (2) is used in both coarse- and fine-scale networks.

4 Dehazing with the Multi-scale Network

Atmospheric Light Estimation: In addition to scene transmission map t(x), we need to estimate the atmospheric light $\varvec{A}$ in order to recover the clear image. From the hazy image formation model (1), we derive $\varvec{I}(x) = \varvec{A}$ when $t(x)\rightarrow 0$. As the objects that appear in outdoor images can be far from the observers, the range of depth d(x) is $[0, +\infty )$, and we have $t(x)=0$ when $d(x)\rightarrow \infty$. Thus we estimate the atmosphere light $\varvec{A}$ by selecting $0.1\,\%$ darkest pixels in a transmission map t(x). Among these pixels, the one with the highest intensity in the corresponding hazy image $\varvec{I}$ is selected as the atmospheric light.

Haze Removal: After $\varvec{A}$ and t(x) are estimated by the proposed algorithm, we recover the haze-free image using (1). However, the direct attenuation term $\varvec{J}(x)t(x)$ may be close to zero when the transmission t(x) is close to zero [1]. Therefore, the final scene radiance J(x) is recovered by

$$\begin{aligned} \varvec{J}(x)=\dfrac{\varvec{I}(x)-\varvec{A}}{\max \{0.1, t(x) \}} +\varvec{A}. \end{aligned}$$

(3)

5 Experimental Results

We quantitatively evaluate the proposed algorithm on two synthetic datasets and real-world hazy photographs, with comparisons to the state-of-the-art methods in terms of accuracy and run time. The MATLAB code is available at https://sites.google.com/site/renwenqi888/research/dehazing/mscnndehazing.

5.1 Experimental Settings

We use 3 convolution layers for both coarse-scale and fine-scale networks in our experiments. In the coarse-scale network, the first two layers consist of 5 filters of size $11\times 11$ and $9\times 9$, respectively. The last layer consists of 10 filters with size $7\times 7$. In the fine-scale network, the first convolution layer consists of 4 filters of size $7\times 7$. We then concatenate these four feature maps with the output from the coarse-scale network together to generate the five feature maps. The last two layers consist of 5 and 10 filters with size $5\times 5$ and $3\times 3$, respectively.

Both the coarse and fine scale networks are trained by the stochastic gradient descent method with 0.9 momentum. We use a batch size of 100 images ($320\times 240$ pixels), the initial learning rate is 0.001 and decreased by 0.1 after every 20 epochs and the epoch is set to be 70. The weight decay parameter is $5\times 10^{-4}$ and the training time is approximately 8 h on a desktop computer with a 2.8 GHz CPU and an Nvidia K10 GPU.

5.2 Training Data

To train the multi-scale network, we generate a dataset with synthesized hazy images and their corresponding transmission maps. We randomly sample 6, 000 clean images and the corresponding depth maps from the NYU Depth dataset [16] to construct the training set. In addition, we generate a validation set of 50 synthesized hazy images using the Middlebury stereo database [34–36].

Given a clear image $\varvec{J}(x)$ and the ground truth depth d(x), we synthesize a hazy image using the physical model (1). We generate the random atmospheric light $\varvec{A}=[k,k,k]$, where $k\in [0.7,1.0]$, and sample three random $\beta \in [0.5,1.5]$ for every image. We do not use small $\beta \in (0, 0.5)$ because it would lead to thin haze and boost noise [1]. On the other hand, we do not use large $\beta \in (1.5, \infty )$ as the resulting transmission maps are close to zero. Therefore, we have 18, 000 hazy images and transmission maps (6,000 images $\times$ 3 medium extinction coefficients $\beta$) in the training set. All the training images are resized to the canonical size of $320 \times 240$ pixels.

Fig. 3.

Dehazed results on synthetic hazy images using stereo images: Bowling, Aloe, Baby, Monopoly and Books. (Color figure online)

5.3 Quantitative Evaluation on Benchmark Dataset

We compare the proposed algorithm with the state-of-the-art dehazing methods [1, 2, 27, 28] using the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity (SSIM) metrics. We use five examples: Bowling, Aloe, Baby, Monopoly and Books for illustration. Figure 3(a) shows the input hazy images which are synthesized from the haze-free images with known depth maps [34]. As the method by He et al. [1] assumes that the dark channel values of clear images are zeros, it tends to overestimate the haze thickness and results in darker results as shown in Fig. 3(b). We note that the dehazed images generated by Meng et al. [27] and Tarel and Hautiere [28] tend to have some color distortions. For example, the colors of the Books dehazed image become darker as shown in Fig. 3(c) and (d). Although the dehazed results by Tang et al. [2] are better than those by [1, 27, 28], the colors are still darker than the ground truth. In contrast, the dehazed results by the proposed algorithm in Fig. 3(e) are close to the ground truth haze-free images, which indicates that better transmission maps are estimated. Figure 4 shows that the proposed algorithm performs well on each image against the state-of-the-art dehazing methods [1, 2, 27, 28] in terms of PSNR and SSIM.

Fig. 4.

Quantitative comparisons of the dehazed images shown in Fig. 3.

Fig. 5.

Dehazed results on our synthetic images. The red and yellow rectangles are for comparison of our method with [1] and [27] respectively. (Color figure online)

New Synthetic Dataset: For quantitative performance evaluation, we construct a new dataset of synthesized hazy images. We select 40 images and their depth maps from the NYU Depth dataset [16] (different from those that used for training) to synthesize 40 transmission maps and hazy images. Figure 5 shows some dehazed images by different methods. The estimated transmission maps by He et al. [1] are uniform and the values almost do not vary with scene depth, and thus the haze thickness in some slight hazy regions is overestimated. This indicates that the dehazed results tend to be darker than the ground truth images in some regions, e.g., the chairs in the first image and the beds in the second and third images. We note that the dehazed results are similar to those by He et al. [1] in Fig. 3(b). Although the estimated transmission maps by Meng et al. [27] in Fig. 5(d) vary with scene depth, the final dehazed images contain some color distortions, e.g., the floor color is changed from gray to blue in the first image. The regions that contain color distortions in the dehazed images correspond to the darker areas in the estimated transmission maps. Figure 5(e) shows the estimated transmission maps and the final recovered images by the proposed algorithm. Overall, the dehazed results by the proposed algorithm have higher visual quality and less color distortions. The qualitative results are also reflected by the quantitative PSNR and SSIM metrics shown in Table 1.

Table 1. Average PSNR and SSIM of dehazed results on the new synthetic dataset.

Table 2. Average run time (in seconds) on test images.

Fig. 6.

Visual comparison for real image dehazing. (Color figure online)

Fig. 7.

Visual comparison for real image dehazing. (Color figure online)

5.4 Run Time

The proposed algorithm is more efficient than the state-of-the-art image dehazing methods [1, 11, 23, 25, 27] in terms of run time. We use the five images in Fig. 3 and the 40 images in the new synthetic dataset for evaluation. All the methods are implemented in MATLAB, and we evaluate them on the same machine without GPU acceleration (Intel CPU 3.40 GHz and 16 GB memory). The average run time using two image resolutions is shown in Table 2.

5.5 Real Images

Although our multi-scale network is trained on synthetic indoor images, we note that it can be applied for outdoor images as well. We evaluate the proposed algorithm against the state-of-the-art single image dehazing methods [1, 2, 10, 23, 27, 28] using six challenging real images as shown in Figs. 6 and 7. More results can be found in the supplementary material. In Fig. 6, the dehazed Yosemite image by Tan [10] and the dehazed Canyon image by Fattal [23] have significant color distortions and miss most details as shown in (b) and (c). The dehazing method of He et al. [1] tend to overestimate the thickness of the haze and produce dark results. The method by Meng et al. [27] can augment the image details and enhance the image visibility. However, the colors in the recovered images still have color distortions. For example, the rock color is changed from gray to yellow in the Yosemite image in (e). In Fig. 7, the dehazing methods of Tarel et al. [28] and Tang et al. [2] overestimate the thickness of the haze and generate darker images than others. The results by Meng et al. [27] have some remaining haze as shown in the first line in Fig. 7(c). In contrast, the dehazed results by the proposed algorithm are visually more pleasing in dense haze regions without color distortions or artifacts.

Fig. 8.

(a) A multi-scale network with three scales. The output of each scale serves as an additional feature in next scale. (b) Comparisons among the first, second and third scale networks. The network with more scales does not lead to better results. (c) Comparisons of one CNN with more layers and the proposed multi-scale CNN. (Color figure online)

6 Analysis and Discussions

6.1 Generalization Capability

As shown in Sect. 5.5, the proposed multi-scale network generalizes well for outdoor scenes. In the following, we explain why indoor scenes help for outdoor image dehazing.

The key observation is that image content is independent of scene depth and medium transmission [2], i.e., the same image (or patch) content can appear at different depths in different images. Therefore, although the training images have relatively shallow depths, we could increase the haze concentration by adjusting the value of the medium extinction coefficient $\beta$. Based on this premise, the synthetic transmission maps are independent of depth d(x) and cover the range of values in real transmission maps.

6.2 Effectiveness of Fine-Scale Network

In this section we analyze how the fine-scale network helps estimate scene transmission maps. The transmission map from the coarse-scale network serves as additional features in the fine-scale network, which greatly improve the final estimation of scene transmission map. The validation cost convergence curves (the blue and red lines) in Fig. 8(b) show that using a fine-scale network could significantly improve the transmission estimation performance. Furthermore, we also train a network with three scales as shown in Fig. 8(a). The output from the second scale also serves as additional features in the third scale network. In addition, we use the same architecture for the third scale as for the second scale network. However, we find that networks with more scales do not help generate better results as shown in Fig. 8(b). The results also show that the proposed network architecture is compact and robust for image dehazing.

To better understand how the fine-scale network affects our method, we conduct a deeper architecture by adding more layers in the single scale network. Figure 8(c) shows that the CNN with more layers does not perform well compared to the proposed multi-scale CNN. This can be explained by that the output from the coarse-scale network provides sufficiently important features as the input for the fine-scale network. We note that similar observations have been reported in SRCNN [37], which indicates that the effectiveness of deeper structures for low-level tasks is not as apparent as that shown in high-level tasks (e.g., image classification). We also show an example of dehazed results with and without the fine-scale network in Fig. 9. Without the fine-scale network, the estimated transmission map lacks fine details and the edges of rock do not match with the input hazy image, which accordingly lead to the dehazed results containing halo artifacts around the rock edge. In contrast, the transmission map generated with fine-scale network is more informative and thus results in a clearer image.

Fig. 9.

Effectiveness of the proposed fine-scale network.(a) Hazy image. (b) and (d) are the transmission map and dehazed result without the fine-scale network. (g) and (i) denote transmission map and dehazed result with the fine-scale network. (f), (c), (e), (h), and (j) are the zoom-in views in (a), (b), (d), (g), and (i), respectively.

Fig. 10.

Effect of up-sampling layers.(a) Input hazy image. (b) Dehazed result with stride of 1 for all layers. (c) Dehazed result without pooling layers.(d) Our result.

Fig. 11.

Effectiveness of learned features. With these diverse features (f) automatically learned from the proposed algorithm, our dehazed result is sharper and visually more pleasing than others. (Color figure online)

6.3 Effectiveness of Up-Sampling Layers

For image dehazing, the size of the ground truth transmission map is the same as that of the input image. To maintain identical sizes, we can (i) set the strides to 1 in all convolutional and pooling layers, (ii) remove the max-pooling layers, or (iii) add the up-sampling layers to keep the size of input and output the same. However, it requires much more memory and longer training time when the stride is set to 1. On the other hand, the non-linearity of the network is reduced if the max-pooling layers are removed. Thus, we add the up-sampling layers in the proposed network model as show in Fig. 2. Figure 10 shows the dehazed images using these three trained networks. As shown in Fig. 10, the dehazed image from the network with up-sampling layers is visually more pleasing than the others. Although the dehazed result in Fig. 10(b) is close to the one in (d), setting stride to 1 slows down the training process and requires much more memory compared with the proposed network using the up-sampling layers.

6.4 Effects of Different Features

In this section, we analyze the differences between the traditional hand-crafted features and the features learned by the proposed multi-scale CNN model. Traditional methods [1, 2, 10, 38] focus on designing hand-crafted features while our method learns the effective haze-relevant features automatically.

Figure 11(a) shows an input hazy image. The dehazed result only using dark channel feature (b) is shown in (c). In the recent work, Tang et al. [2] propose a learning based dehazing model. However, this work involves a considerable amount of effort in the design of hand-crafted features including dark channel, local max contrast, local max saturation and hue disparity features as show in (d). By fusing all these features in a regression framework based on random forests, the dehazed result is shown in (e). In contrast, our data-driven framework automatically learns the effective features. Figure 11(f) show some features automatically learned by the multi-scale network for the input image. These features are randomly selected from the intermediate layers of the multi-scale CNN model. As shown in Fig. 11(f), the learned features include various kinds of information for the input, including luminance map, intensity map, edge information and amount of haze, and so on. More interestingly, some features learned by the proposed algorithm are similar to the dark channel and local max contrast as shown in the two red rectangles in Fig. 11(f), which indicates that the dark channel and local max contrast priors are useful for dehazing as demonstrated by prior studies. With these diverse features learned from the proposed algorithm, the dehazed image shown in Fig. 11(g) is sharper and visually more pleasing.

6.5 Failure Case

Our multi-scale CNN model is trained on the synthetic dataset which is created based on the hazy model (1). As the hazy model (1) usually does not hold for the nighttime hazy images [39, 40], our method is less effective for such images. One failure example is shown in Fig. 12. In future work we will address this problem by developing an end-to-end network to simultaneously estimate the transmission map and atmospheric light for the input hazy image.

Fig. 12.

Failure case for nighttime hazy image.

7 Conclusions

In this paper, we address the image dehazing problem via a multi-scale deep network which learns effective features to estimate the scene transmission of a single hazy image. Compared to previous methods which require carefully designed features and combination strategies, the proposed feature learning method is easy to implement and reproduce. In the proposed multi-scale model, we first use a coarse-scale network to learn a holistic estimation of the scene transmission, and then use a fine-scale network to refine it using local information and the output from the coarse-scale network. Experimental results on synthetic and real images demonstrate the effectiveness of the proposed algorithm. In addition, we show that our multi-scale network generalizes and performs well for real scenes.