Multi-Task Zero-Shot Action Recognition with Prioritised Data Augmentation

Abstract

Zero-Shot Learning (ZSL) promises to scale visual recognition by bypassing the conventional model training requirement of annotated examples for every category. This is achieved by establishing a mapping connecting low-level features and a semantic description of the label space, referred as visual-semantic mapping, on auxiliary data. Re-using the learned mapping to project target videos into an embedding space thus allows novel-classes to be recognised by nearest neighbour inference. However, existing ZSL methods suffer from auxiliary-target domain shift intrinsically induced by assuming the same mapping for the disjoint auxiliary and target classes. This compromises the generalisation accuracy of ZSL recognition on the target data. In this work, we improve the ability of ZSL to generalise across this domain shift in both model- and data-centric ways by formulating a visual-semantic mapping with better generalisation properties and a dynamic data re-weighting method to prioritise auxiliary data that are relevant to the target classes. Specifically: (1) We introduce a multi-task visual-semantic mapping to improve generalisation by constraining the semantic mapping parameters to lie on a low-dimensional manifold, (2) We explore prioritised data augmentation by expanding the pool of auxiliary data with additional instances weighted by relevance to the target domain. The proposed new model is applied to the challenging zero-shot action recognition problem to demonstrate its advantages over existing ZSL models.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Action recognition has long been a central topic in computer vision [1]. A major thrust in action recognition is scaling methods to a wider and finer range of categories [2–4]. The traditional approach to dealing with a growing number of categories is to collect labeled training examples of each new category. This is not scalable, particularly in the case of actions, due to the temporally extended nature of videos compared to images, making annotation (segmentation in both space and time) more onerous than for images. In contrast, the Zero-Shot Learning (ZSL) [5, 6] paradigm is gaining significant interest by providing an alternative to classic supervised learning which does not require an ever increasing amount of annotation. Instead of collecting training data for the target categories¹ to be recognised, a classifier is constructed by re-using a visual to semantic space mapping pre-learned on a training/auxiliary set² of totally independent (disjoint) categories. Specifically training class labels are represented in a vector space such as attribute [5, 7] or word-vectors [6, 8]. Such vector representations of class-labels are referred to as semantic label embeddings [7]. A mapping (e.g. regression [9] or bilinear model [7]) is learned between low-level visual features and their semantic embeddings. This mapping is assumed to generalise and be re-used to project visual features of target classes into semantic embedding space and matched against target class embeddings.

A fundamental challenge for ZSL is that in the context of supervised learning of the visual-semantic mapping, the ZSL setting violates the traditional assumption of supervised learning [10] – that training and testing data are drawn from the same distribution. Thus its efficacy is reduced by domain shift [11–13]. For example, when a regressor is used to map visual features to semantic embedding, the disjoint training and testing classes in ZSL intrinsically require the regressor to generalise out-of-bounds. This inherently limits the accuracy of ZSL recognition. In this work, we address the issue of the generalisation capability of a ZSL mapping regressor from both the model- and data-centric perspectives: (1) by proposing a more robust regression model with better generalisation properties, and (2) improving model learning by augmenting auxiliary data with a re-weighted additional dataset according to the relevance to the target problem.

Multi-Task Embedding. When establishing the mapping between visual features and semantic embeddings, most ZSL methods learn each dimension of this mapping independently – whether semantic embedding is discrete as in the case of attributes [5, 7], or continuous as in the case of word vectors [6, 8]. This strategy is likely to overfit to the training classes because it treats each dimension of the label in semantic embedding independently despite the labels living on a non-uniform manifold [14] and many independent mappings result in a large number of parameters to be learned. We denote this conventional approach as Single-Task Learning (STL) due to the independent learning of mappings for each attribute/word dimension. In contrast, we advocate a Multi-Task Learning (MTL) [10, 15, 16] regression approach to mapping visual features and their semantic embeddings. By constraining the mapping parameters of each learning task to lie closely on a low-dimensional manifold, we gain two advantages: (1) Exploiting the relation between the response variables (dimensions of the label embedding), (2) reducing the total number of parameters to fit. The resulting visual-semantic mapping is more robust to the domain shift between ZSL training and testing classes. As a helpful byproduct, the MTL mapping, provides a lower dimensional latent space in which the nearest neighbour (NN) matching required by ZSL can be better performed [17] compared to the usual higher dimensional label semantic embedding space.

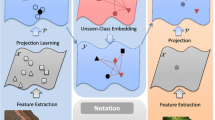
Prioritised Auxiliary Data Augmentation for Domain Adaptation. From a data-, rather than model-centric perspective, studies have also attempted to improve the generalisation of ZSL methods by augmenting³ the auxiliary dataset with additional datasets containing a wider array of classes and instances [9, 18]. The idea is that including a broader additional set should provide better coverage of the visual feature and label embedding spaces, therefore helping to learn a visual-semantic mapping that better generalises to target classes, and thus improves performance when representing and recognising target classes. However, existing studies on exploring this idea have been rather crude, e.g. simply expanding the training dataset by blindly concatenating auxiliary set with additional data [9]. This is not only inefficient but also dangerous, because it does not take into account the (dis)similarity between the extra incorporated data and the target classes for recognition, thus risking negative transfer [10]. In this work, we address the issue that auxiliary and target data/categories will have different marginal distributions (Fig. 1). We selectively re-weight those relevant instances/classes from the auxiliary data that are expected to improve the visual-semantic mapping in the context of the specific target classes to be recognised (target domain). We formulate this prioritised data augmentation as a domain adaptation problem by minimizing the discrepancy between the marginal distributions of the auxiliary and target domains. To achieve this, we propose an importance weighting strategy to re-weight each auxiliary instance in order to minimise the discrepancy. Specifically we generalise the classic Kullback-Leibler Importance Estimation Procedure (KLIEP) [19, 20] to the zero-shot learning problem.

Fig. 1.

Two strategies to improve generalisation of visual-semantic mapping in ZSL. Left: Importance weighting to prioritise auxiliary data relevant to the target domain. Right: Learning the mapping from visual features $\mathbf {X}$ to semantic embedding $\mathbf {Z}$ by MTL reduces overfitting, and also provides a latent lower dimensional representation $\{\mathbf {l}_t\}$ to benefit nearest neighbour matching.

2 Related Work

Zero-Shot Learning. Zero-shot Learning (ZSL) [5] aims to generalize existing knowledge to recognize new categories without training examples by re-using a mapping learned from visual features to their semantic embeddings. Commonly used label embeddings are semantic attributes [5, 11, 21] and word-vectors [6, 9]. The latter has the advantage of being learned from data without requiring manual annotation. Commonly used visual-semantic mappings include linear [12] and non-linear regression [6, 9, 11], classification [5, 21], and bilinear ranking [7].

Existing ZSL methods suffer from weak generalisation due to the domain-shift induced by disjoint auxiliary-target classes, an issue that has recently been highlighted explicitly in the literature [8, 11–13]. Attempts to address this so far include post-processing heuristics [11–13], sparse coding regularisation [8], and simple blind enlarging of the training set with auxiliary data [9]. In contrast to [8, 9], we focus on: (1) Building a visual-semantic mapping with intrinsically better generalisation properties, and (2) re-weighting the auxiliary set to prioritise auxiliary instances most relevant to the target instances and classes. Our method is complementary to [11, 12] and can benefit from these heuristics.

Zero-Shot Action Recognition. Among many ZSL tasks in computer vision, zero-shot action recognition [9, 21–24] is of particular interest because of the lesser availability of labelled video compared to image data and videos are more difficult to label than static images due to extended temporal duration and more complex ontology. ZSL action recognition is much less studied than still image recognition, and existing video-ZSL methods suffer from the same domain-shift drawbacks highlighted above.

Multi-Task Regression Learning. Multi-Task Learning (MTL) [10, 25] aims to improve generalisation in a set of supervised learning tasks by modelling and exploiting shared knowledge across the tasks. An early study [15] proposed to model the weight vector for each task $t$ as a sum of a shared global task $\mathbf {w}_0$ and task specific parameter vector $\mathbf {w}_t$. However, the assumption of a globally shared underlying task is too strong, and risks inducing negative transfer [10]. This motivates the Grouping and Overlapping Multi-Task Learning (GOMTL) [16] framework which instead assumes that each task’s weight vector is a task-specific combination of a small set of latent basis tasks. This constrains the parameters of all tasks to lie on a low dimensional manifold.

MTL methods have been studied for action recognition [26–29]. However, all of these studies focus on improving standard supervised action recognition with multi-task sharing. For example, considering each of multiple views [28, 29], feature modalities [27], or – most obviously – action categories [26] as different tasks. Multi-view/multi-feature recognition is orthogonal to our work, while the later ones are concerned with supervised recognition, and cannot be generalised to the ZSL scenario. In contrast, we take a very different approach and treat each dimension of the visual-semantic mapping as a task, in order to leverage MTL to improve auxiliary-target generalisation across the disjoint target categories. Finally, we note that the use of MTL to learn the visual semantic mapping provides a further benefit of a lower-dimensional space in which zero-shot recognition can be better performed due to being more meaningful for NN matching [17].

Importance Weighting for Domain Adaptation. Domain shift is a widely studied problem in transfer learning [10], although it is usually induced by sampling bias [30, 31] or sensor change [32] rather than the disjoint categories in ZSL. Importance weighting (IW) [19, 31] has been one of the main adaptation techniques to address this issue. The prior work in this area is designed for the standard domain transfer problem in a supervised learning setting [33], while we are the first to generalise it to the zero-shot learning scenario. The IW technique we generalise is related to another domain adaptation approach based on discovering a feature mapping to minimise the Maximum Mean Discrepancy (MMD) [34, 35] between distributions. However MMD, is less appropriate for us due to focus on feature mapping rather than instance reweighing, and our expectation is that only subsets of auxiliary instances will be relevant to the target rather than the holistic auxiliary set.

Contributions. This paper contributes both model- and data-centric strategies to improve ZSL action recognition: (1) We formulate learning a more generalisable visual-semantic mapping in ZSL as a Multi-Task Learning problem with a lower-dimensional latent semantic embedding space for more effective matching. (2) We improve visual-semantic regression generalisation by prioritised data augmentation using importance weighting of auxiliary instances relevant to the target domain.

Table 1. Notation summary

3 Visual-Semantic Mapping with Multi-Task Regression

In ZSL, we aim to recognise action categories $\mathbf {Y}$ given visual features $\mathbf {X}$ where training/auxiliary and testing/target categories do not overlap $\mathcal {Y}^{tr}\cap \mathcal {Y}^{te}=\emptyset$. The key method by which ZSL is achieved is to embed each category label in $\mathcal {Y}$ into a semantic label embedding space $\mathcal {Z}$ which provide a vector representation of any nameable category. Table 1 summarises the notation used in the subsequent sections.

3.1 Training a Visual Semantic Mapping

We first introduce briefly the conventional single task learning using regression for visual-semantic mapping [9, 11, 12].

Single-Task Regression. Given a matrix $\mathbf {V}$ describing the embedded action names⁴, and per-video binary labels $\mathbf {Y}$, we firstly obtain the label embedding of any action label for a video clip as $\mathbf {z}_i=\mathbf {V}\mathbf {y}_i$. We then learn a visual-semantic mapping function $f:\mathcal {X}\rightarrow \mathcal {Z}$ on the training categories. Given a loss function $l(\cdot ,\cdot )$, we learn the mapping f by optimising Eq. (1) where $\varOmega (f)$ denotes regularization on the mapping:

$$\begin{aligned} {\begin{matrix} \min \limits _{f}\frac{1}{n^{tr}_x}\sum \limits _{i=1}^{n^{tr}_x} l\left( f(\mathbf {x}_i),\mathbf {z}_{i}\right) +\varOmega (f).\\ \end{matrix}} \end{aligned}$$

(1)

The most straightforward choice of mapping f and loss l is linear $f(\mathbf {x})=\mathbf {W}\mathbf {x}$, and square error respectively, which results in a regularized linear (ridge) regression problem: $l\left( f(\mathbf {x}_i),\mathbf {z}_{i}\right) =||\mathbf {z}_i-\mathbf {W}\mathbf {x}_i||_2^2$. A closed-form solution to $\mathbf {W}$ can then be obtained by $\mathbf {W} = \mathbf {Z}\mathbf {X}^T\left( \mathbf {XX}^T+\lambda n_x^{tr}\mathbf {I}\right) ^{-1}$. Each row $\mathbf {w}_d$ of regressor $\mathbf {W}$ maps visual feature $\mathbf {x}_i$ to dth dimension of response variable $\mathbf {z}_i$. Since regressors $\{\mathbf {w}_d\}_{d=1\cdots d_z}$ are learned independently from each other this is referred as single-task learning (STL) with each $\mathbf {w}_d$ defining one distinct ‘task’.

From Single to Multi-Task Regression. In the conventional ridge-regression solution to Eq. (1), each task $\mathbf {w}_d$ is effectively learned separately, ignoring any relationship between tasks. We wish to model this relationship by discovering a latent basis of predictors such that tasks $\mathbf {w}_d$ are constructed as linear combinations of T latent tasks $\{\mathbf {a}_t\}_{t=1\cdots T}$. So the dth regression predictor is now modelled as $\mathbf {w}_d=\sum _t{s}_{dt}\mathbf {a}_t=\mathbf {s}_d^T\mathbf {A}$, where $\mathbf {s}_d$ is the combination coefficient for d-th task. Denoting multi-task regression prediction as $f(\mathbf {x}_i,\mathbf {S},\mathbf {A})$, we now optimise:

$$\begin{aligned} \min \limits _{\mathbf {S},\mathbf {A}} \frac{1}{n^{tr}_x}\sum \limits _{i=1}^{n^{tr}_x}l(f(\mathbf {x}_i,\mathbf {S},\mathbf {A}),\mathbf {z}_i) + \lambda \varOmega (S) + \gamma \varPsi (\mathbf {A}). \end{aligned}$$

(2)

Grouping and Overlap Multi-Task Learning. An effective method following the MTL design pattern above is GOMTL [16]. GOMTL uses a $\mathbf {W}=\mathbf {SA}$ task parameter matrix factorisation, where the number of latent tasks T (typically $T< d_z$) is a free parameter. Requiring the combination coefficients $\mathbf {s}_t$ to be sparse, via a $\ell _1$ regulariser, the loss is written as

$$\begin{aligned} \min \limits _{\{\mathbf {s}_t\},\mathbf {A}} \sum \limits _{t=1}^T\frac{1}{n^{tr}_x}\sum \limits _{i=1}^{n^{tr}_x}||\mathbf {z}_{t,i}-\mathbf {s}_t\mathbf {A}\mathbf {x}_i||+\lambda \mathop {\sum }\nolimits _{t=1}^T||\mathbf {s}_t||_1 + \gamma ||\mathbf {A}||_F^2 \end{aligned}$$

(3)

This can be solved by iteratively updating $\mathbf {A}$ and $\mathbf {S}$. When $\mathbf {A}$ is fixed, loss function reduces to a standard L1 regularized (LASSO) regression problem that can be efficiently solved by Alternating Direction Method of Multipliers (ADMM) [36]. When $\mathbf {S}$ is fixed, we can efficiently solve $\mathbf {A}$ by gradient descent.

Regularized Multi-Task Learning (RMTL). The classic RMTL method [15] models task parameters as the sum of a globally shared and task specific parameter vector: $\mathbf w _t=\mathbf a _0+\mathbf a _t$. It can be seen that this corresponds to a special case of GOMTL’s $\mathbf {W}=\mathbf {SA}$ predictor matrix factorisation [25]. Here there are $T=d_z+1$ latent tasks, a fixed task combination vector $\mathbf {s}_t = [1 \quad \mathbf {1}(t=1) \quad \mathbf {1}(t=2) \cdots \mathbf {1}(t=d_z)]^T$ where $\mathbf {1}(\cdot )$ is the indicator function and ${A}=\left[ \mathbf {a}_0^T \mathbf {a}_1^T \cdots \mathbf {a}_{d_{z}}^T\right] ^T$.

Explicit Multi-Task Embedding (MTE). In GOMTL Eq. (3), it can be seen that the label embedding $\mathbf {z}_i$ is approximated from the data by the mapping $\mathbf {s}_t\mathbf {A}\mathbf {x}_i$, and this approximation is reached by combination via the latent representation $\mathbf {A}\mathbf {x}_i$. While GOMTL defines this space implicitly via the learned $\mathbf {A}$, we propose to model it explicitly as $\mathbf {l}_i\approx \mathbf {A}\mathbf {x}_i$. This is so the actual projections $\mathbf {l}_i$ in this latent space can be regularised explicitly, in order to learn a latent space which generalises better to test data, and hence improves ZSL matching later.

Specifically, we split the GOMTL loss $||\mathbf {z}_i-\mathbf {SA}\mathbf {x}_i||^2_2$ into two parts: $||\mathbf {l}_i-\mathbf {A}\mathbf {x}_i||^2_2$ and $||\mathbf {z}_i-\mathbf {S}\mathbf {l}_i||^2_2$ to learn the mapping to the latent space, and from the latent space to the label embedding respectively. This allows us to place additional regularization on $\mathbf {l}_i$ to avoid extreme values in the latent space and thus later improve neighbour matching (Sect. 3.2). Given the large and high dimensional video datasets, we apply Frobenius norm on $\mathbf {S}$ in contrast to GOMTL’s $\ell _1$.

$$\begin{aligned} \min \limits _{\{\mathbf {s}_t\},\mathbf {A},\{\mathbf {l}_i\}}&\quad \sum \limits _{t=1}^T\frac{1}{n^{tr}_x}\sum \limits _{i=1}^{n^{tr}_x}\left( ||\mathbf {z}_{t,i}-\mathbf {s}_t\mathbf {l}_i||^2_2+||\mathbf {l}_i-\mathbf {A}\mathbf {x}_i||^2_2\right) + \nonumber \\&\lambda _S\sum \limits _{t=1}^T||\mathbf {s}_t||_2^2 + \lambda _A||\mathbf {A}||_F^2 +\lambda _L\sum \limits _{i=1}^{n_x^{tr}}||\mathbf {l}_i||_2^2 \end{aligned}$$

(4)

Our explicit multi-task embedding has similarities to [18], but our purpose is multi-task regression for ZSL, rather than embedding for video descriptions. To solve our explicit embedding model we iteratively solve $\mathbf {L}$,$\mathbf {A}$ and $\mathbf {S}$ while fixing the other two. With the $\ell _2$ norm on $\mathbf {S}$, this has a convenient closed-form solution to each parameter:

$$\begin{aligned}&\mathbf {L}=(\mathbf {S}^T\mathbf {S}+(\lambda _L n^{tr}_x + 1)\mathbf {I})^{-1}(\mathbf {S}^T\mathbf {Z}+\mathbf {AX}) \nonumber \\&\mathbf {S}=\mathbf {ZL}^T(\mathbf {LL}^T+\lambda _S n^{tr}_x \mathbf {I})^{-1}\\&\mathbf {A}=\mathbf {LX}^T(\mathbf {XX}^T+\lambda _A n^{tr}_x \mathbf {I})^{-1} \nonumber \end{aligned}$$

(5)

3.2 Zero-Shot Action Recognition

We consider two alternative NN matching methods for zero-shot action prediction that use the MTL mappings described above.

Distributed Space Matching. Given a trained visual-semantic regression f, we project testing set visual feature $\mathbf {x}^{te}$ into the semantic label embedding space. The standard strategy [9, 11, 12] is then to employ NN matching in this space for zero-shot recognition. Specifically, given the matrix of label embeddings for each target category name $\mathbf {V}^{te}$, and using cosine distance norm, the testing video $\mathbf {x}^{te}$ are classified by:

$$\begin{aligned} \mathbf {y}^*=arg\min \limits _{\mathbf {y}^*} ||\mathbf {V}^{te}\mathbf {y}^*-f(\mathbf {x}^{te})|| \end{aligned}$$

(6)

where $f(\mathbf {x}^{te})=\mathbf {Wx}^{te}$ for STL and $f(\mathbf {x}^{te})=\mathbf {SAx}^{te}$ for MTL.

Latent Space Matching. MTL methods provide an alternative to matching in label space: Matching in the latent space. The representation of testing data in this space is the output of latent regressors $\mathbf {l}_{te}=\mathbf {A}\mathbf {x}^{te}$ (Eq. (4)). To get the representation of testing categories in the latent space we invert the combination matrix $\mathbf {S}$ to project target category names $\mathbf {V}^{te}$ into latent space. Specifically we classify by Eq. (7), where $(\mathbf {S}^T\mathbf {S})^{-1}\mathbf {S}^T$ is the Moore-Penrose pseudoinverse.

$$\begin{aligned} \mathbf {y}^*=arg\min \limits _{\mathbf {y}^*} ||(\mathbf {S}^T\mathbf {S})^{-1}\mathbf {S}^T\mathbf {V}^{te}\mathbf {y}^*-\mathbf {Ax}^{te}|| \end{aligned}$$

(7)

NN matching in the latent space is better than in semantic label space because: (i) the dimension is lower $T<d_z$, and (ii) we have explicitly regularised the latent space to be well behaved (Eq. (4)).

4 Importance Weighting

Augmenting auxiliary data with additional examples from other datasets has been proved to benefit learning the visual-semantic mapping [9]. However, simply aggregating auxiliary and additional datasets is not ideal as including irrelevant data risks ‘negative transfer’. Therefore we are motivated to develop methodology to prioritise augmented auxiliary data that is useful for a particular ZSL recognition scenario. Specifically, we learn a per-instance weighting $\omega (\mathbf {x})$ on the auxiliary dataset $\mathbf {X}^{tr}$ to adjust each instance’s contribution according to relevance to the target domain. Because Importance Weighting (IW) adapts auxiliary data to the target domain, we assume a transductive setting with access to testing data $\mathbf {X}^{te}$.

Kullback-Leibler Importance Estimation Procedure (KLIEP). We first introduce the way to estimate a per-instance auxiliary-data weight given the distribution of target data $\mathbf {X}^{te}$. This is based on the idea [19] of minimizing the KL-divergence ($D_{KL}$) between training $p^{tr}(\mathbf {x})$ and testing data distribution $p^{te}(\mathbf {x})$ via learning a weighting function $\omega (\mathbf {x})$. This is formalised in Eq. (8):

$$\begin{aligned} \begin{aligned}&\min \limits _{\omega } D_{KL}(p^{te}(\mathbf {x})| \omega (\mathbf {x})p^{tr}(\mathbf {x}))=\int p^{te}(\mathbf {x})\log \frac{p^{te}(\mathbf {x})}{\omega (\mathbf {x})p^{tr}(\mathbf {x})}d\mathbf {x} \\&\min \limits _{\omega }\int p^{te}(\mathbf {x})\log \frac{p^{te}(\mathbf {x})}{p^{tr}(\mathbf {x})} d\mathbf {x} - \int p^{te}(\mathbf {x})\log \omega (\mathbf {x}) d\mathbf {x} \end{aligned} \end{aligned}$$

(8)

The first term is fixed w.r.t. $\omega (\mathbf {x})$ so the objective to optimise is:

$$\begin{aligned} {\begin{matrix}&\min \limits _{\omega }- \int p^{te}(\mathbf {x})\log \omega (\mathbf {x}) d\mathbf {x} \approx -\frac{1}{n_x^{te}}\sum \limits _{i=1}^{n_x^{te}}\log \omega (\mathbf {x}_i) \end{matrix}} \end{aligned}$$

(9)

Aligning Both Visual Features and Labels. KLIEP is conventionally used for domain adaptation by reweighting instances [19, 33]. In the case of transductive ZSL, we have the target data $\mathbf {X}^{te}$ and category labels $\mathbf {Z}^{te}$ respectively, although not instance-label association which is to be predicted. In this case we can further improve ZSL by extending KLIEP to align training and testing sets in both visual feature and category sense⁵. Specifically, we minimise the kullback-leibler divergence between the target and auxiliary in terms of both the visual and category distributions:

$$\begin{aligned}&\min \limits _{\omega _x,\omega _z}D_{KL}(p^{te}(X)|| \omega _x(\mathbf {X})p^{tr}(\mathbf {X}))+D_{KL}(p^{te}(\mathbf {Z})||\omega _z(\mathbf {Z})p^{tr}(\mathbf {Z})) \nonumber \\&\min \limits _{\omega _x,\omega _z} -\frac{1}{n_x^{te}}\sum \log \omega _x(\mathbf {x}_i^{te}) -\frac{1}{n_x^{te}}\sum \log \omega _z(\mathbf {z}_i^{te}) \end{aligned}$$

(10)

Given both $\mathbf {X}^{te}$ and $\mathbf {Z}^{te}$, we construct the weighting functions as a combination of Gaussian kernels centered at the testing data and categories. Specifically we define $\omega (\mathbf {x},\mathbf {z})=\omega _x(\mathbf {x})+\omega _z(\mathbf {z})$ where $\omega _x(\mathbf {x})$ and $\omega _z(\mathbf {z})$ are calculated as in Eq. (11). Here $\omega (\mathbf {x},\mathbf {z})$ extends the previous notation $\omega (\mathbf {x})$ to indicate giving a weight to each training instance given visual feature $\mathbf {x}$ and class name embedding $\mathbf {z}$. So if there are $n^{tr}_x$ instances, $\omega (\mathbf {x},\mathbf {z})$ returns a weight vector of length $n^{tr}_x$.

$$\begin{aligned} {\begin{matrix} \omega _x(\mathbf {x})=\sum \limits _{i=1}^{n^{te}_x}\alpha _i \phi (\mathbf {x},\mathbf {x}_i^{te}), \quad \omega _z(\mathbf {z})=\sum \limits _{i=1}^{n^{te}_x}\beta _j \phi (\mathbf {z},\mathbf {z}_i^{te}), \quad \phi (\mathbf {x},\mathbf {x}^{te}_i)=exp\left( -\frac{||\mathbf {x}-\mathbf {x}^{te}_i||^2}{2\sigma ^2}\right) \end{matrix}} \end{aligned}$$

(11)

For ease of formulation, we denote $\mathbf {a}=[\alpha _1 \cdots \alpha _{n^{te}_x}]^T$, $\mathbf {b}=[\beta _1 \cdots \beta _{n^{te}_x}]^T$, $\varPhi _{\mathbf {a}}(\mathbf {x})=[\phi (\mathbf {x},\mathbf {x}_1^{te}) \cdots \phi (\mathbf {x},\mathbf {x}_{n^{te}_x}^{te})]^T$ and $\varPhi _{\mathbf {b}}(\mathbf {z})=[\phi (\mathbf {z},\mathbf {z}_1^{te}) \cdots \phi (\mathbf {z},\mathbf {z}_{n^{te}_x}^{te})]^T$. The optimization can be thus written as

$$\begin{aligned} {\begin{matrix}&\min \limits _{\mathbf {a},\mathbf {b}} -\frac{1}{n_x^{te}}\sum \limits _{i=1}^{n_x^{te}}\log \,\mathbf {a}^T\varPhi _\mathbf {a}(\mathbf {x}_i^{te}) -\frac{1}{n_x^{te}}\sum \limits _{i=1}^{n_x^{te}}\log \,\mathbf {b}^T\varPhi _\mathbf {b}(\mathbf {z}_i^{te}), \quad s.t. \quad \frac{1}{n_x^{tr}}\sum \limits _{i=1}^{n_x^{tr}}\omega (\mathbf {x}_i^{tr},\mathbf {z}_i^{tr}) = 1 \end{matrix}} \end{aligned}$$

(12)

The above constrained optimization problem is convex w.r.t. both $\mathbf {a}$ and $\mathbf {b}$. It can be solved by interior point methods using the derivatives in Eq. (13):

$$\begin{aligned} {\begin{matrix}&\nabla \mathbf {a}=-\frac{1}{n_x^{te}}\sum \limits _{i=1}^{n_x^{te}}\frac{1}{\mathbf {a}^T\varPhi _\mathbf {a}(\mathbf {x}_i^{te})}\varPhi _\mathbf {a}(\mathbf {x}_i^{te}), \quad \nabla \mathbf {b}=-\frac{1}{n_x^{te}}\sum \limits _{i=1}^{n_x^{te}}\frac{1}{\mathbf {b}^T\varPhi _\mathbf {b}(\mathbf {z}_i^{te})}\varPhi _\mathbf {b}(\mathbf {z}_i^{te}) \end{matrix}} \end{aligned}$$

(13)

Weighted Visual-Semantic Regression. Given per-instance weights $\omega$ estimated above, we can rewrite the loss function for both single-task ridge regression and multi-task regression in Sect. 3.1 as $\omega _il(f(\mathbf {x}_i,\mathbf {A}),\mathbf {z}_i)$ and $\omega _il(f(\mathbf {x}_i,\mathbf {S},\mathbf {A}),\mathbf {z}_i)$ respectively. All our loss functions have quadratic form, so the weight can be expressed inside the quadratic loss e.g. $\omega _i||\mathbf {z}_i-\mathbf {W}\mathbf {x}_i||^2_2=||\mathbf {z}_i\sqrt{\omega _i}-\mathbf {W}\mathbf {x}_i\sqrt{\omega _i}||_2^2$. Thus to incorporate the weight information we simply replace the original semantic embedding matrix with $\tilde{\mathbf {z}}_i=\mathbf {z}_i\sqrt{\omega _i}$ and data matrix with $\tilde{\mathbf {x}}_i=\mathbf {x}_i\sqrt{\omega _i}$.

5 Experiments

Datasets and Settings. We evaluated our contributions on three human action recognition datasets, HMDB51 [3], UCF101 [4] and Olympic Sports [37]. They contain 6766, 13320, 783 videos and 51, 101, 16 categories respectively. For all datasets we extract improved trajectory feature (ITF) [38], a state-of-the-art space-time feature representation for action recognition. We use Fisher Vectors (FV) [39] to encode three raw descriptors (HOG, HOF and MBH). Each descriptor is reduced to half of its original dimension by PCA, resulting in a 198 dim representation. Then we randomly sample 256,000 descriptors from all videos and learn a Gaussian Mixture with 128 components to obtain the FVs. The final dimension of FV encoded feature is $2\times 128\times 198=50688$ dimensions. For the label-embedding, we use 300-dimensional word2vec [40]. We use $T=n^{tr}_c$ latent tasks, and cross-validation to determine regularisation strength hyper-parameters for the models⁶.

5.1 Visual-Semantic Mappings for Zero-Shot Action Recognition

Evaluation Criteria. To evaluate zero-shot action recognition, we divide each dataset evenly into training and testing parts with 5 random splits. Using classification accuracy for HMDB51 and UCF101 and average precision for Olympic Sports as the evaluation metric, the average and standard deviation over the 5 splits are reported for each dataset.

Compared Methods. We study the efficacy of our contributions by evaluating the different visual-semantic mappings presented in Sect. 3.1. We compare MTL-regression methods with conventional STL Ridge Regression (denoted RR) for ZSL. For RR/STL, nearest neighbour matching is used to recognise target categories. Note that the RR+NN method here corresponds to the core strategy used by [9, 11, 12]. The multi-task models we explore include: RMTL [15]: assumes each task’s predictor is the sum of a global latent vector and a task-specific vector. GOMTL [16]: Uses a predictor-matrix factorisation assumption in which tasks’ predictors lie on a low-dimensional subspace. Multi-Task Embedding (MTE):    Our model differs from GOMTL in that it explicitly models and regularises a lower dimensional latent space. For the multi-task methods, we also compare the ZSL matching strategies introduced in Sect. 3.2: Distributed: Standard NN matching (Eq. (6)), and Latent: our proposed latent-space matching (Eq. (7)).

Table 2. Visual-semantic mappings for zero-shot action recognition: MTL ($\checkmark$) versus STL (X). Latent matching ($\checkmark$) versus distributed (X) matching

Results: The comparison of single task ridge regression with our multi-task methods is presented in Table 2. From these results we make the following observations: (i) Overall our multi-task methods improve on the corresponding single-task baseline of RR. MTL regression (RMTL, GOMTL and MTE) improves single-task ridge regression by 5–10% in relative terms, with the biggest margins visible on the Olympic Sports dataset. (ii) Within multi-task models, the GOMTL with sparse $\ell _1$ regularization outperforms RMTL. This suggests learning the task combination $\mathbf {S}$ from data is better than fixing it as in RMTL. (iii) Our MTE generally outperforms other multi-task methods supporting the explicit modelling and regularisation of the latent space. (iv) In most cases, NN matching in the latent space improve zero-shot performance. This is likely due to the lower dimension of the latent space compared to the dimension of the original word vector embedding, making NN matching more meaningful [17].

5.2 Importance Weighted Data Augmentation

We next evaluate the impact of importance weighting in data augmentation for zero-shot action recognition. We perform the same 5 random split benchmark for each dataset. For data augmentation, we augment each dataset’s training split with the data from all other datasets. For instance, for ZSL on HMDB51 we augment the training data with all videos from UCF101 and Olympic Sports.

Compared Methods: We study the impact of the data augmentation methods: Naive DA: Naive Data Augmentation [9, 41] simply assigns equal weight to each auxiliary training sample. Visual KLIEP: The auxiliary data is aligned with the testing sample distribution $\mathbf {X}^{te}$ (Eq. (8)). Category KLIEP: The auxiliary categories are aligned with testing category distribution $\mathbf {Z}^{te}$. This is achieved by the same procedure in Eq. (8) by replacing $\mathbf {x}$ with $\mathbf {z}$. Full KLIEP: The distribution of both samples $\mathbf {X}^{te}$ and categories $\mathbf {Z}^{te}$ is used to reweight the auxiliary data (Eq. (12)).

Results: From the results in Table 3, we draw the conclusions: (i) Both the baseline single task learning (STL) method and our Multi-Task Embedding (MTE) improve with Naive DA (compare unaugmented results in Table 2), (ii) The Visual, Category, and Full visual+category-based weightings all improve on Naive DA in the case of STL RR. (iii) We see that our MTE with Full KLIEP augmentation performs the best overall. The ability of KLIEP to improve on Naive DA suggests that the auxiliary data is indeed of variable relevance to the target data, and selectively re-weighing the auxiliary data is important. (iv) For KLIEP-based DA, either Visual or Category DA provides most of the improvement, with relatively less improvement obtained by using both together.

Table 3. Data augmentation and importance weighting for ZSL action recognition.

Alternative Models. We also compare against previous state-of-the-art methods including those driven by both attributes and word-vector category embeddings. DAP/IAP [5]: Direct/Indirect attribute prediction are classic attribute-based zero-shot recognition models based on training SVM classifiers independently for each attribute, and using a probabilistic model to match attribute predictions with target classes. HAA: We implement a simplified version of the Human Actions by Attributes model [21]: We first train attribute detection SVMs, and test samples are assigned to categories based on cosine distance between their vector of attribute predictions and the target classes’ attribute vectors. SVE [9]: Support vector regression was adopted to learn the visual to semantic mapping. ESZSL [42]: Embarrassingly Simple Zero-Shot Learning defines the loss function as the mean square error on label prediction in contrast to the regression loss defined in other baseline models. SJE: Structured Joint Embedding [7] employed a triplet hinge loss. The objective is to enforce relevant labels having higher projection values from visual features than those of non-relevant labels. UDA: The Unsupervised Domain Adaptation model [22] learns dictionary on auxiliary data and adapts it to the target data as a constraint on the target dictionary rather than blindly using the same dictionary. This work combines both attribute and word vector embeddings.

Comparison Versus State of the Art: Table 4 compares our models with various contemporary and state-of-the-art models. For clear comparison, we indicate for each method which embedding ((W)ordvector/(A)ttribute) and feature (our FV, or BoW) are used, as well as whether it has a transductive dependency on the test data (TD) or exploits additional augmenting data (Aug). From these results we conclude that: (i) Although data augmentation has a big impact, our non-transductive and no data augmentation method (MTE) generally outperforms prior alternatives due to learning an effective latent matching space robust to the train/test class shift; (ii) The performance of our MTE with word-vector embedding is strong when compared with DAP/IAP/HAA/ESZSL even with attribute embedding. Given the same attribute embedding, MTE outperforms all state-of-the-art models due to the discovery of latent attributes from the original attribute space; (iii) Moreover, given importance weighting on auxiliary data, our method (MTE + Full KLIEP) with word-vector embedding performs the best overall – including against [9] which also exploits data augmentation; (iv) Finally, our method is synergistic to the post processing self-training approach [11] as well as the hubness strategies [12], which further explains the advantages of our approach (MTE + Full KLIEP + PP) over other methods.

Table 4. Comparison versus state of the art. Embed: Label embedding, Feat: Visual feature used, Aug: Data augmentation required? TD: Transductive Requirement?

Fig. 2.

Visualisation of Full KLIEP auxiliary data weighting. Left: 4 target videos with category names. Right: 16 auxiliary videos with bars indicating the estimated weights.

5.3 Qualitative Results and Further Analysis

Importance Weighting: To visualise the impact of our IW, we randomly select 4/16 classes as target/auxiliary sets respectively. We then estimate the weight on the 16 auxiliary video classes according to the Full KLIEP (Sect. 4). Examples of the auxiliary video weightings are presented in Fig. 2. We observe that auxiliary classes semantically related to the targets are given higher weight e.g. HandstandPushups$\,\rightarrow \,$Cartwheel in first sample, SalsaSpin$\,\rightarrow \,$Hug and Sword Exercise$\,\rightarrow \,$Fencing in the second sample. While the visually and semantically less relevant auxiliary videos are given much lower weights.

Multi-Task Embedding: We next qualitatively illustrate single versus multi-task visual-semantic mappings. Specifically we take 5 classes to be recognized and visualise their data after visual-semantic projection by tSNE [43]. A comparison between the representations generated by single-task (RR) and multi-task (MTE) mappings is given in Fig. 3. The multi-task embedding discovers data in a lower dimension latent space where NN classification becomes more meaningful. The improved representation is illustrated by computing the ROC curve for each target category, as seen in Fig. 3. MTE provides improved detection over RR, demonstrating the better generalisation of this representation.

Fig. 3.

Qualitative comparison between single-task ridge regression (RR) and multi-task embedding (MTE).

6 Conclusion

In this work, we focused on zero-shot action recognition from the perspective of improving generalisation of the visual-semantic mapping across the disjoint train/test class gap. We propose both model- and data-centric improvements to a traditional regression-based pipeline by respectively, multi-task embedding – to minimise overfit of the train data and to build a lower dimensional latent matching space; and prioritising data augmentation by importance weighting – to best exploit auxiliary data for the recognition of target categories. Our experiments on a set of contemporary action-recognition benchmarks demonstrate the impact of both our contributions and show state-of-the-art results overall.