Sparse Representation Based Complete Kernel Marginal Fisher Analysis Framework for Computational Art Painting Categorization

Abstract

This paper presents a sparse representation based complete kernel marginal Fisher analysis (SCMFA) framework for categorizing fine art images. First, we introduce several Fisher vector based features for feature extraction so as to extract and encode important discriminatory information of the painting image. Second, we propose a complete marginal Fisher analysis method so as to extract two kinds of discriminant information, regular and irregular. In particular, the regular discriminant features are extracted from the range space of the intraclass compactness using the marginal Fisher discriminant criterion whereas the irregular discriminant features are extracted from the null space of the intraclass compactness using the marginal interclass separability criterion. The motivation for extracting two kinds of discriminant information is that the traditional MFA method uses a PCA projection in the initial step that may discard the null space of the intraclass compactness which may contain useful discriminatory information. Finally, we learn a discriminative sparse representation model with the objective to integrate the representation criterion with the discriminant criterion in order to enhance the discriminative ability of the proposed method. The effectiveness of the proposed SCMFA method is assessed on the challenging Painting-91 dataset. Experimental results show that our proposed method is able to (i) achieve the state-of-the-art performance for painting artist and style classification, (ii) outperform other popular image descriptors and deep learning methods, (iii) improve upon the traditional MFA method as well as (iv) discover the artist and style influence to understand their connections in different art movement periods.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fine art painting categorization and analysis is an emerging research area in computer vision, which is gaining increasing popularity in the recent years. Pioneer works in cognitive psychology [1, 2] believe that the analysis of visual art is a complex cognitive task and requires involvement of multiple centers in the human brain in order to process different elements of visual art such as color, shapes, boundaries and brush strokes.

From the computer vision point of view, unlike conventional image classification tasks, computational painting categorization exhibits two important issues for artist classification and style classification respectively. First, as for the artist classification, there are large variations in appearance, topics and styles within the paintings of the same artist. Second, as for the style classification, the inherent similarity gap between paintings within the same style is much larger compared to other image classification tasks such as object recognition and face recognition where the images of the same class have a lower variance in similarity. Painting art images are different from photographic images due to the following reasons: (i) Texture, shape and color patterns of different visual classes in art images (say, a multicolored face or a disproportionate figure) are inconsistent with regular photographic images. (ii) Some artists have a very distinctive style of using specific colors (for ex: dark shades, light shades etc.) and brush strokes resulting in art images with diverse background and visual elements. As a result, conventional features, such as LBP [3], PHOG [4], GIST [5], SIFT [6], complete LBP [7], CN-SIFT [8] etc., which are applied to conventional image classification, independently cannot capture the key aspects of computational painting categorization. A comparative evaluation of different conventional features by Khan et al. [8] for computational fine art painting categorization clearly suggests the need of designing more powerful visual features and learning methods in order to effectively capture complex discriminative information from fine art painting images.

To address the issues raised above, we first present DAISY Fisher vector (D-FV), WLD-SIFT Fisher vector (WS-FV) and color fused Fisher vector (CFFV) features for feature extraction so as to encode the local, color, spatial, relative intensity and gradient orientation information. We then propose a complete marginal Fisher analysis method so as to overcome the limitation of the traditional marginal Fisher analysis (MFA) [9] method. The initial step of the traditional MFA method is the principal component analysis (PCA) projection which projects the data into the PCA subspace. A potential problem with the PCA step is that it may discard the null space of the intraclass compactness which may contain useful discriminatory information since the PCA criterion is not compatible with the MFA criterion. In our proposed method, we extract two kinds of discriminatory information, regular and irregular so as to overcome the drawback of the PCA projection step. Specifically, we extract the regular discriminant features from the range space of intraclass compactness using marginal Fisher discriminant criterion whereas the irregular discriminant features are extracted from its null space using the marginal interseparability criterion. Finally, we apply a discriminative sparse model by adding a discriminant term to the sparse representation criterion so as to have correspondence between the dictionary atoms and class labels for improving the pattern recognition performance. In particular, we utilize the intrinsic structure of sparse representation in order to define new discriminative within-class and between-class matrices for learning the discriminative dictionary efficiently using a discriminative sparse optimization criterion. Our proposed method is evaluated on the challenging Painting-91 dataset [8] and experimental results show that our framework achieves the state-of-the-art performance for fine art painting categorization, outperforms other popular image descriptors and deep learning methods and discover the artist influence and style influence.

The rest of this paper is organized as follows. In Sect. 2, we briefly review some related work on painting categorization, feature extraction and learning methods. In Sect. 3, we present the feature extraction step using the proposed Fisher vector features. Section 4 describes the motivation and theoretical formulation of the sparse representation based kernel MFA framework. Section 5 conducts extensive experiments and analysis of results. Finally, we conclude the paper in Sect. 6.

2 Related Work

Painting Categorization. Recently, several research efforts have been invested on developing techniques for fine art categorization using computer vision methods. Sablatnig et al. [10] examined the structural characteristics of a painting and introduced a classification scheme based on color, shape of region and structure of brush strokes in painting images. Shamir et al. [11] showed a method to automatically categorize paintings using low level features and find common elements between painters and artistic styles. A statistical model for combining multiple visual features was proposed by Shen [12] for automatic categorization of classical western paintings. Shamir and Tarakhovsky [13] presented an image analysis method inspired from cell biology for analysis of art painting based on painters, different artistic movements, artistic styles, and provide similar elements and influential links between painters. The work of Zujovic et al. [14] proposed an approach to classify paintings by analyzing different features in order to capture salient aspects of a painting. Siddique et al. [15] developed a framework for learning multiple kernels efficiently by greedily selecting data instances for each kernel using AdaBoost followed by SVM learning.

Feature Extraction. Local, color, spatial and intensity information are the cues based on which the visual cortex of the human brain can find discriminative elements in different images, and hence these cues are necessary for precise fine art painting categorization. Guo et al. [7] proposed a complete modeling of the local binary pattern descriptor to extract the image local gray level and the sign and magnitude features of local difference. The work of van de Sande et al. [16] showed the effectiveness of color invariant features for categorization tasks to increase the illumination invariance and the discriminative power. Shechtman and Irani [17] presented an approach to measure similarity between images using a self-similarity descriptor by capturing self-similarities of color, edges, repetitive patterns and complex textures.

Learning Methods. Several manifold learning methods such as marginal Fisher analysis (MFA) [9], locality preserving projections [18], locality sensitive discriminant analysis (LSDA) [19] etc. have been widely used to preserve data locality in the embedding space. The MFA method [9] proposed by Yan et al. overcomes the limitations of the traditional linear discriminant analysis method and uses a graph embedding framework for supervised dimensionality reduction. Cai et al. [19] proposed the LSDA method that discovers the local manifold structure by finding a projection which maximizes the margin between data points from different classes at each local area.

In visual recognition applications, sparse representation methods focus on developing efficient learning algorithms [20, 21] and exploring data manifold structures for representation [22, 23]. Zhou et al. [24] proposed a novel joint dictionary learning (JDL) algorithm to exploit the visual correlation within a group of visually similar object categories for dictionary learning. Mairal et al. [25] proposed to co-train the discriminative dictionary, sparse representation as well as the linear classifier using a combined objective function.

3 Feature Extraction Using Fused Fisher Vector Features

In this section, we present a set of image features that encode the local, color, spatial, relative intensity and gradient orientation information of fine art painting images.

3.1 Fisher Vector

We briefly review the Fisher vector which is widely applied for different visual recognition problems such as face detection and recognition [26], object classification [27, 28], etc. Theoretical analysis [27] shows that Fisher vector features describes an image by what makes it different from other images. In particular, let $\mathbf{X} = \{\mathbf{f}_t, t = 1,2,\ldots ,T \}$ be the set of T local descriptors extracted from the image, then the Fisher kernel is defined as: $K(\mathbf{X},\mathbf{Y}) = (\mathbf{G}_\lambda ^{X})^T \mathbf{F}_\lambda ^{-1} \mathbf{G}_\lambda ^{Y}$ where $\mu _\lambda$ is the probability density function of $\mathbf{X}$ with parameter $\lambda$ and $\mathbf{F}_\lambda$ is the Fisher information matrix of $\mu _\lambda$. The gradient vector of the log-likelihood that indicates the contribution of the parameters to the generation process can be represented as: $\mathbf{G}_\lambda ^X = \frac{1}{T} \bigtriangledown _\lambda \log _{\mu _\lambda } (\mathbf{X})$. Since $\mathbf{F}_\lambda ^{-1}$ is symmetric and positive definite, it has a Cholesky decomposition as $\mathbf{F}_\lambda ^{-1} = \mathbf{L}_\lambda ^T \mathbf{L}_\lambda$. Therefore, the kernel $K(\mathbf{X},\mathbf{Y})$ can be written as a dot product between normalized vectors $\mathbf{G}_\lambda$, obtained as $\mathbf{G}_\lambda ^X = \mathbf{L}_\lambda \mathbf{G}_\lambda ^X$ where $\mathbf{G}_\lambda ^X$ is the Fisher vector of X.

3.2 DAISY Fisher Vector (D-FV)

In this section, we present a DAISY Fisher vector (D-FV) feature where Fisher vectors are computed on densely sampled DAISY descriptors. DAISY descriptors consists of values computed from the convolved orientation maps located on concentric circles centered on each pixel location. The DAISY descriptor [29] $\mathcal {D}(u_0,v_0)$ for location $(u_0,v_0)$ is represented as:

$$\begin{aligned} \begin{aligned}&\mathcal {D}(u_0,v_0) = [ \tilde{\mathbf{h}}_{\varSigma _1}^T(u_0,v_0), \\&\tilde{\mathbf{h}}_{\varSigma _1}^T(\mathbf{I}_1(u_0,v_0,R_1)),\ldots ,\tilde{\mathbf{h}}_{\varSigma _1}^T(\mathbf{I}_T(u_0,v_0,R_1)),\ldots ,\\&\tilde{\mathbf{h}}_{\varSigma _Q}^T(\mathbf{I}_1(u_0,v_0,R_Q)),\ldots ,\tilde{\mathbf{h}}_{\varSigma _Q}^T(\mathbf{I}_T(u_0,v_0,R_Q)) ]^T \end{aligned} \end{aligned}$$

(1)

where $\mathbf{I}_j(u,v,R)$ is the location with distance R from (u, v) in the direction given by j, Q represents the number of circular layers and $\tilde{\mathbf{h}}_{\varSigma }(u,v)$ is the unit norm of vector containing $\varSigma$-convolved orientation maps in different directions. DAISY descriptors are suitable for dense computation and offers precise localization and rotational robustness, therefore provides improved performance and better accuracy for classification relative to other local descriptors such as GLOH, SURF and NCC [29]. We fit the sampled DAISY descriptors to a Gaussian Mixture Model (GMM) with 256 parameters and the GMM is trained for each component of the image separately in order to encode the color information. The Fisher vectors are then encoded as derivatives of log-likelihood of the model based on the parameters.

Fig. 1.

Framework of the feature extraction process.

3.3 Weber-SIFT Fisher Vector (WS-FV)

We introduce a Weber-SIFT Fisher vector (WS-FV) feature that integrates the Weber local descriptor along with SIFT features so as to encode the color, local, relative intensity and gradient orientation information from an image. The Weber local descriptor (WLD) [30] is based on the Weber’s law [31] which states that the ratio of increment threshold to the background intensity is a constant. The descriptor contains two components differential excitation [30] and orientation [30] which are defined as:

$$\begin{aligned} \begin{aligned}&\xi (x_c) = \arctan \left[ \frac{\nu _s^{00}}{\nu _s^{01}}\right] \; and \; \theta (x_c) = \arctan \left( \frac{\nu _s^{11}}{\nu _s^{10}}\right) \end{aligned} \end{aligned}$$

(2)

where $\xi (x_c)$ is the differential excitation and $\theta (x_c)$ is the orientation of the current pixel $x_c$, $x_i (i=0,1,...p-1)$ denotes the i-th neighbours of $x_c$ and p is the number of neighbors, $\nu _s^{00}$, $\nu _s^{01}$, $\nu _s^{10}$ and $\nu _s^{11}$ are the output of filters $f_{00}$, $f_{01}$, $f_{10}$ and $f_{11}$ respectively. The WLD descriptor is based on a biological model and its feature extraction process simulates how humans perceive the environment. WLD provides robustness to illumination changes and noise in the image [30], therefore acts as a good descriptor for painting images.

In order to encode important discriminatory information of the painting image, we compute the WLD for every component of the image to form the color WLD. SIFT features are then densely sampled and the process is repeated separately for the three components of the image resulting in color WLD-SIFT feature. We train a parametric model [32, 33], in our case, Gaussian Mixture Model (GMM) by fitting it to the sampled color WLD-SIFT features. The spatial information is also encoded by augmenting the visual features derived by SIFT with their spatial co-ordinates [34]. The Fisher vectors are then extracted by capturing the average first order and second order differences between the computed features and each of the GMM centers.

3.4 Color Fused Fisher Vector (CFFV)

In this section, we present a fused Fisher vector feature (FFV) that combines the most expressive features of the D-FV, WS-FV and SIFT-FV features. In the SIFT-FV feature, we compute Fisher vectors on densely sampled SIFT features using a GMM [26, 33] for every component of the image. The most expressive features are then extracted by means of principal component analysis (PCA) [35].

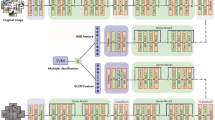
To derive the proposed FFV feature, we first compute the D-FV, WS-FV and the color SIFT-FV for all the components of the image separately. The D-FV features of R, G and B components of the image are concatenated and normalized to zero mean and unit standard deviation. The dimensionality of the D-FV feature is then reduced by using PCA, which derives the most expressive features with respect to the minimum square error. The above process is then repeated for the WS-FV and SIFT-FV features. Finally, the computed D-FV, WS-FV and the SIFT FV features are further concatenated and normalized to create the FFV feature. Figure 1 shows the component images, the process of computation of D-FV, WS-FV and the SIFT-FV features, the PCA process and the CFFV feature derived from the concatenation and subsequent normalization of the computed features. The color cue provides powerful discriminating information in pattern recognition in general [36, 37], therefore we also incorporate color information to our proposed feature. We repeat the above steps and compute the FFV in different color spaces namely YCbCr, YIQ, LAB, oRGB, XYZ, YUV and HSV. The CFFV feature is derived by fusing the FFV features in the different color spaces listed above.

4 Sparse Representation Based Complete Kernel Marginal Fisher Analysis Framework

In this section, we build a theoretical framework for sparse representation based complete kernel marginal Fisher analysis (SCMFA) based on two phase MFA framework. In SCMFA, we capture two kinds of important discriminant information namely the regular and irregular discriminant features from the range space and null space of intraclass compactness of the MFA method. We then use a discriminative sparse representation model with the objective of integrating representation criterion such as sparse coding with discriminative criterion so as to enhance the discriminative ability of the proposed method.

4.1 Motivation

The linear discriminant analysis (LDA) method assumes that the data of each class is of Gaussian distribution which is not always satisfied in real world problems. The separability of different classes cannot be well characterized by the interclass scatter if the above property is not satisfied [9]. This limitation of LDA is overcome by the marginal Fisher analysis (MFA) [9] which develops a new criteria that characterizes the intraclass compactness and interclass separability using an intrinsic and a penalty graph respectively.

Given the sample data matrix $\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_m] \in \mathbb {R}^{n \times m}$ that consists of m samples each with dimension n, the intraclass compactness is characterized from the intrinsic graph by the term

$$\begin{aligned} \begin{aligned}&\tilde{\mathbf{S}_{c}} = \sum _i \sum _{i \in N_{k_1}^{+}(j) or j \in N_{k_1}^{+}(i)} ||\mathbf{W}^{T} \mathbf{x}_i - \mathbf{W}^{T} \mathbf{x}_j||^{2} = 2\mathbf{W}^{T}{} \mathbf{X}(\mathbf{D} - \mathbf{A})\mathbf{X}^{T}{} \mathbf{W} \\ \end{aligned} \end{aligned}$$

(3)

where $\mathbf{A}_{ij}$ is 1 if $i \in N_{k_1}^{+}(j)$ or $j \in N_{k_1}^{+}(i)$ and 0 otherwise, $N_{k_1}^{+}(i)$ denotes the set of $k_1$ nearest neighbors of the sample $x_i$ of the same class. The interclass separability is characterized by the following penalty graph:

$$\begin{aligned} \begin{aligned}&\tilde{\mathbf{S}_{p}} = \sum _i \sum _{(i,j) \in P_{k_2}(c_i) or (i,j) \in P_{k_2}(c_j)} ||\mathbf{W}^{T} \mathbf{x}_i - \mathbf{W}^{T} \mathbf{x}_j||^{2} = 2\mathbf{W}^{T}{} \mathbf{X}(\mathbf{D}^p - \mathbf{A}^p)\mathbf{X}^{T}{} \mathbf{W} \\ \end{aligned} \end{aligned}$$

(4)

where $\mathbf{A}_{ij}^{p}$ is 1 if $(i,j) \in P_{k_2}(c_i)$ or $(i,j) \in P_{k_2}(c_j)$ and 0 otherwise, $P_{k_2}(c)$ denotes the set that are $k_2$ nearest neighbors among the set $\{ (i,j),i\in \pi _{c}, j\mathrel {\not \in }\pi _{c} \}$. As a result, the marginal Fisher criterion [9] is given as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{T} = \arg \max _W \frac{\mathbf{tr}(\mathbf{W}^{T}{} \mathbf{X}(\mathbf{D}^p - \mathbf{A}^p)\mathbf{X}^{T}{} \mathbf{W})}{\mathbf{tr}(\mathbf{W}^{T}{} \mathbf{X}(\mathbf{D} - \mathbf{A})\mathbf{X}^{T}{} \mathbf{W})} = \arg \max \frac{\mathbf{tr}(\tilde{\mathbf{S}_{p}})}{\mathbf{tr}(\tilde{\mathbf{S}_{c}})} \\ \end{aligned} \end{aligned}$$

(5)

The initial step of the MFA method is the PCA projection which projects the data into the PCA subspace where the dimensionality is reduced. A potential problem with the PCA step is that it may discard dimensions that contain important discriminative information as the PCA criterion is not compatible with the MFA criterion. Previous works of research by [38, 39] for the linear discriminant analysis method prove that the null space of the within-class scatter matrix contain important discriminative information whereas the null space of the between-class scatter matrix contain no useful discriminatory information. We apply the same motivation for the intraclass compactness and the interclass separability of the MFA method.

In the complete kernel marginal Fisher analysis method, the strategy is to split the intraclass compactness $\mathbf{S}_c^k$ into two subspaces namely the range space $\mathbf{C}_{r}$ and null space $\mathbf{C}_{n}$ so as to extract two kinds of discriminant features: regular and irregular discriminant features. The regular discriminant features are extracted from the range space using the marginal Fisher discriminant criterion whereas the irregular discriminant features are extracted from the null space using the marginal interclass separability criterion.

In our proposed method, the kernel trick is used so as to increase the separation ability. Specifically, we use the Fisher kernel [32] with the kernel function $\phi (\mathbf{x}): \mathbb {R}^{n} \rightarrow \mathbb {R}^{h}$ and $\mathbf{K}$ is the kernel gram matrix where $K_{ij} = K(x_i,x_j)$. The kernel marginal Fisher criterion is represented as:

$$\begin{aligned} \begin{aligned}&\mathbf{T}^{*} = \arg \max _{J} \frac{\mathbf{tr}( \mathbf{J}^{T}{} \mathbf{K}(\mathbf{D}^p - \mathbf{A}^p)\mathbf{K}^{T}{} \mathbf J )}{\mathbf{tr}( \mathbf J ^{T}{} \mathbf{K}(\mathbf D - \mathbf{A})\mathbf K ^{T}{} \mathbf{J} )} = \arg \max \frac{ \mathbf{tr}(\mathbf S _{p}^k ) }{ \mathbf{tr}(\mathbf S _{c}^k ) } \\ \end{aligned} \end{aligned}$$

(6)

4.2 Extraction of Regular and Irregular Discriminant Features

Suppose $\varvec{\beta }_1, \varvec{\beta }_2,...,\varvec{\beta }_h$ be the eigenvectors of $\mathbf{S}_c^k$ then we define the range space as $\mathbf{C}_r = [\varvec{\beta }_1,...,\varvec{\beta }_p]$ corresponding to the nonzero eigenvalues and the null space as $\mathbf{C}_n = [\varvec{\beta }_{p+1},...,\varvec{\beta }_h]$ where $p<h$. We extract the regular discriminant features from the range space of $\mathbf{S}_c^k$. As a result, the objective function is to maximize the marginal Fisher discriminant criterion which can be expressed as:

$$\begin{aligned} \begin{aligned}&\mathbf{T}^{r} = \arg \max \frac{ \mathbf{tr}( \mathbf C _r^{T} \mathbf{S}_{p}^{k} \mathbf{C}_r )}{ \mathbf{tr}( \mathbf C _r^{T} \mathbf{S}_{c}^{k} \mathbf{C}_r )} \\ \end{aligned} \end{aligned}$$

(7)

The criterion in Eq. (7) can be maximized directly by calculating the eigenvectors of the following eigen-equation:

$$\begin{aligned} \begin{aligned}&\mathbf{S}_{p}^{k} \mathbf{C}_r = \lambda \mathbf{S}_{c}^{k} \mathbf{C}_r \\ \end{aligned} \end{aligned}$$

(8)

Let $\varvec{\xi } = [\varvec{\xi }_1, \varvec{\xi }_2,\ldots , \varvec{\xi }_p]$ be the solutions of Eq. 8 ordered according to their eigenvalues, then the regular discriminant features are given as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{U}^{r} = \varvec{\xi }^{T} \mathbf{C}_r^T \mathbf K \\ \end{aligned} \end{aligned}$$

(9)

In order to compute the irregular discriminant features, the strategy is to remove the null space of interclass separability $\mathbf{S}_p^k$ and keep the null space of intraclass compactness $\mathbf{S}_c^k$. The null space of $\mathbf{S}_c^k$ is defined above as: $\mathbf{C}_n = [\varvec{\beta }_{p+1},....,\varvec{\beta }_h]$. We will diagonalize the $\mathbf{S}_p^k$ in the null space of $\mathbf{S}_c^k$ so as to project the data to the null space of $\mathbf{S}_c^k$.

$$\begin{aligned} \begin{aligned}&\hat{ \mathbf{S}_{p}^{k} } = \mathbf{C}_n^{T} \mathbf{S}_{p}^{k} \mathbf{C}_n \\ \end{aligned} \end{aligned}$$

(10)

As a result, the objective function is to maximize the marginal interclass separability criterion which can be expressed as:

$$\begin{aligned} \begin{aligned}&\mathbf{T}^{ir} = \arg \max \mathbf{tr}( \mathbf C _n^{T} \mathbf{S}_{p}^{k} \mathbf{C}_n ) = \arg \max \mathbf{tr}( \hat{ \mathbf{S}_{p}^{k} } )\\ \end{aligned} \end{aligned}$$

(11)

We then have to remove the null space of $\hat{\mathbf{S}_p^k}$ since it has no useful discriminatory information. We maximize the criterion in Eq. 11 by eigenvalue analysis. Let $\zeta = [\zeta _1,\ldots ,\zeta _{h-p}]$ be the eigen vectors ordered according to their eigenvalues, then we select $\zeta _{ir} = [\zeta _1,\ldots ,\zeta _{l}]$ corresponding to the nonzero eigenvalues where $l<(h-p)$. Therefore, we define the irregular discriminant features as:

$$\begin{aligned} \begin{aligned}&\mathbf{U}^{ir} = \varvec{\zeta }_{ir}^{T} \mathbf{C}_n^T \mathbf K \\ \end{aligned} \end{aligned}$$

(12)

In order to obtain the final set of features, the regular and irregular discriminant features are fused and normalized to zero mean and unit standard deviation.

$$\begin{aligned} \begin{aligned}&\mathbf{U} = \begin{bmatrix} \mathbf{U}^{r}\\ \mathbf{U}^{ir} \end{bmatrix} \\ \end{aligned} \end{aligned}$$

(13)

4.3 Discriminative Sparse Representation Model

In this section, we use a discriminative sparse representation criterion with the rationale to integrate the representation criterion such as sparse coding with the discriminative criterion so as to improve the classification performance. Given the feature matrix $\mathbf{U} = [\mathbf u _1, \mathbf{u}_2,\ldots ,\mathbf{u}_l] \in \mathbb {R}^{l \times m}$ learned from the complete marginal Fisher analysis method, which contains m samples in a l dimensional space, let $\mathbf{D} = [\mathbf d _1, \mathbf{d}_2,\ldots ,\mathbf{d}_r] \in \mathbb {R}^{l \times m}$ denote the dictionary that represents r basis vectors and $\mathbf{S} = [\mathbf s _1, \mathbf{s}_2,\ldots ,\mathbf{s}_m] \in \mathbb {R}^{r \times m}$ denote the sparse representation matrix which represents the sparse representation for m samples. Each coefficient $\mathbf{a}_i$ correspond to the items in the dictionary $\mathbf{D}$.

In our proposed discriminative sparse representation model, we optimize a sparse representation criterion and a discriminative analysis criterion to derive the dictionary $\mathbf{D}$ and sparse representation $\mathbf{S}$ from the training samples. We use the representation criterion of the sparse representation to define new discriminative within-class matrix $\hat{\mathbf{H}_w}$ and discriminative between-class matrix $\hat{\mathbf{H}_b}$ by considering only the k nearest neighbors. Specifically, using the sparse representation criterion the descriminative within class matrix is defined as $\hat{\mathbf{H}_w} = \sum _{i=1}^{m} \sum _{(i,j) \in N_k^w(i,j) } (\mathbf{s}_i - \mathbf s _j)(\mathbf{s}_i - \mathbf s _j)^{T}$, where $(i,j) \in N_k^w(i,j)$ represents the (i, j) pairs where sample $\mathbf{u}_i$ is among the k nearest neighbors of sample $\mathbf{u}_j$ of the same class or vice versa. The discriminative between class matrix is defined as $\hat{\mathbf{H}_b} = \sum _{i=1}^{m} \sum _{(i,j) \in N_k^b(i,j) } (\mathbf{s}_i - \mathbf s _j)(\mathbf{s}_i - \mathbf s _j)^{T}$, where $(i,j) \in N_k^b(i,j)$ represents k nearest (i, j) pairs among all the (i, j) pairs between samples $\mathbf{u}_i$ and $\mathbf{u}_j$ of different classes.

As a result, we define the new optimization criterion as:

$$\begin{aligned} \begin{aligned}&\min _{ \mathbf{D},\mathbf S } \sum _{i=1}^{m} \{ ||\mathbf{u}_i - \mathbf D {} \mathbf{s}_i||^{2} + \lambda ||\mathbf{s}_i||_{1} \} + \alpha \mathbf{tr}( \beta \hat{\mathbf{H}_w} - (1-\beta ) \hat{\mathbf{H}_b} ) \\&s.t. ||\mathbf{d}_j|| \le 1, (j=1, 2,\ldots , r)\\ \end{aligned} \end{aligned}$$

(14)

where the parameter $\lambda$ controls the sparseness term, the parameter $\alpha$ controls the discriminatory term, the parameter $\beta$ balances the contributions of the discriminative within class matrix $\hat{\mathbf{H}_w}$ and between class matrix $\hat{\mathbf{H}_b}$ and $\mathbf{tr(.)}$ denotes the trace of a matrix.

In order to derive the discriminative sparse representation for the test data, as the dictionary $\mathbf{D}$ is already learned, we only need to optimize the following criterion: $\min _{B} \sum _{i=1}^{t} \{ ||\mathbf{y}_i - \mathbf D {} \mathbf{b}_i ||^2 \} + \lambda ||\mathbf{b}_i||_1$ where $\mathbf{y}_1, \mathbf y _2,\ldots , \mathbf{y}_t$ are the test samples and t is the number of test samples. The discriminative sparse representation for the test data is defined as $\mathbf{B} = [\mathbf b _1,\ldots , \mathbf{b}_t] \in \mathbb {R}^{r \times t}$. Since the dictionary $\mathbf{D}$ is learned from the training optimization process, it contains both sparseness and discriminative information, therefore the derived representation $\mathbf{B}$ is the discriminative sparse representation for the test set.

5 Experiments

In this section, we evaluate the performance of our proposed method for fine art painting categorization using the challenging Painting-91 dataset [8]. There are 4266 painting images by 91 artists in the dataset covering different eras ranging from the early renaissance period to the modern art period. The images are collected from the internet and every artist has atleast 31 images. The dataset classifies 50 painters to 13 style categories with style labels as follows: abstract expressionism (1), baroque (2), constructivism (3), cubbism (4), impressionism (5), neoclassical (6), popart (7), post-impressionism (8), realism (9), renaissance (10), romanticism (11), surrealism (12) and symbolism (13).

5.1 Artist Classification

In this section, we make a comparative assessment of our proposed method with other popular image descriptors and deep learning methods on the task of artist classification. Artist classification is the task wherein we determine the artist for a painting. In order to follow the experimental protocol and have a fair comparison with other methods, we use the fixed train/test split provided in the dataset containing 2275 training and 1991 test images. MSCNN is the abbreviation for multi-scale convolutional neural networks. Experimental results in Table 1 show that our proposed SCMFA method achieves the state-of-the-art classification performance of 65.78 % for artist classification and outperforms other popular image descriptors and deep learning methods.

Table 1. Comparison of the proposed SCMFA method with other popular image descriptors and deep learning methods on the Painting-91 dataset.

Table 2. Art movement associated with different art styles.

5.2 Style Classification

In this section, we evaluate our proposed method on style classification wherein a painting is classified to its respective style out of the thirteen style categories defined in the dataset. The fourth column in Table 1 shows the results obtained using different features and learning methods for style classification. The experimental results demonstrate that our proposed SCMFA method achieves the state-of-the-art results compared to other popular image descriptors and deep learning methods for style classification.

Fig. 2.

The confusion matrix for 13 style categories of the Painting-91 dataset.

Figure 2 shows the confusion matrix for the style categorization where the rows show the true style categories and the columns show the assigned categories. It can be seen from Fig. 2 that style categories 1 (abstract expressionism), 13 (symbolism), 4 (cubbism) and 8(post-impressionism) give the best accuracy with classification rates of 93 %, 89 %, 81 % and 80 % respectively. The style category with the lowest accuracy is category 6 (neoclassical) as there are large confusions between the style categories baroque : neoclassical and renaissance : neoclassical. Similarly, the other style category pair that have large similarities is style renaissance : baroque due to evolution of the baroque style from the renaissance style.

5.3 Comprehensive Analysis of Results

We now evaluate the relation between the art painting styles and the art movement periods. An art movement period is a movement wherein a group of artists follow a common philosophy or goal in art during a specific period of time. Table 2 shows the different art styles that were practiced in different art movement periods. Important patterns can be deduced by correlating the confusion diagram in Fig. 2 and the results of Table 2. We can observe that the art styles practiced in the same art movement period show higher similarity compared to art styles between different art movement periods. It can be seen from Fig. 2 that the style baroque has large confusions with styles neoclassical, romanticism and realism. These style categories belong to the same art movement period - post renaissance. Similarly, popart paintings have high similarities with styles surrealism and post impressionism within the same art movement period - modern art. The only exception to the above observation is the style categories renaissance and baroque as even though they belong to different art movement period, there are large confusions between them. The renaissance and baroque art paintings have high similarity as the baroque style evolved from the renaissance style resulting in few discriminating aspects between them [43].

Table 3. Comparison of the proposed method with marginal Fisher analysis method.

5.4 Comparison with the MFA Method

In this section, we compare our proposed SCMFA method with the traditional marginal Fisher analysis (MFA) method. In order to have a fair comparison, the same experimental settings and Fisher vectors features are used for comparison. The MFA uses a PCA projection in the initial step due to which important discriminatory information in the null space of intraclass compactness is lost. Our proposed SCMFA method overcomes this limitation by extracting two kinds of features, regular and irregular. Experimental results in Table 3 demonstrate that our proposed SCMFA method outperforms the MFA method.

5.5 Artist Influence

In this section, we analyze the artist influence which may help us link different artists that belong to an art movement period and also find relations between different art movement periods. The artist influence is determined by computing the correlation score of every artist in order to find similar elements between the paintings of different artists. In order to calculate the correlation score, we find the average of feature vector of all paintings by an artist. In particular, let $\mathbf{F}_{p}$ denote the average feature vector of all painting images by artist p. We then find the relation between the average feature vector of all artists by computing the correlation matrix. Finally, different artists are grouped together to form clusters based on the correlation score. Figure 3(a) shows the artist influence cluster graph with correlation threshold of 0.70.

Interesting observations can be deduced from Fig. 3(a). A particular art style and time period can be associated with every cluster. Cluster 1 shows artists with major contributions to the styles realism and romanticism and they belong to the post renaissance art movement period. Cluster 2 has the largest number of artists associated with the styles renaissance and baroque. Cluster 3 represents artists for the style Italian renaissance that took place in the $16^{th}$ century. And cluster 4 shows artists associated with style abstract expressionism in the modern art movement period.

5.6 Style Influence

In this section, we study the style influence so as to find common elements between different art styles and understand the evolution of art styles in different art movement periods. In order to calculate the style influence, we compute the average feature vector of all paintings for a style similar to the artist influence. The k-means clustering method is then applied with k set as 3 so as to form clusters of similar art styles. We finally plot a style influence graph using the first two principal components of the average feature vector.

Fig. 3.

(a) Shows the artist influence graph (b) shows the style influence graph.

Figure 3(b) shows the style influence graph clusters with k set as 3. Cluster 1 contains the styles of the post renaissance art movement period with the only exception of style renaissance. The reason for this may be due the high similarity between styles baroque and renaissance as the style baroque evolved from the style renaissance [43]. The styles impressionism, post impressionism and symbolism in cluster 2 show that there are high similarities between these styles in the modern art movement period as the three styles have a common french and belgian origin. Similarly, styles constructivism and popart in cluster 3 show high similarity in the style influence cluster graph.

6 Conclusion

This paper presents a sparse representation based complete kernel marginal Fisher analysis (SCMFA) framework for categorizing fine art painting images. First, we perform hybrid feature extraction by introducing the D-FV, WS-FV and CFFV features to extract and encode important discriminatory information of the art painting images. We then propose a complete marginal Fisher analysis method so as to extract regular and irregular discriminant features in order to overcome the limitation of the traditional MFA method. The regular features are extracted from the range space of the intraclass compactness whereas the irregular features are extracted from the null space of the intraclass compactness. Finally, we learn a sparse representation model so as to integrate the representation criterion with the discriminative criterion. Experimental results show that our proposed method outperforms other popular methods in the artist and style classification task of the challenging Painting-91 dataset.