Abstract
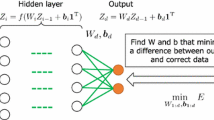
The backpropagation algorithm for calculating gradients has been widely used in computation of weights for deep neural networks (DNNs). This method requires derivatives of objective functions and has some difficulties finding appropriate parameters such as learning rate. In this paper, we propose a novel approach for computing weight matrices of fully-connected DNNs by using two types of semi-nonnegative matrix factorizations (semi-NMFs). In this method, optimization processes are performed by calculating weight matrices alternately, and backpropagation (BP) is not used. We also present a method to calculate stacked autoencoder using a NMF. The output results of the autoencoder are used as pre-training data for DNNs. The experimental results show that our method using three types of NMFs attains similar error rates to the conventional DNNs with BP.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bengio, Y., Lamblin, P., Popovici, D., Larochelle, H.: Greedy layer-wise training of deep networks. In: Proceedings of Advances in Neural Information Processing Systems, vol. 19, pp. 153–160 (2006)
Ciresan, D.C., Meier, U., Masci, J., Gambardella, L.M., Schmidhuber, J.: Flexible, high performance convolutional neural networks for image classification. In: Proceedings of 22nd International Joint Conference on Artificial Intelligence, pp. 1237–1242 (2011)
Chorowski, J., Member, S.: Learning understandable neural networks with non-negative weight constraints. IEEE Trans. Neural Netw. Learn. Syst. 26, 62–69 (2015)
Ding, D., Li, T., Jordan, M.I.: Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 32, 45–55 (2010)
Glorot, X., Bengio, Y.: Understanding the difficulty of training deep feedforward neural networks. In: International Conference on Artificial Intelligence and Statistics, pp. 249–256 (2010)
Glorot, X., Bordes, A., Bengio., Y.: Deep sparse rectifier neural networks. In: Proceedings of 14th International Conference on Artificial Intelligence and Statistics, pp. 315–323 (2011)
Hinton, G.E., Deng, L., Yu, D., Dahl, G.E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V.: Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Process. Mag. 29, 82–97 (2012)
Kingma, D.P., Ba, J.: ADAM: a method for stochastic optimization. In: The International Conference on Learning Representations (ICLR), San Diego (2015)
Krizhevsky, A., Hinton, G.: Learning multiple layers of features from tiny images. Technical report, Computer Science Department, University of Toronto, vol. 1, p. 7 (2009)
LeCun, Y.: The MNIST database of handwritten digits. http://yann.lecun.com/exdb/mnist
Lee, D.D., Seung, H.S.: Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791 (1999)
LeCun, Y., Bottou, L., Bengio, Y., Huffier, P.: Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998)
Nair, V., Hinton, G.E.: Rectified linear units improve restricted Boltzmann machines. In: Proceedings of ICML (2010)
Paatero, P., Tapper, U.: Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 5, 111–126 (1994)
Rumelhart, D.E., Hinton, G.E., Williams, R.J.: Learning representations by back-propagating errors. Nature 323, 533–536 (1986)
Srivastava, N., Hinton, G.E., Krizhevsky, A., Sutskever, I., Salakhutdinov, R.: Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958 (2014)
TensorFlow. https://www.tensorflow.org/
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Sakurai, T., Imakura, A., Inoue, Y., Futamura, Y. (2016). Alternating Optimization Method Based on Nonnegative Matrix Factorizations for Deep Neural Networks. In: Hirose, A., Ozawa, S., Doya, K., Ikeda, K., Lee, M., Liu, D. (eds) Neural Information Processing. ICONIP 2016. Lecture Notes in Computer Science(), vol 9950. Springer, Cham. https://doi.org/10.1007/978-3-319-46681-1_43
Download citation
DOI: https://doi.org/10.1007/978-3-319-46681-1_43
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46680-4
Online ISBN: 978-3-319-46681-1
eBook Packages: Computer ScienceComputer Science (R0)