Robust Cancer Treatment Outcome Prediction Dealing with Small-Sized and Imbalanced Data from FDG-PET Images

Abstract

Accurately predicting the outcome of cancer therapy is valuable for tailoring and adapting treatment planning. To this end, features extracted from multi-sources of information (e.g., radiomics and clinical characteristics) are potentially profitable. While it is of great interest to select the most informative features from all available ones, small-sized and imbalanced dataset, as often encountered in the medical domain, is a crucial challenge hindering reliable and stable subset selection. We propose a prediction system primarily using radiomic features extracted from FDG-PET images. It incorporates a feature selection method based on Dempster-Shafer theory, a powerful tool for modeling and reasoning with uncertain and/or imprecise information. Utilizing a data rebalancing procedure and specified prior knowledge to enhance the reliability and robustness of selected feature subsets, the proposed method aims to reduce the imprecision and overlaps between different classes in the selected feature subspace, thus finally improving the prediction accuracy. It has been evaluated by two clinical datasets, showing good performance.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Accurate outcome prediction prior to or even during cancer therapy is of great clinical value. It benefits the adaptation of more effective treatment planning for individual patient. With the advances in medical imaging technology, radiomics [1], referring to the extraction and analysis of a large amount of quantitative image features, provides an unprecedented opportunity to improve personalized treatment assessment. Positron emission tomography (PET), with the radio-tracer fluoro-2-deoxy-D-glucose (FDG), is one of the important and advanced imaging tools generally used in clinical oncology for diagnosis and staging. The functional information provided by FDG-PETs has also emerged to be predictive of the pathologic response of a treatment in some types of cancers, such as lung and esophageal tumors [10]. Abounding radiomic features have been studied in FDG-PETs [3], which include standardized uptake values (SUVs), e.g., SUV$_{max}$, SUV$_{peak}$ and SUV$_{mean}$, to describe metabolic uptakes in a volume of interest (VOI), and metabolic tumor volume (MTV) and total lesion glycolysis (TLG) to describe metabolic tumor burdens. Apart from SUV-based features, some complementary characterization of PET images, e.g., texture analysis, may also provide supplementary knowledge associated with the treatment outcome. Although the quantification of these radiomic features has been claimed to have discriminant power [1], the solid application is still hampered by some practical difficulties: (i) uncertainty and inaccuracy of extracted radiomic features caused by noise and limited resolution of imaging systems, by the effect of small tumour volumes, and also by the lack of a priori knowledge regarding the most discriminant features; (ii) small-sized dataset often encountered in the medical domain, which results in a high risk of over-fitting with a relatively high-dimensional feature space; (iii) skewed dataset where training samples are originated from classes of remarkably distinct sizes, thus usually leading to poor performance for classifying the minority class.

The challenge is to robustly select an informative feature subset from uncertain, small-sized, and imbalanced dataset. To learn efficiently from noisy and high overlapped training set, Lian et al. proposed a robust feature subset selection method, i.e., EFS [11], based on the Dempster-Shafer Theory (DST) [13], a powerful tool for modeling and reasoning with uncertain and/or imprecise knowledge. EFS quantifies the uncertainty and imprecision caused by different feature subsets; then, attempts to find a feature subset leading to both high classification accuracy and small overlaps between different classes. While it has shown competitive performance as compared to conventional methods, the influence of imbalanced data is still left unsolved; moreover, the loss function used in EFS can also be improved to reduce method’s complexity.

Fig. 1.

Protocol of the prediction system.

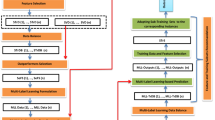
We propose a new framework for predicting the outcome of cancer therapy. Input features are extracted from multi-sources of information, which include radiomics in FDG-PET images, and clinical characteristics. Then, as a main contribution of this paper, EFS proposed in [11] is comprehensively improved to select features from uncertain, small-sized, and imbalanced dataset. The protocol of the proposed prediction system is shown in Fig. 1, which will be described in more detail in upcoming sections.

2 Robust Outcome Prediction with FDG-PET Images

The prediction system is learnt on a dataset $\{(X_i,Y_i)\}_{i=1}^n$ for N different patients, where vector $X_i$ consists of V input features, while $Y_i$ denotes already known treatment outcome. Since $Y_i$ in our applications only has two possibilities (e.g., recurrence versus no-recurrence), the set of possible classes is defined as $\varOmega =\{\omega _1,\omega _2\}$. It is worth noting that this prediction system can also deal with multi-class problems.

2.1 Feature Extraction

To extract features, images acquired at different time points are registered to the image at initial staging via a rigid registration method. The VOIs around tumors are cuboid bounding boxes manually delineated by experienced physicians. Five types of SUV-based features are calculated from the VOI, namely SUV$_{min}$, SUV$_{max}$, SUV$_{peak}$, MTV and TLG. To characterize tumor uptake heterogeneity, the Gray Level Size Zone Matrix (GLSZM) [16] is adopted to extract eleven texture features. Since the temporal changes of these features may also provide discriminant value, their relative difference between the baseline and the follow-up PET acquisitions is calculated as additional features. Patients’ clinical characteristics can also be included as complementary knowledge if they are available. The number of extracted features is roughly between thirty to fifty.

2.2 Feature Selection

In this part, EFS [11] is comprehensively improved, which is denoted as REFS for simplicity. As compared to EFS, REFS incorporates a data rebalancing procedure and specified prior knowledge to enhance the robustness of selected features on small-sized and imbalanced data. Moreover, to reduce method’s complexity, the loss function used in EFS is simplified without loss of effectiveness.

$\underline{\mathbf{Prior\;Knowledge: }}$ considering that SUV-based features have shown great significance for assessing the response of treatment [12], we incorporate this prior knowledge in REFS to guide feature selection. More specifically, RELIEF [9] is used to rank all SUV-based features. Then, the top SUV-based feature is included in REFS as a must be selected element of the desired feature subset. This added constraint drives REFS into a confined searching space. By decreasing the uncertainty caused by the scarcity of learning samples, it ensures more robust feature selection on small-sized datasets, thus increasing prediction reliability.

$\underline{\mathbf{Data\;Rebalancing: }}$ pre-sampling is a common approach for imbalanced learning [8]. As an effective pre-sampling method which can generate artificial minority class samples, adaptive synthetic sampling (ADASYN) [8] is adopted in REFS to rebalance data for feature selection. Such as the example shown in Fig. 2, the key idea of ADASYN is to adaptively simulate samples according to the distribution of the minority class samples, where more instances are generated for the minority class samples that have higher difficulty in learning.

Fig. 2.

Data rebalancing by ADASYN: (a) original data with two input features randomly selected from the lung tumor dataset (Sect. 3); (b) and (c) are two independent simulations, where more synthetic (yellow) instances have been generated for the minority class (cyan) samples which have higher difficulty in learning (on the boundary). However, due to the random nature, no points has been generated for minority class samples within the orange circle in (b).

However, due to the random nature of the rebalancing procedure, and also with a limited number of training samples, the rebalanced dataset can not always ensure that instances hard to learn are properly tackled (e.g., Fig. 2 (b)). Therefore, ADASYN is totally executed B (equals 5 in our experiment) times to provide B rebalanced training datasets. REFS is then executed with them to obtain B feature subsets. The final output is determined as the most frequently subset that occurred among the B independent actions.

$\underline{\mathbf{Robust\;EFS\;(REFS): }}$ similar to [11], we search for a qualified feature subset according to three requirements: (i) high classification accuracy; (ii) low imprecision and uncertainty, i.e., small overlaps between different classes; (iii) sparsity to reduce the risk of over-fitting. To learn such a feature subset, the dissimilarity between any feature vectors $X_i$ and $X_j$ is defined as a weighted Euclidean distance, i.e., $d^2_{i,j} = \sum _{p=1}^{V}\lambda _p d^2_{ij,p}$, where $d_{ij,p} = |x_{i,p}-x_{j,p}|$ represents the difference between the pth feature. Features are selected via the value of the binary vector $\varLambda = [\lambda _1,\ldots ,\lambda _V]^{t}$, where the pth feature is selected when $\lambda _p=1$.

We successively regard each training instance $X_i$ as a query object. In the framework of DST, other samples in the training pool can be considered as independent items of evidence that support different hypotheses regarding the class membership of $X_i$. The evidence offered by $(X_j,Y_j=\omega _q)$, where $j\ne i$ and $q\in \{1,2\}$, asserts that $X_i$ also belongs to $\omega _q$. According to [11], this piece of evidence is partially reliable, which can be quantified as a mass function [13], i.e., $m_{i,j}(\{\omega _q\})+m_{i,j}(\varOmega )=1$, where $m_{i,j}(\{\omega _q\})=\exp \left( -\gamma _q d_{i,j}^2\right)$, and $\gamma _q$ relates to the mean distance in the same class. Quantity $m_{i,j}(\{\omega _q\})$ denotes a degree of belief attached to the hypothesis “$Y_i \in \{\omega _q\}$”; similarly, $m_{i,j}(\varOmega )$ is attached to “$Y_i \in \varOmega$”, i.e., the degree of ignorance. The precision of $m_{i,j}$ is inversely proportional to $d^2_{i,j}$: when $d^2_{i,j}$ is too large, it becomes totally ignorant (i.e., $m_{i,j}(\varOmega )\approx 1$), which provides little evidence regarding the class membership of $X_i$. Hence, for each $X_i$, it is sufficient to just consider the mass functions offered by the first K (with a large value, e.g., $\ge 10$) nearest neighbors. Let $\{X_{i_1},\ldots ,X_{i_K}\}$ be the selected training samples for $X_i$. Correspondingly, $\{m_{i,i_1},\dots ,m_{i,i_K}\}$ are K pieces of evidence taking into account.

In the framework of DST, beliefs are refined by aggregating different items of evidence. A specific combination rule has been proposed in [11] to fuse mass functions $\{m_{i,i_1},\dots ,m_{i,i_K}\}$ for $X_i$. While it can lead to robust quantification of data uncertainty and imprecision, accompanying tuning parameters increase method’s complexity. To tackle this problem, this combination rule is replaced by the conjunctive combination rule defined in the Transferable Belief Model (TBM) [14], considering that the latter is a basic but robust rule for the fusion of independent pieces of evidence. We assign $\{m_{i,i_1},\dots ,m_{i,i_K}\}$ into two different groups ($\varTheta _1$ and $\varTheta _2$) according to $\{Y_{i_1},\ldots ,Y_{i_K}\}$. In each group $\varTheta _q\ne \emptyset$, mass functions are fused to deduce a new mass function $m_i^{\varTheta _q}$ without conflict:

$$\begin{aligned} {\left\{ \begin{array}{ll} m_i^{\varTheta _q}(\{\omega _q\}) &{} = 1-\prod ^{p=1,\ldots ,K}_{X_{i_p}\in \varTheta _q} \left( 1-e^{-\gamma _q d_{i,i_p}^2}\right) , \\ m_i^{\varTheta _q}(\varOmega ) &{} = \prod ^{p=1,\ldots ,K}_{X_{i_p}\in \varTheta _q} \left( 1-e^{-\gamma _q d_{i,i_p}^2}\right) ; \end{array}\right. } \end{aligned}$$

(1)

while, when $\varTheta _q$ is empty, $m_i^{\varTheta _q}(\varOmega )=1$. After that, $m_i^{\varTheta _1}$ and $m_i^{\varTheta _2}$ are further combined to obtain a global $M_i$ regarding the class membership of $X_i$, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} M_i(\{\omega _q\}) &{} = m_i^{\varTheta _q}(\{\omega _q\})\cdot m_i^{\varTheta _{\bar{q}}}(\varOmega ),\forall q\in \{1,2\}, \bar{q}\ne q,\\ M_i(\varOmega ) &{} = m_i^{\varTheta _1}(\varOmega )\cdot m_i^{\varTheta _2}(\varOmega ), \\ M_i(\emptyset ) &{} = m_i^{\varTheta _1}(\{\omega _1\})\cdot m_i^{\varTheta _2}(\{\omega _2\}). \end{array}\right. } \end{aligned}$$

(2)

Based on (1) and (2), $M_i$ is determined by the weighted Euclidean distance, i.e., a function of the binary vector $\varLambda$ defining which features are selected. Quantity $M_i(\emptyset )$ measures the conflict in the neighborhood of $X_i$. A large $M_i(\emptyset )$ means $X_i$ is locating in a high overlapped area in current feature subspace. Differently, $M_i(\varOmega )$ measures the imprecision regarding the class membership of $X_i$. A large $M_i(\varOmega )$ may indicate that $X_i$ is isolated from all other samples. According to the requirements of a qualified feature subset, the loss function with respect to $\varLambda$ is

$$\begin{aligned} \arg \min _{\varLambda } \frac{1}{N}\sum _{i=1}^{N}\sum _{q=1}^{2}\left\{ M_i(\{\omega _q\})-t_{i,q}\right\} ^2+\frac{1}{N}\sum _{i=1}^{N} \{{M_i(\emptyset )}^2+{M_i(\varOmega )}^2\}+\beta ||\varLambda ||_{0}. \end{aligned}$$

(3)

The first term is a mean squared error measure, where vector $t_i$ is a indicator of the outcome label, with $t_{i,q}=\delta _{i,q}$ if $Y_i=\omega _q$. The second term penalizes feature subsets that result in high imprecision and large overlaps between different classes. The last term, namely $||\varLambda ||_0=\sum _{v=1}^{V}\lambda _v$, forces the selected feature subset to be sparse. Scalar $\beta$ ($\ge 0$) is a hyper-parameter that controls the sparse penalty. It can be tuned according to the training performance. A global optimization method, namely the MI-LXPM [4], is utilized to minimize this loss function.

Finally, selected features are used to train a robust classifier, namely the EK-NN classification rule [5], for predicting the outcome of cancer treatment.

3 Experimental Results

The proposed prediction system has been evaluated by two clinical datasets:

• (1) Lung Tumor Data: twenty-five patients with inoperable stage II-III non-small cell lung cancer (NSCLC) treated with curative-intent chemo-radiotherapy were studied. All patients underwent FDG-PET scans at initial staging, after induction chemotherapy, and during the fifth week of radiotherapy. Totally 52 SUV-based and GLSZM-based features were extracted. At one year after the end of treatment, local or distant recurrence (majority) was diagnosed on 19 patients, while no recurrence (minority) was reported on the remaining 6 patients.

• (2) Esophageal Tumor Data: thirty-six patients with esophageal squamous cell carcinomas treated with chemo-radiotherapy were studied. Since only PET/CT scans at initial tumor staging were available, some clinical characteristics were included as complementary knowledge. As the result, 29 SUV-based, GLSZM-based, and patients’ clinical characteristics (gender, tumour stage and location, WHO performance status, dysphagia grade and weight loss from baseline) were gathered. At least one month after the treatment, 13 patients were labeled disease-free (minority) when neither loco regional nor distant tumor recurrence is detected, while the other 23 patients were disease-positive (majority).

Table 1. Feature selection and corresponding prediction performance evaluated by the .632+ Bootstrapping. “All” denotes the input feature space.

Fig. 3.

Evaluating REFS, where REFS$^+$ denotes resutls obtained without data rebalancing; while, REFS$^*$ denotes no prior knowledge.

Fig. 4.

Feature selected on (a) lung and (b) esophageal tumor datasets, respectively. Each column represents a bootstrapping evaluation, while the yellow points denote selected features.

$\underline{\mathbf{Feature\;Selection\; \& \;Prediction\;Performance: }}$ REFS was compared with two univariate methods (RELIEF [9] and FAST [2]), and four multivariate methods (SVMRFE [7], KCS [18], HFS [12] and EFS [11]). Because of a limited number of instances, all compared methods were evaluated by the .632+ Bootstrapping [6], which ensures low bias and variance estimation. As a metric used to evaluate the selection performance, the robustness of the selected feature subsets was measured by the relative weighted consistency [15]. Its calculation is based on feature occurrence statistics obtained from all iterations of the .632+ Bootstrapping. The value of the relative weighted consistency ranges between [0, 1], where 1 means all selected feature subsets are approximately identical. To assess the prediction performance after feature selection, Accuracy and AUC were calculated. For all the compared methods except EFS, the SVM was chosen as the default classifier; the EK-NN [5] classifier was used with EFS and REFS.

Setting the number of Bootstraps to 100, results obtained by all methods are summarized in Table 1, where the input feature space is also presented as the baseline for comparison. We can find that REFS is competitive as it led to better performance than other methods on both two imbalanced datasets. The significance of the specified prior knowledge and data rebalancing procedure for REFS was also evaluated by successively removing them. Results obtained on the lung tumor data are shown in Fig. 3, from which we can find that both of them are important for improving the feature selection and prediction performance.

$\underline{\mathbf{Analysis\;of\;Selected\;Feature\;Subsets: }}$ the indexes of features selected on both datasets with respect to 100 different Bootstraps are summarized in Fig. 4. For the lung tumor data, SUV$_{max}$ during the fifth week of radiotherapy, and the temporal change of three GLSZM-based features were stably selected; for the esophageal tumor data, TLG at staging, and two clinical characteristics were stably selected. It is worth noting that the SUV-based features selected by REFS have also been proven to have significant predictive power in clinical studies,

Fig. 5.

The KM survival curves. The two groups of patients are obtained by (a) clinical validated predictor, and (b) features selected by REFS.

e.g., the SUV$_{max}$ during the fifth week of radiotherapy has been clinically validated in [17] for NSCLC; while, the TLG (total lesion glycolysis) at staging has also been validated in [10] for oesophageal squamous cell carcinoma. Therefore, we might say that the feature subsets selected by REFS are in consistent with existing clinical studies; moreover, other kinds of features included in each subset can provide complementary information for these already validated predictors to improve the prediction performance. To support this analysis, on the esophageal tumor data which has been followed up in a long term up to five years, we drawn the Kaplan-Meier (KM) survival curves obtained by the EK-NN classifier using, respectively, the feature subset selected by REFS, and the clinically validated predictor (i.e., TLG at tumor staging). Obtained results are shown in Fig. 5, in which each KM survival curve demonstrates the fraction of patients in a classified group that survives over time. As can be seen, using REFS (Fig. 5(b)), patients were better separated as two groups with distinct survival rates than using only TLG (Fig. 5(a)).

4 Conclusion

In this paper, predicting the outcome of cancer therapy primarily based on FDG-PET images has been studied. A robust method based on Dempster-Shafer Theory has been proposed to select discriminant feature subsets from small-sized and imbalanced datasets containing noisy and high-overlapped inputs. The effectiveness of the proposed method has been evaluated by two real datasets. The obtained results are in consistent with published clinical studies. The future work is to validate the proposed method on more datasets with much higher dimensional features. In addition, how to improve the stability of involved prior knowledge should also be further studied.