Abstract
Magnetic resonance fingerprinting (MRF) quantifies various properties simultaneously by matching measurements to a dictionary of precomputed signals. We propose to extend the MRF framework by using a database to introduce additional parameters and spatial characteristics to the dictionary. We show that, with an adequate matching technique which includes an update of selected fingerprints in parameter space, it is possible to reconstruct parametric maps, synthesize modalities, and label tissue types at the same time directly from an MRF acquisition. We compare (1) relaxation maps from a spatiotemporal dictionary against a temporal MRF dictionary, (2) synthetic diffusion metrics versus those obtained with a standard diffusion acquisition, and (3) anatomical labels generated from MRF signals to an established segmentation method, demonstrating the potential of using MRF for multiparametric brain mapping.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Magnetic resonance fingerprinting (MRF) is an emerging technique for the simultaneous quantification of multiple tissue properties [7]. It offers absolute measurements of the T1 and T2 relaxation parameters (opposed to traditional weighted imaging) with an accelerated acquisition, leading to efficient parameter mapping. MRF is based on matching measurements to a dictionary of precomputed signals that have been generated for different parameters. Generally, the number of atoms in the dictionary is dictated by the amount of parameters, and the range and density of their sampling. As an alternative to continuous sampling of the parameter space, one could use measured training examples to learn the dictionary, reducing the number of atoms to only feasible parameter combinations [2]. In this work, we propose to use a database of multi-parametric datasets to create the dictionary, presenting two new features of MRF that can be achieved simultaneously with relaxation mapping: modality synthesis and automatic labeling of the corresponding tissue.
In this extended application of MRF towards image synthesis and segmentation, we follow a direction that has recently gained attention in the medical image processing literature [1, 3, 5, 6, 9, 10]. The working principle behind these methods is similar: given a source image and a multi-contrast database of training subjects, it is possible to generate the missing contrast (or label) of the source by finding similarities within the database and transferring them to create a new image. The search and synthesis strategy can take several forms: it could be iterative to incorporate more information [10]; can be optimized for multiple scales and features [1]; may include a linear combination of multiple image patches [9]; or be configured to learn a nonlinear transform from the target to the source [5]. There have been several applications of synthetic contrasts, including inter-modality image registration, super-resolution, and abnormality detection [3, 5, 6, 9, 10]. Furthermore, in addition to the creation of scalar maps in image synthesis, similar techniques can be used for mapping discrete annotations; for example, in the segmentation of brain structures [1].
Inspired by these ideas, we present a method for synthesizing modalities and generating labels from magnetic resonance fingerprints. It relies on the creation of a spatiotemporal dictionary [2] and its mapping to different parameters. Specifically, in addition to the physics-based mapping of MRF signals to the T1 and T2 relaxation parameters, we train empirical functions for a mapping of the signals to diffusion metrics and tissue probabilities. We show that we can achieve higher efficiency relaxation mapping, and demonstrate how the use of a spatiotemporal context improves the accuracy of synthetic mapping and labeling.
We see three main contributions to our work. (1) We present a framework for creating a spatiotemporal MRF dictionary from a multi-parametric database (Sect. 2.1). (2) We generalize fingerprint matching and incorporate a data-driven update to account for correlations in parameter space, allowing for the simultaneous estimation of M different parameters from any fingerprinting sequence (Sect. 2.2). (3) Depending on the nature of the m-th parameter, we call it a mapping, synthesis, or labeling, and show results for all three applications (Sect. 3.1). This is the first attempt - to the best of our knowledge - to simultaneously map parameters, synthesize diffusion metrics, and estimate anatomical labels from MR fingerprints.
2 Methods
Let \( \mathcal {Q} = \{ Q_s\}^S_{s=1}\) represent a database of spatially aligned parametric maps for S subjects, where each subject \(Q_s \in \mathbb {R}^{N \times M}\) contains a total of \(N = N_i \times N_j \times N_k \) voxels and M maps. Every map represents an individual property, and can originate from a different acquisition or modality, or even be categorical. Our database includes the quantitative relaxation parameters T1 and T2; a non-diffusion weighted image (S0); the diffusion metrics mean diffusivity (MD), radial diffusivity (RD), and fractional anisotropy (FA); and probability maps for three tissue classes: gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). Thus, for every subject \(Q_s = \{\text {T1},\text {T2},\text {S0},\text {MD},\text {RD},\text {FA},\text {GM},\text {WM},\text {CSF}\}\). We use this database to create a spatiotemporal MRF dictionary as follows.
2.1 Building a Spatiotemporal MRF Dictionary
With the relaxation parameters T1 and T2 and knowledge of the sequence variables, it is possible to follow the extended phase graph (EPG) formalism to simulate the signal evolution of a fast imaging with steady state precession MRF (FISP-MRF) pulse sequence [4]. In EPG the effects of a sequence on a spin system are represented by operators related to radio-frequency pulses, relaxation, and dephasing due to gradient moments. Therefore, for every voxel in all subjects, application of the EPG operators leads to a dictionary \(D \in \mathbb {C}^{NS \times T}\) with a total of T temporal points (see Fig. 1).
We further process the dictionary to incorporate spatial information by expanding each voxel with its 3D spatial neighborhood of dimension \(P = P_i \times P_j \times P_k\) and compressing the temporal dimension into its first V singular vectors [8]. This results in a compressed spatiotemporal dictionary \(\tilde{D} \in \mathbb {C}^{NS \times PV}\). Finally, we define a search window \(W_n = W_i \times W_j \times W_k \) around every voxel n, limiting the dictionary per voxel to \(\tilde{D}_{n} \in \mathbb {C}^{W_nS \times PV}\). The choice for a local search window has a two-fold motivation: it reduces the number of computations by decreasing the search space and it increases spatial coherence for dictionary matching [10].
Applying subject concatenation, patch extraction, and search window reduction on the database \(\mathcal {Q}\) leads to a voxel-wise spatio-parametric matrix \(\tilde{R}_n \in \mathbb {R}^{W_nS \times PM}\). For simplicity, we will use D and R instead of \(\tilde{D}_{n}\) and \(\tilde{R}_n\), where every dictionary entry \(d_c \in \mathbb {C}^{PV}\) has its corresponding matrix entry \(r_c \in \mathbb {R}^{PM}\).
2.2 Dictionary Matching and Parameter Estimation
MRF aims to simultaneously estimate several parametric maps from undersampled data. This is achieved by reconstructing an image series and matching it to the dictionary. We reconstruct V singular images [8] and extract 3D patches from them to create the patch-based matrix \({X} \in \mathbb {C}^{N \times PV}\). At every voxel \(x_n\), we find the set \(\mathcal {M}_n\) of the C highest correlated dictionary entries \(d_c,\ c=1,..,C\), by:
with the threshold value \(\tau _C\) such that \(|\mathcal {M}| = C\) and
Making use of the selected entries \(d_c\) and the corresponding parametric vectors \(r_c\), an estimated value \(\tilde{q}_{{n,m}}\) at voxel location n in map m is determined by the weighted average of the correlation between every entry \(d_c\) and the signals \(x_p\) within \(\varOmega _n\), the spatial neighborhood of n:
where \(r_{c,pm}\) indexes the quantitative value of voxel p centered around atom c in map m. Repeating this procedure for every voxel creates an estimate \(\tilde{Q}\) of all of the parametric maps, including synthetic modalities and anatomical labels.
Data-Driven Updates. Ye et al. [10] proposed the use of intermediate results to increase spatial consistency of the synthetic maps. We take a similar approach, and define a similarity function relating image space and parameter space:
where \(\alpha \) controls the contributions of the correlations in image and parameter space. The selected atoms are now determined by
In the first iteration \(\alpha = 0\) as we have no information on the map \(\hat{Q}\) for our subject. In a second iteration we increase \(\alpha \), adding weight to the similarities in parameter space and compute Eq. 5 again to find a new set of dictionary atoms. The final version of the maps is given by a modified version of Eq. 3:
This procedure is essentially a 3D patch-match over a V-dimensional image space and M-dimensional parameter space, where the matching patches are combined by their weighted correlation to create a final result.
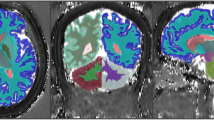
Exemplary results of one test subject with \(P = 3\times 3 \times 3\). The upper row displays the first five singular images; while the second and fourth row show the output for different parametric maps and the correlation to the reference image, displayed in the third and fifth row, respectively. Additionally, the last column in rows four and five shows labels obtained from selecting the tissue class with highest probability and the dice similarity coefficient (DSC) from the output labels to the reference. The bar underneath represents, from left to right, background, GM, WM, and CSF; and the DSC was computed from the GM, WM, and CSF labels. T1 and T2 scale is displayed in ms; S0 is qualitatively scaled to 255 arbitrary units; MD and RD are in \({\text {mm}^2}/{\text {s}}\); FA, GM, WM, and CSF are fractional values between zero and one.
2.3 Data Acquisition and Pre-processing
We acquired data from six volunteers with a FISP-MRF pulse sequence [4] on a 3T GE HDx MRI system (GE Medical Systems, Milwaukee, WI) using an eight channel receive only head RF coil. After an initial inversion, a train of \(T= 1024\) radio-frequency pulses with varying flip angles and repetition times following a Perlin noise pattern [4] was applied (see Fig. 1). We use one interleave of a zero-moment compensated variable density spiral trajectory per repetition, requiring 32 interleaves to sample a \(22 \times 22\) cm field of view (FOV) with 1.7 mm isotropic resolution. We acquired 10 slices per subject with a scan time of 13.47 seconds per slice, performed a gridding reconstruction onto a \(128 \times 128\) Cartesian grid, projected the data into SVD space, and truncated it to generate \(V = 10\) singular images. The choice of \(V = 10\) was motivated by the energy ratio, as this was the lowest rank approximation which still yielded an energy ratio of 1.0 [8]. The singular images were matched to a MRF dictionary comprising of T1 values ranging from 100 to 6,000 ms; and T2 values ranging from 20 ms to 3,000 ms.
In addition, we scanned each volunteer with a diffusion weighted imaging (DWI) protocol comprising of 30 directions in one shell with \(b=1000 \ {\text {s}}/{\text {mm}^2}\). The FOV, resolution, and acquired slices were the same as with MRF-FISP, resulting in a 15 min scan. We applied FSL processing to correct for spatial distortions derived from EPI readouts, skull strip, estimate the diffusion tensor and its derived metrics MD, RD, and FA; and used the non-diffusion weighted image S0 to compute probability maps of three tissue types (GM, WM, CSF) using [11]. Finally, we applied registration across all subjects to create the database.
3 Experiments and Results
For every subject, we performed a leave-one-out cross validation, wherein the dictionary was constructed from five subjects and the remaining subject was used as a test case. Following the procedure described in Sect. 2.2, we created a database of nine parametric maps (T1,T2,S0,MD,RD,FA,GM,WM,CSF) and compared the estimated metrics to the reference by their correlation.
We explored the influence of the window size \(W_n\), the number of entries C, and the \(\alpha \) on the estimated maps. We found correlations increased with diminishing returns as \(W_n\) increased, while adding more entries yielded smoother maps. Correlations were higher after a second iteration of data-driven updates with \(\alpha > 0\), irrespective of the value of \(\alpha \). Nonetheless, variations of these parameters didn’t have a significant effect on the overall results. To investigate the impact of using spatial information, we repeated the experiment for spatial patch sizes of \(P = 1\times 1 \times 1\), \(3\times 3 \times 3\), and \(5\times 5 \times 5\). For these experiments we used \(W_n = 11\times 11 \times 11\), \(C=5\), \(\alpha = 0.5\), and two iterations.
3.1 Results
The reference T1 and T2 maps were estimated from a FISP-MRF sequence with a temporal dictionary, while we used a spatiotemporal dictionary with varying spatial patches. Estimated T1 and T2 maps were consistent with the reference, with increasing spatial smoothness for larger spatial patches. This also lead to a decrease in correlation to the reference, most notably in T2 estimation (see Fig. 3a–b), which could also be attributed noisier T2 estimates. In future experiments we will rely on standard relaxation mapping for reference comparison.
The synthetic S0 and diffusion metrics MD, RD, and FA show spatial coherence, achieving correlation values over 0.90 with respect to a standard DWI acquisition (Fig. 2). Similar to [10], we found that FA maps were generally the least correlated to the reference. This is due to the fact that diffusion encoding in DWI acts as a proxy for underlying tissue anisotropy, whereas the measured fingerprints are not diffusion sensitive, failing to exactly recover directionality present in FA. In fact, the higher the directionality encoded in a given modality, the lower the correlation to the reference (\(\overline{\rho _{{\text {S0}}}}>\overline{\rho _{{\text {MD}}}}>\overline{\rho _{{\text {RD}}}}>\overline{\rho _{{\text {FA}}}}\)). Furthermore, for all cases in modality synthesis, incorporating spatial information generated increased consistency and higher correlated results (Fig. 3c–f).
Figure 2 shows the visual similarity between tissue probability maps obtained directly as an output from matching and those computed with [11] and the labels obtained by selecting the class with the highest probability. As with modality synthesis, anatomical labels improved when spatial information was taken into account (Fig. 3g–i). Particularly in CSF, incorporation of spatial information eliminated false positives, yielding better quality maps. On the other hand, thresholding of probability maps lead to an overestimation of GM labels, notably at tissue boundaries. Labeling at tissue boundaries could benefit from higher resolution scans and a multi-channel reference segmentation.
4 Discussion
This work proposes to replace a simulated temporal MRF dictionary with a spatiotemporal dictionary that can be learnt from data, increasing the efficiency of relaxation parameter mapping, and enabling the novel applications of modality synthesis and anatomical labeling. In terms of methodology, we borrow concepts such as the search window and parameter space regularization from the image segmentation and synthesis literature [1, 3, 10], but change the input to a V-dimensional image space and the output to an M-dimensional parameter space, making it applicable to MRF. Moreover, our framework is valid for any MR sequence, provided signal evolutions can be computed from the training data.
Results indicate that it is possible to use MRF to simultaneously map T1 and T2 parameters, synthesize modalities, and classify tissues with high consistency with respect to established methods. While our method allows us to circumvent post-processing for diffusion metric estimation and tissue segmentation, it is important to note that changes in synthetic diffusion maps can only be propagated from the information available in the database. Therefore, creating the dictionary from pathology and exploring advanced learning techniques capable of capturing these changes is the subject of future work.
References
Giraud, R., Ta, V.T., Papadakis, N., et al.: An optimized PatchMatch for multi-scale and multi-feature label fusion. NeuroImage 124, 770–782 (2016)
Gómez, P.A., Ulas, C., Sperl, J.I., et al.: Learning a spatiotemporal dictionary for magnetic resonance fingerprinting with compressed sensing. In: MICCAI Patch-MI Workshop, vol. 9467, pp. 112–119 (2015)
Iglesias, J.E., Konukoglu, E., Zikic, D., et al.: Is synthesizing MRI contrast useful for inter-modality analysis? MICCAI 18(9), 1199–1216 (2013)
Jiang, Y., Ma, D., Seiberlich, N., et al.: MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. MRM 74(6), 1621–1631 (2014)
Jog, A., Carass, A., Roy, S., et al.: MR image synthesis by contrast learning on neighborhood ensembles. Med. Image Anal. 24(1), 63–76 (2015)
Konukoglu, E., van der Kouwe, A., Sabuncu, M.R., Fischl, B.: Example-based restoration of high-resolution magnetic resonance image acquisitions. In: Mori, K., Sakuma, I., Sato, Y., Barillot, C., Navab, N. (eds.) MICCAI 2013, Part I. LNCS, vol. 8149, pp. 131–138. Springer, Heidelberg (2013)
Ma, D., Gulani, V., Seiberlich, N., et al.: Magnetic resonance fingerprinting. Nature 495, 187–192 (2013)
McGivney, D., Pierre, E., Ma, D., et al.: SVD compression for magnetic resonance fingerprinting in the time domain. IEEE TMI 0062, 1–13 (2014)
Roy, S., Carass, A., Prince, J.L.: Magnetic resonance image example based contrast synthesis. IEEE TMI 32(12), 2348–2363 (2013)
Ye, D.H., Zikic, D., Glocker, B., et al.: Modality propagation: coherent synthesis of subject-specifc scans with data-driven regularization. MICCAI 8149, 606–613 (2013)
Zhang, Y., Brady, M., Smith, S.: Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE TMI 20, 45–57 (2001)
Acknowledgments
With the support of the Technische Universität München Institute for Advanced Study, funded by the German Excellence Initiative and the European Commission under Grant Agreement Number 605162.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Gómez, P.A. et al. (2016). Simultaneous Parameter Mapping, Modality Synthesis, and Anatomical Labeling of the Brain with MR Fingerprinting. In: Ourselin, S., Joskowicz, L., Sabuncu, M.R., Unal, G., Wells, W. (eds) Medical Image Computing and Computer-Assisted Intervention - MICCAI 2016. MICCAI 2016. Lecture Notes in Computer Science(), vol 9902. Springer, Cham. https://doi.org/10.1007/978-3-319-46726-9_67
Download citation
DOI: https://doi.org/10.1007/978-3-319-46726-9_67
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46725-2
Online ISBN: 978-3-319-46726-9
eBook Packages: Computer ScienceComputer Science (R0)