Abstract
Software defined network (SDN) is an emerging network architecture that has drawn the attention of academics and industry in recent years. Affected by investment protection, risk control and other factors, the full deployment of SDN will not be finished in the short term, thus it results into a coexistence state of traditional IP network and SDN which is named hybrid SDN. In this paper, we formulate the SDN controller’s optimization problem for load balancing as a mathematical model. Then we propose a routing algorithm Dijkstra-Repeat in SDN nodes which can offer disjoint multipath routing. To make it computationally feasible for large scale networks, we develop a new Fast Fully Polynomial Time Approximation Schemes (FPTAS) based Lazy Routing Update (LRU).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Load balancing is a key technique for improving the performance and scalability of the Internet. It aims to distribute traffic so as to optimize some performance criteria. Load balancing using OSPF may cause network congestion as they are non-traffic-aware. The chief problem is that very often many comparable traffic flows are misled to converge on bottleneck links since these algorithms are oblivious to traffic characteristics and link loading.
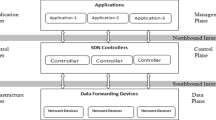
SDN is an emerging innovator to the traditional networking paradigm, which unleashes a powerful new paradigm offering flow-level traffic control and programmable interfaces to network operators. However, fully deploying the SDN in the network is by no means an easy job. We may encounter economical, organizational and technical challenges [1]. As a result, a full deployment of SDN, i.e., all the router nodes support SDN and can be centrally controlled by the controllers, in the network will not work out in the short term. Thus a hybrid SDN deployment, i.e., SDN/OSPF hybrid network is a better choice. We adopt the hybrid architecture as the research background in this work. In a hybrid SDN, only the SDN nodes can be controlled by the centralized controller, while the legacy nodes still use the traditional shortest path routing protocol OSPF to forward packets.
[2] is the first paper to address network performance issues in an incrementally deployed SDN network. It formulates the load balancing as a linear programming problem and refines a FPTAS algorithm to solve it. But [2] only uses a single shortest path to optimize the traffic passing through SDN nodes and the SDN controller must recompute the routing after forwarding one flow. The network performance is thus limited. We propose disjoint multipath calculation in SDN nodes. For the flows directed to the same destination, the SDN controller can map them to disjoint paths which could ensure that the flows do not aggregate until they reach the destination node. We also formulate the SDN controller’s optimization problem for load balancing and develop a Lazy Routing Update (LRU) scheme for solving these problems, which belongs to Fast Fully Polynomial Time Approximation Schemes (FPTAS). LRU can decrease the routing calculation in the SDN controller. It does this by spreading traffic load across all feasible links in the network. In simpler terms it means placing traffic where the capacity exists.
2 Problem Formulation
2.1 Hybrid Network Scenario
In the SDN/OSPF hybrid network, a centralized SDN controller computes the forwarding table for a set of SDN nodes. The first packet of every flow passing through SDN nodes is sent to the SDN controller, and the following operations are done by the SDN controller. The rest of the nodes in the network run traditional network protocol OSPF and forward packets along the shortest paths. In addition to forwarding packets, the SDN nodes forward some traffic measurement information to the SDN controller. The controller uses these information along with information disseminated in the network by OSPF-TE to dynamically map the routing tables to the SDN nodes in order to change traffic conditions. Note that in OSPF-TE, the nodes also exchange available bandwidth information on the links in the network. Therefore the controller knows the current OSPF costs as well as the amount of traffic flow on each link (averaged over some time period).
Figure 1 shows an example of hybrid network topology from [2]. Nodes 2, 9, 14 are SDN nodes and the rest nodes are legacy nodes. SDN nodes 2, 9, 14 are controlled externally. We will use this network to illustrate some of the concepts that we outline in the rest of the paper. We assume that all the links in the network are bidirectional and all links have the same OSPF cost. Each flow enters the network at its ingress node and has to visit a set of nodes before egressing the network at its egress node. The traffic that goes from source to destination without transiting through a SDN node will be referred to as uncontrollable traffic. If the source of a packet is a SDN node, or if it passes through at least one SDN node before it reaches its destination then the traffic will be called controllable traffic. In other words, controllable traffic comprises of packets that pass through at least one SDN node if the packets are routed using standard OSPF. There is at least an opportunity at the SDN nodes to manipulate the path of controllable traffic (Fig. 2).
2.2 Optimization Problem Definition
Given a directed graph \( G = (N,E) \), where the \( N \) and \( E \) are set of \( n \) nodes and set of \( m \) edges, respectively, with each edge capacity retrievable from a function \( c(e) \). The background traffic \( b(e) \) on each link \( e \) is readily retrieved or estimated by the controller through the dynamic information disseminated by OSPF-TE [6]. \( g(e) \) is the edge residual capacity and \( g(e) = c(e) - b(e) \). There are \( h \) flows defined as a set of ingress-egress pairs, \( K = \{ (s_{i,} t_{i} ):s_{i} ,t_{i} \in N,i = 1, \ldots ,h\} \) and associated to them are demands, \( D = \{ d(k):k \in K\} \). Note that we use edge to represent network link. Let \( P_{k} \) be the set of paths between \( s_{k} \) to \( t_{k} \) in \( G \), and let \( P = { \cup }_{{}} P_{k} \). Let \( f(p) \) denotes the amount of flow along path \( p \).
The primal linear program (LP) formulation is
\( \hbox{max} \, \varphi \)
(1) denotes that the sum of flows on all paths in \( P_{k} \) is greater than the demand of ingress-egress pairs. (2) enforces the edge capacity constraints which ensure that the total flow on the edge is less than the difference between the edge capacity \( c(e) \) and the background traffic \( b(e) \). (3) ensures non-negative flow on each candidate path. The goal is to maximize the throughput \( {\varphi } \) while not violating capacity constraints. If the optimal \( {\varphi > 1} \) then the current flow can be routed at the SDN nodes while ensuring that all edge utilizations are less than one.
We now associate dual variables \( l(e) \) with each edge capacity constraint (5) and \( z(k) \) for the demand constraint (4). It is interesting to note that its dual LP problem of the above can be shown to be
\( \hbox{min} \, \sum\nolimits_{e \in E} {l(e)g(e)} \)
Note that this problem is a constrained version of the maximum concurrent flow problem, we can adapt the Fully Polynomial Time Approximation Scheme (FPTAS) developed for a generic maximum concurrent flow problem [3] to this case at SDN controller.
3 Load Balancing in Hybrid SDN Network
3.1 Disjoint Multipath Calculation
The proposed disjoint multipath scheme determines paths as follows. First, a path between nodes i and j is found as the shortest path by Dijkstra algorithm. The Dijkstra algorithm is then repeated after excluding network links used in the first shortest path to calculate the second shortest path. After that, Dijkstra algorithm is further repeated after excluding those network links used in the first or second shortest path. This process is repeated until no more paths are obtained. The algorithm of disjoint multipath calculation is named Dijkstra-Repeat in the following of this paper. Obviously, the Dijkstra-Repeat algorithm for computing the routing table for the SDN nodes could ensure that routing will be along loop-free shortest paths while minimizing the congestion in the network.
Forwarding is a method which maps incoming packets to outgoing links. The SDN nodes act basically as forwarding elements. If there are multiple next hops for a given destination, then the SDN nodes can split traffic to the destination in a pre-specified manner across the multiple next hops, subject to load balancing.
3.2 LRU: A New FPTAS Algorithm
We assume that the traffic matrix and the topology of the network are steady for a short period. The locations and number of the SDN nodes can be fixed and determined based on greedy algorithms [2]. The \( \updelta \) is defined as the same value in [2], which is a function of the desired accuracy level \( \upomega \), the number of nodes \( n \) and the number of edges \( m \). The algorithm then operates iteratively. At the beginning of each cycle, the controller schedules controllable traffic with awareness of background traffic \( b(e) \) on each link by OSPF-TE, so as to optimize the overall load balancing. The dual weight of each edge \( e \in E \) is initialized to \( l(e) =\updelta/g(e) \), where \( g(e) \) is the remaining capacity of each edge. In each iteration, it first computes the multiple admissible paths \( P_{ut} \) between SDN nodes u and other nodes t with Dijkstra-Repeat. For the primal problem, the algorithm forwards flow along the path \( p \), while \( p \) is selected from \( P_{ut} \) with hashing. The amount of flow \( f(u) \) sent along the path \( p \) is determined by the minimum remaining link capacity \( g(e) \) on \( p \) and the controllable traffic demand \( d(u) \) between the two terminals of the path. As a result, the primal variable \( R_{ut} \) and the primal flow demand \( d(u) \) is updated by \( f(u) \), respectively. After updating the primal variables, the algorithm continues to update the dual variables \( l(e) \) related to path \( p \). The algorithm stops when \( D_{L} \ge 1 \).

The algorithm follows in the similar vein as [3]. The correctness of the algorithm as well as the running time analysis is identical to the results in the paper and is therefore omitted. Actually, the computational complexity of the FPTAS algorithm is at most a polynomial function of the network size and 1/\( \upomega \) [3]. Thus, the computational complexity of our approximation algorithm is also polynomial. There are however some key differences in the implementation of the algorithm. One key difference is that we use disjoint multipath while [3] uses a single shortest path. In fact, multipath routing can significantly reduce congestion in hot spots by distributing traffic to unused network resources instead of routing all the traffic on a single path. That is, multipath routing offers better load balancing and makes full utilization of network resources [4].
The other key difference is that our FPTAS algorithm is based on Lazy Routing Update. In each iteration, [3] has to compute the lightest admissible path from all SDN nodes to a given destination using path finding algorithm with the dual weights \( l(e) \) (not OSPF costs). The most time consuming step in practical cases is the shortest path computation. In [3], the SDN controller recomputes the shortest path after routing one flow, resulting in frequent updates on routers, which is a so time consuming process in each iteration of FPTAS algorithm that it doesn’t fit in such an online routing algorithm. So in our scenario, at the beginning of each cycle, the controller calculates admissible paths set using Dijkstra-Repeat algorithm with the traffic information from OSPF-TE. And in a short period, the SDN controller maps the flows aggregated at SDN nodes to multiple admissible paths with hashing. This process of augmenting flow is repeated until the problem is dual feasible. We call that Lazy Routing Update (LRU), as shown in Algorithm for Load Balancing.
4 Experiments and Evaluation
In this section, we conduct the simulation experiments. We ran two groups of experiments to check the effectiveness of the algorithm using the following two topologies: (i) The Geant (Europe) topology from [5]. This topology has 22 nodes and 36 links; (ii) The Abilene topology from [5]. This topology has 12 nodes and 30 links. For Geant and Abilene topology, the link weights and the link capacities are given, and we can also get the traffic matrices of the two topologies from [5]. The number of SDN nodes for the two topologies are determined as 6 and 3, respectively. The location of the SDN nodes are decided by the incremental greedy approach stated in [2].
For Geant and Abilene topology, we carry out twenty experiments with twenty traffic matrices from [5] on each topology to compare with the maximum link utilization in OSPF, HSTE [2] and our LRU. We carry out the two groups of experiments to illustrate the practicality of our algorithm, as the two topologies used in the experiments are real and the traffic is actually measured. The results are shown in Figs. 3 and 4. As the figures illustrate, our algorithm LRU in the figures obtains a lower maximum link utilization compared with the other two algorithms. Compared with HSTE, LRU can reduce the overall maximum link utilization by 10 % and 9 % for Geant and Abilene topologies, respectively. Compared with OSPF, the reductions are 20 % and 17 %.
5 Conclusion
The SDN/OSPF hybrid network load balancing is a popular problem that raises people’s attention worldwide. It deviates from the traditional load balancing scenario, where the flows are always routed along the shortest paths. The emerging of SDN provides a new method to solve the load balancing problem. It can centrally control the flows that directed to the outgoing links of the SDN nodes, which is similar with the model of multi-commodity. In this paper, we propose a new FPTAS algorithm LRU to solve the load balancing problems in SDN/OSPF hybrid network. Compared with other load balancing algorithms, the proposed algorithm reduces the SDN calculation and obtains a lower maximum link utilization. In the future work, we will carry out the experiments on the testbed and consider more hybrid SDN network types.
References
Vissicchio, S., Vanbever, L., Bonaventure, O.: Opportunities and research challenges of hybrid software defined networks. ACM SIGCOMM Comput. Commun. Rev. 44(2), 70–75 (2014)
Agarwal, S., Kodialam, M., Lakshman, T.: Traffic engineering in software defined networks. In: Proceedings of the IEEE INFOCOM, pp. 2211–2219 (2013)
Garg, N., Konemann, J.: Faster and simpler algorithms for multicommodity flow and other fractional packing problems. SIAM J. Comput. 37(2), 630–652 (2007)
Dasgupta, M., Biswas, G.: Design of multi-path data routing algorithm based on network reliability. Comput. Electr. Eng. 38(6), 1433–1443 (2012)
SDNlib. http://sndlib.zib.de/home.action
Nascimento, M.R., Rothenberg, C.E., Salvador, M.R., Corrêa, C.N., de Lucena, S.C., Magalhaes, M.F.: Virtual routers as a service: the routeflow approach leveraging software-defined networks. In: Proceedings of the 6th International Conference on Future Internet Technologies, pp. 34–37. ACM (2011)
Acknowledgments
This research is sponsored by the State Key Program of National Natural Science Foundation of China No. 61533011, Shandong Provincial Natural Science Foundation under Grant No. ZR2015FM001, the Fundamental Research Funds of Shandong University No. 2015JC030.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Sun, X., Jia, Z., Zhao, M., Zhang, Z. (2016). Multipath Load Balancing in SDN/OSPF Hybrid Network. In: Gao, G., Qian, D., Gao, X., Chapman, B., Chen, W. (eds) Network and Parallel Computing. NPC 2016. Lecture Notes in Computer Science(), vol 9966. Springer, Cham. https://doi.org/10.1007/978-3-319-47099-3_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-47099-3_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47098-6
Online ISBN: 978-3-319-47099-3
eBook Packages: Computer ScienceComputer Science (R0)