Abstract
The problem of fault model-based test generation from formal models, in this case Finite State Machines, is addressed. We consider a general fault model which is a tuple of a specification, conformance relation and fault domain. The specification is a deterministic FSM which can be partially specified and not reduced. The conformance relation is quasi-equivalence, as all implementations in the fault domain are assumed to be completely specified FSMs. The fault domain is a set of all possible deterministic submachines of a given nondeterministic FSM, called a mutation machine. The mutation machine contains a specification machine and extends it with mutated transitions modelling potential faults. An approach for deriving a test suite which is complete (sound and exhaustive) for the given fault model is elaborated. It is based on our previously proposed method for analyzing the test completeness by logical encoding and SMT-solving. The preliminary experiments performed on an industrial controller indicate that the approach scales sufficiently well.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- FSM
- Conformance testing
- Mutation testing
- Fault modelling
- Fault model-based test generation
- Test coverage
- Fault coverage analysis
1 Introduction
Fault model-based testing receives constantly growing interests of both researchers and test practitioners. Fault models are defined in the literature in a variety of ways [16]. The work [10] proposes to define a fault model as a tuple of a specification, conformance relation and fault domain. In the context of testing from finite state machines, the specification is a certain type of FSM. A conformance relation is specific to the FSM type and for completely specified deterministic machines it is equivalence, while for partially specified machines it is quasi-equivalence. The fault domain is a set of implementation machines, aka mutants, each of which models some faults, such as output, transfer and transition faults.
In the traditional checking experiment theory the fault domain is the universe of all machines with a given number of states and input and output alphabets of the specification, see, e.g., [7, 8, 11–13]. Checking experiments are in fact sound and exhaustive, i.e., complete tests. However, their size for realistic specifications is often considered too big for practical applications. To us, this is a price to pay for considering the universe of all FSMs. Intuitively, choosing a reasonable subset of this fault domain might be the way to mitigate the test explosion effect. As an example, if one considers the fault domain of mutants that model output faults, a test complete for this fault model is simply a transition tour. The fault domains intermediate to these two domains have not yet received in our opinion sufficient attention.
To define a fault domain which is a subset of the universe of all FSMs, one could explicitly enumerate mutants as in program or model-based mutation testing, see, e.g., [1–3, 21] or avoid this enumeration by defining a fault domain as a set of all possible submachines of a given nondeterministic FSM, called a mutation machine [4, 6, 9]. The mutation machine contains as a submachine a specification machine, additional transitions model potential faults. Several methods were developed for test generation using this fault model [4, 6, 9, 22]. All these methods are adaptations of classical checking experiments for a fault domain defined by a mutation machine. A checking experiment is in fact a complete test suite, however, the use of the state identification approach imposes limitations on the fault model. First, the specification machine must be completely specified and reduced, so that state identifiers exist. Second, the mutation machine was defined only for such specification machines. The existing methods are not applicable for partial specification machines and mutation machines derived from them. Finally, the state identification approach does not support iterative test generation with a mutation machine allowing the tester to terminate the process when a complete test suite for the given fault model is not yet obtained, but facing the scalability problems he is forced to make a compromise between fault coverage and test length.
Addressing the above limitations, in our recent work [20], we have developed a method for analyzing the test completeness for a fault model using a mutation machine. The analysis approach is based on logical encoding and SMT-solving, it avoids enumeration of mutants while still offering a possibility to estimate the test adequacy (mutation score). This method paves a road to a test generation approach which uses the results of the analysis to find tests which kill mutants survived a current test suite and iterates until a test suite complete for a given fault model with a mutation machine is obtained or the tester decides to terminate it earlier. Elaboration of the iterative test generation approach which is based on the test completeness analysis and does not require the specification machine to be complete and reduced is the main goal of this paper.
The remaining of this paper is organized as follows. Section 2 defines a specification model as well as a fault model. In Sect. 3, we develop an approach for complete test suite generation for a given fault model with a mutation machine. Section 4 reports some results of experimental evaluation of the approach. Section 5 summarizes our contributions and indicates future work.
2 Background
2.1 Finite State Machines
A Finite State Machine (FSM) M is a 5-tuple (S, s 0, I, O, T), where S is a finite set of states with initial state s 0; I and O are finite non-empty disjoint sets of inputs and outputs, respectively; T is a transition relation T ⊆ S × I × O × S, (s, i, o, s′) is a transition.
M is completely specified (complete FSM) if for each tuple (s, x) ∈ S × I there exists transition (s, x, o, s′) ∈ T; M is partially specified (partial FSM), if for some (s, x) ∈ S × I there is no transition, we say in this case that input x is not specified in state s. Let P M denote the set of all pairs (s, x) for which M has no transitions.
M is deterministic (DFSM) if for each (s, x) ∈ S × I there exists at most one transition (s, x, o, s′) ∈ T; if there are several transitions for some (s, x) ∈ S × I then it is nondeterministic (NFSM).
An execution of M from state s is a sequence of transitions forming a path from s in the state transition diagram of M. The machine M is initially connected, if for any state s ∈ S there exists an execution from s 0 to s. Henceforth, we assume that all FSMs are initially connected. An execution is deterministic if each transition (s, x, o, s′) in it is the only transition for (s, x) ∈ S × I; otherwise, i.e., if for some transition (s, x, o, s′) in the execution there exists in it a transition (s, x, o′, s′′) such that o ≠ o′ or s′ ≠ s′′, the execution is nondeterministic. Clearly, a DFSM has only deterministic executions, while an NFSM can have both.
A trace of M in state s is a string of input-output pairs which label an execution from s. Let Tr M (s) denote the set of all traces of M in state s and Tr M denote the set of traces of M in the initial state. Given sequence β ∈ (IO)*, the input (output) projection of β, denoted β↓I (β↓O ), is a sequence obtained from β by erasing symbols in O (I). Given a trace β in state s the input projection β↓I is an input sequence defined in state s. We use Ω M (s) to denote the set of all the input sequences defined in state s and Ω M to denote the set of all the input sequences defined in state s 0. Clearly, if M is complete then Ω M = I*.
We say that an input sequence triggers an execution of M (in state s) if it is the input projection of a trace of the execution of M (in state s).
Given input sequence α ∈ Ω M , let out M (s, α) denote the set of all output sequences which can be produced by M in response to α at state s, that is out M (s, α) = {β↓O | β ∈ Tr M (s) and β↓I = α}.
We define several relations between states in terms of traces. Given states s 1, s 2 of an FSM M = (S, s 0, I, O, T), s 1 and s 2 are (trace-) equivalent, s 1 ≃ s 2, if Tr M (s 1) = Tr M (s 2); s 2 is trace-included into (is a reduction of) s 1, s 2 ≤ s 1, if Tr M (s 2) ⊆ Tr M (s 1). M is reduced if any pair of its states are distinguishable, i.e., for every s 1, s 2 ∈ S there exists α ∈ Ω M (s 1) ∩ Ω M (s 2) such that out M (s 1, α) ≠ out M (s 2, α), α is called a distinguishing sequence for states s 1 and s 2, this is denoted s 1 ≄α s 2 or simply s 1 ≄ s 2.
We also use relations between machines. Given FSMs M = (S, s 0, I, O, T) and N = (P, p 0, I, O, N), M ≤ N if s 0 ≤ p 0; N ≃ M if s 0 ≃ p 0; N ≄ M if s 0 ≄ p 0.
In this paper, we assume that a specification machine is a DFSM which could be complete or partial, but all the implementation machines are complete DFSMs. This implies that we should use the quasi-equivalence relation [17] as a conformance relation between implementation and specification machines. Given a DFSM M = (S, s 0, I, O, T) and DFSM N = (P, p 0, I, O, N), N is quasi-equivalent to M if M is a reduction of N.
Given a complete FSM M = (S, s 0, I, O, T), a machine N = (S′, s 0, I, O, N) is a submachine of M if S′ ⊆ S and N ⊆ T. The set of all complete deterministic submachines of M is denoted Sub(M). Obviously, each machine in Sub(M) is a reduction of M; moreover, if M is deterministic then Sub(M) contains just M.
2.2 Fault Model
We define the so-called mutation machine for a given specification machine by generalizing the definition previously given only a complete specification FSM [4, 6, 9, 20, 22] to allow the latter to be partially specified.
Definition 1.
Let A = (S, s 0 , I, O, N) be a specification DFSM with the set of state-input pairs P A for which A has no transitions. A complete NFSM M = (S, s 0 , I, O, T) is a mutation machine of A, if {(s, x, o, s′) | (s, x) ∈ P A , o ∈ O, s′ ∈ S} ⊆ T and A is a submachine of M.
In this definition we interpret inputs which are not specified in some states of A as don’t care inputs. This implies that in a conforming implementation these inputs may cause transitions with an arbitrary output to any state in S.
The transitions T of the mutation machine can be classified as follows. The transitions in the set {(s, x, o, s′) | (s, x, o, s′) ∈ T, (s, x) ∈ P A } are called don’t care transitions; we let DNC M denote this set. The transitions in T ∩ N are common for M and A, these are unaltered transitions. Transitions in the set T\ (N ∪ DNC M ), are mutated transitions. Given (s, x) ∈ S × I, we let T sx denote the set of transitions from state s and input x in M. If T sx is a singleton then its transition is called a trusted transition. The set T sx is called a suspicious set of transitions if it is not a singleton, transitions in a suspicious set are called suspicious. Notice that don’t care transitions are also treated as suspicious, since they can either compensate faults represented by mutated transitions and form a conforming mutant or expose wrong outputs.
We assume that all possible implementation machines for the specification machine A constitute the fault domain Sub(M), the set of all deterministic submachines of the mutation machine M of A. A submachine B ∈ Sub(M), B ≠ A is called a mutant. All mutants share all the trusted transitions, they may differ in suspicious and don’t care transitions. In fact, transitions in suspicious sets are alternative and only one can be present in a deterministic mutant. Similarly, each mutant has a single transition for each pair (s, x) ∈ P A , as all mutants are complete machines. A mutant B is conforming if it is quasi-equivalent to A, otherwise, it is nonconforming. We say that input sequence α ∈ Ω A detects or kills the mutant B if B ≄α A.
The tuple <A, ≃, Sub(M)> is a fault model [10]. For a given specification machine A quasi-equivalence relation partitions the set Sub(M) into conforming and nonconforming implementations. In this paper, we do not require the FSM A to be complete and reduced. A conforming mutant may therefore have fewer states than the specification A; on the other hand, we assume that no fault creates new states in implementations, hence mutants with more states than the specification FSM are not in the fault domain Sub(M).
Consider the example in Fig. 1.
The specification machine A in Fig. 1 is a partial DFSM, where input b is not specified in state 2, hence P A = {(2, b)}. The machine is not reduced, since state 3 is quasi-equivalent to state 2. All the existing methods for test generation using mutation machines [4, 6, 9, 22] cannot be applied for such a machine, as they are based on the assumption that the specification machine is a complete and reduced machine, as required by the state identification approach.
The mutation machine M in Fig. 1 has three mutated transitions, one representing an output fault and the other two transfer faults. It also has 14 suspicious transitions, eight of them are don’t care transitions.
The mutation machine M represents mutants as its deterministic submachines. Their number is given by the following formula:
In our running example, the number of mutants is 8 × 2 × 2 × 2 = 64.
In the extreme case, considered in classical checking experiments a fault domain is the universe of all machines with at most n states, the number of states in the specification machine, and the alphabets of it. The corresponding mutation machine becomes in this case a chaos machine with all possible transitions between each pair of states. We use Chaos(A, n) to denote such a mutation machine for A. The number of FSMs it represents is the product of the numbers of states and outputs to the power of the product of the numbers of states and inputs.
3 Mutation Testing
A finite set of finite input sequences E ⊂ Ω A is a test suite for A. A test suite is said to be complete w.r.t. the fault model <A, ≃, Sub(M)> if for each nonconforming mutant B ∈ Sub(M) it contains a test detecting B.
In the case where M = Chaos(A, n) a complete test suite is called n-complete. This notion coincides with the classical notion of checking experiments for the fault domain consisting of FSMs with at most n states [5, 7, 10].
In the domain of program mutation testing, such a test suite is often called adequate for a program relative to a finite collection of programs (in our case the set Sub(M)), see, e.g., [3].
For deterministic FSMs tests that kill a given mutant FSM can be obtained from the product of the two machines, see, e.g., [1, 2, 17]. This approach can also be used to check whether a given test kills mutants, but it requires mutant enumeration.
In this work, we develop an approach for complete test suite generation for the fault model <A, ≃, Sub(M)>, where A can be a partial or complete FSM not necessary reduced. It is based on mutant killing, but does not check mutants one by one, thus avoiding their full enumeration.
3.1 Distinguishing Automaton
Tests detecting mutants of the specification can be determined using a product of the specification and mutation machines obtained by composing their transitions as follows.
Definition 2 [20].
Given a specification machine A = (S, s 0, I, O, N) and a mutation machine M = (S, s 0, I, O, T) of A, a finite automaton D = (C ∪ {∇}, c 0, I, D, ∇), where C ⊆ S × S, and ∇ is an accepting (sink) state is the distinguishing automaton for A and M, if it holds that
-
c 0 = (s 0, s 0)
-
For any (s, t) ∈ C and x ∈ I, ((s, t), x, (s′, t′)) ∈ D, if there exist (s, x, o, s′) ∈ N and (t, x, o′, t′) ∈ T, such that o = o′ and ((s, t), x, ∇) ∈ D, if there exist (s, x, o, s′) ∈ N and (t, x, o′, t′) ∈ T, such that o ≠ o′.
Notice that there is no outgoing transition with an input from a state of the distinguishing automata if and only if the state includes a state of A for which the input not specified.
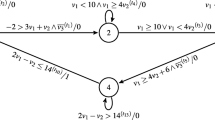
We illustrate the definition using the specification and mutation machines in Fig. 1. Figure 2 presents the distinguishing automaton for A and M.
The distinguishing automaton D for the specification A and mutation M machines in Fig. 1, state 11 is the initial state.
The accepting state defines the language L D of the distinguishing automaton D for A and M and possesses the following properties. First, L D ⊂ Ω A , then all input sequences detecting each and every mutant belong to this language.
Theorem 1.
Given the distinguishing automaton D for A and M, if B ≄α A for some B ∈ Sub(M), then there exists β ∈ L D , such that B ≄β A and β is a prefix of α.
Notice that for any nonconforming mutant there exists an input sequence of length at most n 2, where n is the number of states of the specification machine, since a distinguishing automaton has no more than n 2 states.
An input sequence α ∈ L D triggers an execution in the distinguishing automaton D which is defined by an execution in the specification machine A and some execution in the mutation machine M triggered by α. The latter to represent a mutant must be deterministic. Such a deterministic execution of the mutation machine M defining an execution of the distinguishing automaton D to the sink state is called α-revealing. An input sequence triggering revealing executions enjoys a nice property of being able to detect mutants. Moreover all its extensions also detect at least the same mutants.
Theorem 2.
[20]. Given an input sequence α ∈ Ω A such that α ∈ L D , an α-revealing execution includes at least one mutated transition, moreover, each mutant which has this execution is detected by the input sequence α.
Given an input sequence α ∈ L D , the question arises how all the mutants (un) detected by this input sequence can be characterized. We address this question in the next section.
3.2 Characterisation of Mutants (Un)Detected by an Input Sequence
Consider an input sequence α ∈ Ω A whose prefixes trigger α-revealing executions. These executions characterize mutants detected by α, since each of them defines a distinct set of suspicious transitions involved in the execution. Based on these sets we can build a constraint on transition sets of mutants undetected by α. This can be achieved by using a distinguishing automaton constrained to a given input sequence.
Let Pref(α) be the set of all prefixes of α. We define a linear automaton (Pref(α), ε, I, D α), such that each prefix of α is a state, and (β, x, βx) ∈ D α if βx ∈ Pref(α).
Definition 3 [20].
Given a specification machine A = (S, s 0, I, O, N), input sequence α ∈ Ω A , and mutation machine M = (S, s 0, I, O, T), a finite automaton D α = (C α ∪ {∇}, c 0, I, D α, ∇), where C α ⊆ Pref(α) × S × S, and ∇ is a designated sink state is the α-distinguishing automaton for A and M if it holds that
-
c 0 = (ε, s 0, p 0)
-
For any (β, s, t) ∈ C α and x ∈ I, such that βx ∈ Pref(α), ((β, s, t), x, (βx, s′, t′)) ∈ D α, if there exist (s, x, o, s′) ∈ N, (t, x, o′, t′) ∈ T, such that o = o′ and ((β, s, t), x, ∇) ∈ D, if there exist (s, x, o, s′) ∈ N, (t, x, o′, t′) ∈ T, such that o ≠ o′.
For α = bababa in our running example, the α-distinguishing automaton for A and M is shown in Fig. 3.
The α-distinguishing automaton D α for the specification A machine and mutation machine M in Fig. 1, where α = bababa.
There are eleven executions of the mutation machine listed below which are defined by five executions of the α-distinguishing automaton reaching the sink state in Fig. 3. Suspicious transitions are in bold font and the others are trusted transitions. Transitions of the specification are underlined. Three executions, namely executions 9, 10, and 11, are non-deterministic. The first eight executions belong to mutants detected by bababa.
-
1.
\( \underline{{(1,b,0,2)(2,a,0,3)}} {\mathbf{(3,}}\,\user2{b}{\mathbf{,0,3)}}\underline{{{\mathbf{(3,}}\,\user2{a}{\mathbf{,0,3)}}}} \)
-
2.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,1,2)}} \)
-
3.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,1,1)}} \)
-
4.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,1,3)}} \)
-
5.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,1,4)}} \)
-
6.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,3)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(3,}}\,\user2{b}{\mathbf{,0,3)(3,}}\,\user2{a}{\mathbf{,1,3)}} \)
-
7.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,0,3)(3,}}\,\user2{a}{\mathbf{,1,3)}} \)
-
8.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,0,4)(4,}}\,\user2{a}{\mathbf{,1,2)}} \)
-
9.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,3)}}}} {\mathbf{(3,}}\,\user2{a}{\mathbf{,1,3)}}\underline{{{\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)(4,}}\,\user2{a}{\mathbf{,1,1)}}}} \)
-
10.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,3)}}}} {\mathbf{(3,}}\,\user2{a}{\mathbf{,1,3)}}\underline{{{\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)}} \)
-
11.
\( \underline{{(1,b,0,2)(2,a,0,3){\mathbf{(3,}}\,\user2{b}{\mathbf{,0,4)}}}} {\mathbf{(4,}}\,\user2{a}{\mathbf{,1,2)(2,}}\,\user2{b}{\mathbf{,0,4)}}\underline{{{\mathbf{(4,}}\,\user2{a}{\mathbf{,1,1)}}}} \)
Three prefixes of bababa, namely baba, babab and bababa belong to L D and trigger α-revealing executions in the mutation machine. Any deterministic execution of the mutation machine with the input sequence baba is α-revealing if it uses the two suspicious transitions involved in the first execution, i.e., (3, b, 0, 3) and (3, a, 0, 3). We recall that trusted transitions are used in every mutant submachine. Hence, every mutant which has both these suspicious transitions is detected by baba. Considering all eight executions, any mutant which has any of the eight sets of suspicious transitions is nonconforming and detected by bababa. Conversely, any mutant undetected by bababa must have mutated transitions such that do not form any of the sets defined by the listed executions. This property can be formalized as a constraint on suspicious transitions using conditional operators {= , ≠} and logical operators {∧, ∨} for constraint formulas.
Given a pair (s, x) ∈ S × I such that T sx is a suspicious set of transitions, we introduce an auxiliary variable z sx which takes values from the indexes of the transitions of the mutation machine in T sx .
Each α-revealing execution e of the mutation machine involving the set of suspicious transitions {t 1, t 2, …, t n } yields a clause c e = ((z s1 × 1 ≠ t 1) ∨ (z s2 × 2 ≠ t 2) ∨ … ∨ (z snxn ≠ t n )) where s i and x i are the source state and the input of transition t i for 1 ≤ i ≤ n. The clause c e is satisfied whenever z sixi is not t i for some 1 ≤ i ≤ n. A solution of c e excludes at least one transition in e.
In the running example, the sets of suspicious transitions indexed with an integer identifier are:
T 2b = {(2, b, 0, 2)3, (2, b, 1, 2)4, (2, b, 0, 1)5, (2, b, 1, 1)6, (2, b, 0, 3)8, (2, b, 1, 3)9, (2, b, 0, 4)10, (2, b, 1, 4)11}, T 3a = {(3, a , 0, 3) 12, (3, a, 1, 3)13}, T 3b = {(3, b, 0, 3)14, (3, b , 0, 4) 15} and T 4a = {(4, a , 1, 1) 17, (4, a, 1, 2)18}. The remaining trusted transitions are indexed as follows: (1, a , 0, 1) 1, (1, b , 0, 2) 2, (2, a , 0, 2) 7, (4, b , 0, 2) 16. So we consider four variables z 2b , z 3a , z 3b and z 4a whose domains are T 2b , T 3a , T 3b , and T 4a , respectively. To simplify the presentation we use transition identifiers in constraints. The constraint formula for bababa consists of a preamble and eight clauses. The preamble (z 2b ∈ T 2b ) ∧ (z 3a ∈ T 3a ) ∧ (z 3b ∈ T 3b ) ∧ (z 4a ∈ T 4a ) specifies the domains of the variables, thus constraining the possible solutions of the conjunction of the eight clauses to transitions of the mutation machine.
((z 2b ∈ T 2b ) ∧ (z 3a ∈ T 3a ) ∧ (z 3b ∈ T 3b ) ∧ (z 4a ∈ T 4a ) ∧ ((z 3a ≠ 12) ∨ (z 3b ≠ 14)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 4) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 6) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 9) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 11) ∨ (z 3b ≠ 15)) ∧ ((z 3a ≠ 13) ∨ (z 3b ≠ 14)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 8) ∨ (z 3a ≠ 13) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 10) ∨ (z 3b ≠ 15))).
Clearly, the constraint always has a solution where values of variables determine all the unaltered transitions, but to find nonconforming mutants we need a solution if it exists which has at least one mutated transition. To this end, we add the constraint ((z 3a ≠ 12) ∨ (z 3b ≠ 15) ∨ (z 4a ≠ 17)) excluding the solution defining the specification machine augmented with an arbitrary don’t care transition, called a completed specification machine.
The final constraint formula for bababa is C(bababa) = ((z 2b ∈ T 2b ∧ z 3a ∈ T 3a ∧ z 3b ∈ T 3b ∧ z 4a ∈ T 4a ) ∧ ((z 3a ≠ 12) ∨ (z 3b ≠ 14)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 4) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 6) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 9) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 11) ∨ (z 3b ≠ 15)) ∧ ((z 3a ≠ 13) ∨ (z 3b ≠ 14)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 8) ∨ (z 3a ≠ 13) ∨ (z 3b ≠ 15)) ∧ ((z 4a ≠ 18) ∨ (z 2b ≠ 10) ∨ (z 3b ≠ 15)) ∧ ((z 3a ≠ 12) ∨ (z 3b ≠ 15) ∨ (z 4a ≠ 17))).
The constraint C(α) characterizing the mutants undetected by an input sequence α is the conjunction of a clause excluding all completed specification machines and the clauses generated for every α-revealing execution. Any existing constraint solver, e.g., Z3 [15], could be used for satisfiability checking. A solution of C(α) if it exists is an assignment of the auxiliary variables. The mutant defined by such a solution includes the transitions specified by the solution along with all the trusted transitions of the mutation machine. Any nonconforming mutant detected by α cannot be defined by any solution of C(α), only conforming mutants can.
Algorithm 1 presents a procedure that builds a constraint C TS for a given test suite TS out of the constraints for each test in the test suite.

Theorem 3.
Let C TS be a constraint specifying undetected mutants by the test suite TS. TS is complete w.r.t. the fault model <A, ≃, Sub(M)> if and only if C TS is unsatisfiable or every solution of C TS defines a conforming mutant.
In the running example, to solve the constraint formula C(bababa), we use the SMT solver Z3 [15] which finds the solution z 2b = 11, z 3a = 13, z 3b = 15, z 4a = 17. The solution defines a mutant with all trusted transitions, one don’t care transition (2, b, 1, 4)11 and one mutated transition (3, a, 1, 3)13. The mutant is presented in Fig. 4. The mutant is nonconforming, which can be verified with the help of a distinguishing automaton obtained for the specification machine and the mutant also shown in Fig. 4.
Notice that the solver could find another solution of the C(bababa), namely, z 2b = 11, z 3a = 12, z 3b = 15, z 4a = 17 which defines a conforming mutant.
Given an initial test suite TS init , the question arises how to augment TS init with new input sequences to detect all nonconforming mutants. We elaborate a complete test suite generation procedure in the next section.
3.3 Complete Test Suite Generation
We are given a test suite TS init ⊆ Ω A and a fault model <A, ≃, Sub(M)>. We want to add test cases to TS init to obtain a complete test suite. Constraints defined in the previous section can be used to analyse the completeness of a test suite, elaborated in our previous work [20]. If the constraint for a test suite has no solution or the first solution computed by a solver defines a nonconforming mutant, we can immediately assert the incompleteness of the test suite. If however the solution defines a conforming mutant, the search continues such that the mutant will not be found again in a new round of satisfiability checking. This process iterates until no new solution is found or the generated solution defines a nonconforming mutant. A witness nonconforming mutant can be used to determine a test case which detects the mutant. A new test can kill other nonconforming mutants. Hence the constraints generated by this test should be added to the ones of the current test suite. The search terminates when the current constraint is unsatisfiable which indicates that the test suite is complete. The test generation procedure is formalized in Algorithm 2.
The algorithm has two loops. The coverage analysis loop includes statements in lines 7 to 9 and the test generation loop includes statements at lines 4 to 13. The former loop is nested in the latter. When the current test suite is not complete, the execution of the test generation loop augments (in line 4) it with a new test case and updates the constraint of the current test suite with that of the generated test case. Then the coverage analysis loop is executed checking the completeness of the updated test suite, searching for a new nonconforming mutant. To this end, constraints excluding conforming mutants defined by the found solutions are iteratively added to the current constraint. The procedure terminates when the resulting constraint is unsatisfiable, indicating that the current test suite is complete or the solver generates a solution defining a nonconforming mutant. In this case, the execution of the test generation loop augments the current test suite with a new test killing the mutant. It is determined by finding the shortest path to the sink state of the distinguishing automaton of the mutant and the specification.

Theorem 4.
Procedure TestSuiteGen always terminates with a complete test suite.
Proof.
The procedure TestSuiteGen terminates as the test generation loop terminates. It does so because a mutation machine has a finite number of submachines and the solution defining a particular mutant is generated at most once. According to Theorem 2, the computed tests are revealing input sequences. On termination of the procedure the final constraint characterizing undetected mutants excludes all conforming mutants and it is unsatisfiable. Based on Theorem 3 we have that the test suite returned by the procedure is complete.
To generate a complete test suite for the running example we consider the initial test suite TS init = {bababa}, used in Sect. 3.2. Procedure TestSuiteGen first goes into the test generation loop which builds C new = C(bababa), updates TS and C to {bababa} and C(bababa) defined in Sect. 3.2. Then the coverage analysis loop finds the solution of C defining the nonconforming mutant in Fig. 4. The test baa is then generated by determining the only shortest path to the sink state in the distinguishing automaton for the specification and the mutant, so TS new becomes {baa}. Then the constraint C new = C(baa) = (z 3a ≠ 13) is generated in line 5, TS becomes {bababa, baa} and C = C(bababa) ∧ C(baa). The solution of C defines a nonconforming mutant killed by the test babaaba, the input sequence of the shortest path to the sink state the distinguishing automaton for the new nonconforming mutant and the specification, then TS new becomes {babaaba}. The constraint C new = C(babaaba) = (((z 3a ≠ 12) ∨ (z 3b ≠ 14)) ∧ ((z 3a ≠ 13) ∨ (z 3b ≠ 14)) ∧ ((z 4a ≠ 18) ∨ (z 3b ≠ 15))) is generated; it includes one clause for each of the three α-revealing executions triggered by babaaba. TS becomes {bababa, baa, babaaba} and C = C(bababa) ∧ C(baa) ∧ C(babaaba). C is satisfiable and the procedure iteratively generates only conforming mutants augmenting C each time with a constraint excluding the last conforming mutant. No additional tests are generated. The conjunction of C with the eight constraints excluding eight conforming mutants is unsatisfiable. The procedure returns a complete test suite TS = {bababa, baa, babaaba}. Notice that it generated only ten out of total 64 mutants.
The procedure TestSuiteGen also generates a complete test suite starting when the initial test suite contains just an empty input sequence.
In the next section we present experimental results obtained with a prototype tool.
4 Experimental Results
We have developed a prototype tool implementing the proposed method for complete test suite generation. In this section we present the tool and some experimental results using it.
4.1 Prototype Tool
The prototype tool is composed of four modules: an I/O module, a completeness checking module, a test generation module and a module for solver execution. The I/O module converts input data into an internal representation for processing and obtained results into a human-readable format. To this end, it implements an ANTLR-based parser [19] to interpret the mutation machine specified in a text format; it also parses the output of SMT solver Z3 [15] to extract a solution and builds a mutant. The completeness checking module builds α-distinguishing automata, determines revealing executions of the mutation machine and generates constraints for the solver. The test generation module iteratively calls the former module. The prototype can also be used with other SMT solvers compatible with the SMT-LIB 2.0.
For the experiments we use a desktop computer with the following settings: 3.4 Ghz Intel Core i7-3770 CPU, 16.0 GB of RAM, Z3 4.3.2, and ANTLR 4.5.1.
4.2 Test Generation for an Automotive Controller
We consider as a case study an automotive controller of the air quality system (HVAC), which we also used in our previous work [18, 20]. The functionality of the controller is to set an air source position depending on its current state and input from the environment.
The controller initially specified as a hierarchical Simulink Stateflow model is converted into an FSM with 14 states, 24 inputs and 24 × 14 = 336 transitions.
Several mutation machines were used in the experiments. The first one M hvac was obtained by adding 46 mutated transitions to the specification machine (details are available in [20]). The formula in Sect. 2 gives the number of mutants 312 × 217 = 69,657,034,752.
The other mutation machines were built by adding more mutated transitions to M hvac . In particular, 20, 100, 428, 764 and 1000 mutated transitions were randomly added, resulting in five more mutation machines, M +20, M +100, M +428, M +764 and M +1000. Table 1 presents the numbers of mutated transitions, mutants, generated tests and the computation time. Each generated mutant was non-conforming, so their number coincides with that of the tests, conforming mutants were never generated. The third column of Table 1 represents the average values for 30 mutation machines randomly generated by adding 20 mutated transitions to M hvac .
The experimental results indicate that the approach scales sufficiently well on a typical automotive controller even with the large number of mutants.
5 Conclusions
In this paper we focused on generation of a complete test suite detecting all nonconforming implementations in a fault domain defined by a mutation machine. A mutation machine is a nondeterministic FSM, interpreted as a compact representation of a set of deterministic implementations of a system represented by a partially or completely specified FSM. Each deterministic submachine of the mutation machine models an implementation.
We proposed a method for generating a complete test suite which avoids complete enumerations of nonconforming mutants. The method iteratively builds constraints specifying mutants undetected by an incomplete (possibly empty) test suite and uses a solution of constraints generated by a solver to determine an undetected mutant from which a new test case is selected and derives an augmented constraint for a next iteration step until the obtained constraint becomes unsatisfiable.
While it enumerates all conforming mutants, which exist mostly when the specification is partial or unreduced FSM, it does not generate all nonconforming ones. The experimental results with a prototype tool which uses the SMT solver Z3 indicate that the number of generated nonconforming mutants reaches only a small percentage of all mutants represented by a mutation machine.
Novelty of the contributions of this paper are as follows. The proposed approach allows one to construct checking experiments for FSMs which are not necessarily complete and reduced without using any state identification facility such as characterization sets, distinguishing sequences, and state identifiers, as opposed to traditional checking experiment approaches. Thus, we demonstrate that it is possible to construct checking experiments using logical encoding and constraint solving instead of classical methods based on state identification [4, 6, 9, 22]. Moreover, test completeness is guaranteed for a predefined subset of the universe of all FSMs with a given number of states, represented by a mutation machine. Compared to all previous work on the use of mutation machine [4, 6, 9, 20, 22], we have generalized its definition to make it applicable to partially defined specification machines. The method proposed in [22] is only applicable to mutation machines which satisfy the following assumption. If a transition of the specification machine becomes suspicious in the mutation machine then the latter has all possible (thus chaotic) suspicious transitions from the start state of the transition caused by the same input. The method also requires the specification machine be completely specified. Compared to that work, our method is applicable to arbitrary mutation machines, while the specification machine is allowed to be partially specified.
Another interesting feature of the approach is that it is iterative and allows the tester to obtain an incomplete test suite for which fault coverage can be estimated (as discussed in [20]) when facing the scalability problems he is forced to make a compromise between fault coverage and test length.
The experiments indicate that the proposed approach may scale sufficiently well, though, more experiments with industrial size specifications are needed. Our current work focuses on extending the approach to FSMs with symbolic inputs and outputs [23] and eventually to a more general type of EFSM [14].
References
Pomeranz, I., Sudhakar, M.R.: Test generation for multiple state-table faults in finite-state machines. IEEE Trans. Comput. 46(7), 783–794 (1997)
Poage, J.F., McCluskey, Jr., E.J.: Derivation of optimal test sequences for sequential machines. In: Proceedings of the IEEE 5th Symposium on Switching Circuits Theory and Logical Design, pp. 121–132 (1964)
DeMilli, R.A., Offutt, J.A.: Constraint-based automatic test data generation. IEEE Trans. Softw. Eng. 17(9), 900–910 (1991)
Grunsky, I.S., Petrenko, A.: Design of checking experiments with automata describing protocols. Automatic Control and Computer Sciences. Allerton Press Inc. USA. No. 4 (1988)
Hennie, F.C.: Fault detecting experiments for sequential circuits. In: Proceedings of the IEEE 5th Annual Symposium on Switching Circuits Theory and Logical Design. Princeton, pp. 95–110 (1964)
Koufareva, I., Petrenko, A., Yevtushenko, N.: Test generation driven by user–defined fault models. In: Proceedings of the 12th International Workshop on Testing of Communicating Systems, pp. 215–233 (1999)
Lee, D., Yannakakis, M.: Principles and methods of testing finite-state machines - a survey. Proc. IEEE 84(8), 1090–1123 (1996)
Moore, E.F.: Gedanken experiments on sequential machines. In: Automata Studies, pp. 129–153. Princeton University Press (1956)
Petrenko, A., Yevtushenko, N.: Test suite generation for a FSM with a given type of implementation errors. In: Proceedings of IFIP 12th International Symposium on Protocol Specification, Testing, and Verification, pp. 229–243 (1992)
Petrenko, A., Yevtushenko, N., Bochmann, G.V.: Fault models for testing in context. In: Gotzhein, R., Bredereke, J. (eds.) Formal Description Techniques IX, pp. 163–178. Springer, Heidelberg (1996)
Vasilevskii, M.P.: Failure diagnosis of automata. Cybernetics, vol. 4, pp. 653–665. Plenum Publishing Corporation, New York (1973)
Chow, T.S.: Testing software design modeled by finite-state machines. IEEE Trans. Softw. Eng. 4(3), 178–187 (1978)
Vuong, S.T., Ko, K.C.: A novel approach to protocol test sequence generation. In: Global Telecommunications Conference, vol. 3, pp. 2–5. EEE (1990)
Petrenko, A., Boroday, S., Groz, R.: Confirming configurations in EFSM testing. IEEE Trans. Softw. Eng. 30(1), 29–42 (2004)
de Moura, L., Bjørner, N.S.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008)
Bochmann, G.V., et al.: Fault models in testing. In: Proceedings of the IFIP TC6/WG6. 1 Fourth International Workshop on Protocol Test Systems. North-Holland Publishing Co., pp. 17–30 (1991)
Petrenko, A., Yevtushenko, N.: Testing from partial deterministic FSM specifications. IEEE Trans. Comput. 54(9), 1154–1165 (2005)
Petrenko, A., Dury, A., Ramesh, S., Mohalik, S.: A method and tool for test optimization for automotive controllers. In: ICST Workshops, pp. 198–207. IEEE (2013)
Parr, T.: The Definitive ANTLR 4 Reference, vol. 2. Pragmatic Bookshelf, Raleigh (2013)
Petrenko, A, Nguena Timo, O., Ramesh, S.: Multiple mutation testing from FSM. In: Proceedings of the 35th IFIP WG 6.1 International Conference on Formal Techniques for Distributed Objects, Components, and Systems, pp. 222–238 (2016)
Belli, F., Budnik, C.J., Hollmann, A., Tuglular, T., Wong, W.E.: Model-based mutation testing - approach and case studies. Sci. Comput. Programm. 120, 25–48 (2016)
El-Fakih, K., Dorofeeva, R., Yevtushenko, N., Bochmann, G.V.: FSM-based testing from user defined faults adapted to incremental and mutation testing. Programm. Comput. Softw. 38, 201–209 (2012)
Petrenko, A.: Checking experiments for symbolic input/output finite state machines. In: ICST Workshops, pp. 229–237. IEEE (2016)
Acknowledgements
This work is supported in part by GM, NSERC and MEIE of Gouvernement du Québec.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Petrenko, A., Timo, O.N., Ramesh, S. (2016). Test Generation by Constraint Solving and FSM Mutant Killing. In: Wotawa, F., Nica, M., Kushik, N. (eds) Testing Software and Systems. ICTSS 2016. Lecture Notes in Computer Science(), vol 9976. Springer, Cham. https://doi.org/10.1007/978-3-319-47443-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-47443-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47442-7
Online ISBN: 978-3-319-47443-4
eBook Packages: Computer ScienceComputer Science (R0)