Beyond Level Planarity

Abstract

In this paper we settle the computational complexity of two open problems related to the extension of the notion of level planarity to surfaces different from the plane. Namely, we show that the problems of testing the existence of a level embedding of a level graph on the surface of the rolling cylinder or on the surface of the torus, respectively known by the name of Cyclic Level Planarity and Torus Level Planarity, are polynomial-time solvable.

Moreover, we show a complexity dichotomy for testing the Simultaneous Level Planarity of a set of level graphs, with respect to both the number of level graphs and the number of levels.

Research was partially supported by DFG grant Ka812/17-1, by MIUR project AMANDA, prot. 2012C4E3KT_001, and by DFG grant WA 654/21-1.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction and Overview

The study of level drawings of level graphs has spanned a long time; the seminal paper by Sugiyama et al. on this subject [23] dates back to 1981, well before graph drawing was recognized as a distinguished research area. This is motivated by the fact that level graphs naturally model hierarchically organized data sets and level drawings are a very intuitive way to represent such graphs.

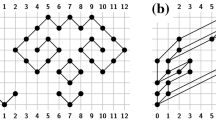
Formally, a level graph $(V,E,\gamma )$ is a directed graph (V, E) together with a function $\gamma : V \rightarrow \{1,\ldots ,k\}$, with $1 \le k \le |V|$. The set $V_i = \{ v \in V :\gamma (v)=i\}$ is the i-th level of $(V,E,\gamma )$. A level graph $(V,E,\gamma )$ is proper if for each $(u,v) \in E$, either $\gamma (u) = \gamma (v) - 1$, or $\gamma (u)=k$ and $\gamma (v)=1$. Let $l_1,\dots ,l_k$ be k horizontal straight lines on the plane ordered in this way with respect to the y-axis. A level drawing of $(V,E,\gamma )$ maps each vertex $v\in V_i$ to a point on $l_i$ and each edge $(u,v)\in E$ to a curve monotonically increasing in the y-direction from u to v. Note that a level graph $(V,E,\gamma )$ containing an edge $(u,v)\in E$ with $\gamma (u)>\gamma (v)$ does not admit any level drawing. A level graph is level planar if it admits a level embedding, i.e., a level drawing with no crossing; see Fig. 1(a). The Level Planarity problem asks to test whether a given level graph is level planar.

Fig. 1.

Level embeddings (a) on the plane, (b) on the standing cylinder, (c) on the rolling cylinder, and (d) on the torus.

Problem Level Planarity has been studied for decades [12, 15, 18, 20, 22], starting from a characterization of the single-source level planar graphs [12] and culminating in a linear-time algorithm for general level graphs [20]. A characterization of level planarity in terms of “minimal” forbidden subgraphs is still missing [13, 17]. The problem has also been studied to take into account a clustering of the vertices (Clustered Level Planarity [2, 14]) or consecutivity constraints for the vertex orderings on the levels ($\mathcal {T}$-level Planarity [2, 24]).

Differently from the standard notion of planarity, the concept of level planarity does not immediately extend to representations of level graphs on surfaces different from the plane¹. When considering the surface $\mathbb O$ of a sphere, level drawings are usually defined as follows: The vertices have to be placed on the k circles given by the intersection of $\mathbb O$ with k parallel planes, and each edge is a curve on $\mathbb O$ that is monotone in the direction orthogonal to these planes. The notion of level planarity in this setting goes by the name of Radial Level Planarity and is known to be decidable in linear time [4]. This setting is equivalent to the one in which the level graph is embedded on the “standing cylinder”: Here, the vertices have to be placed on the circles defined by the intersection of the cylinder surface $\mathbb S$ with planes parallel to the cylinder bases, and the edges are curves on $\mathbb S$ monotone with respect to the cylinder axis; see [3, 4, 10] and Fig. 1(b).

Problem Level Planarity has been also studied on the surface $\mathbb R$ of a “rolling cylinder”; see [3, 5, 6, 10] and Fig. 1(c). In this setting, k straight lines $l_1,\dots ,l_k$ parallel to the cylinder axis lie on $\mathbb R$, where $l_1,\dots ,l_k$ are seen in this clockwise order from a point p on one of the cylinder bases, the vertices of level $V_i$ have to be placed on $l_i$, for $i=1,\dots ,k$, and each edge (u, v) is a curve $\lambda$ lying on $\mathbb R$ and flowing monotonically in clockwise direction from u to v as seen from p. Within this setting, the problem takes the name of Cyclic Level Planarity [6]. Note that a level graph $(V,E,\gamma )$ may now admit a level embedding even if it contains edges (u, v) with $\gamma (u)>\gamma (v)$. Contrary to the other mentioned settings, the complexity of testing Cyclic Level Planarity is still unknown, and a polynomial (in fact, linear) time algorithm has been presented only for strongly connected graphs [5], which are level graphs such that for each pair of vertices there exists a directed cycle through them.

In this paper we settle the computational complexity of Cyclic Level Planarity by showing a polynomial-time algorithm to test whether a level graph admits a cyclic level embedding (Theorem 3). In order to obtain this result, we study a version of level planarity in which the surface $\mathbb T$ where the level graphs have to be embedded has genus 1; we call Torus Level Planarity the corresponding decision problem, whose study was suggested in [6]. It is not difficult to note (Lemmata 1 and 2) that the torus surface combines the representational power of the surfaces of the standing and of the rolling cylinder – that is, if a graph admits a level embedding on one of the latter surfaces, then it also admits a level embedding on the torus surface. Furthermore, both Radial Level Planarity and Cyclic Level Planarity (and hence Level Planarity) reduce in linear time to Torus Level Planarity.

The main result of the paper (Theorem 2) is a quadratic-time algorithm for proper instances of Torus Level Planarity and a quartic-time algorithm for general instances. Our solution is based on a linear-time reduction (Observation 1 and Lemmata 3–6) that, starting from any proper instance of Torus Level Planarity, produces an equivalent instance of the Simultaneous PQ-Ordering problem [8] that can be solved in quadratic time (Theorem 1).

Motivated by the growing interest in simultaneous embeddings of multiple planar graphs, which allow to display several relationships on the same set of entities in a unified representation, we define a new notion of level planarity in which multiple level graphs are considered and the goal is to find a simultaneous level embedding of them. The problem Simultaneous Embedding (see the seminal paper [11] and a recent survey [7]) takes as input k planar graphs $(V,E_1),\dots ,(V,E_k)$ and asks whether they admit planar drawings mapping each vertex to the same point of the plane. We introduce the problem Simultaneous Level Planarity, which asks whether k level graphs $(V,E_1,\gamma ),\dots ,(V,E_k,\gamma )$ admit level embeddings mapping each vertex to the same point along the corresponding level. As an instance of Simultaneous Level Planarity for two graphs on two levels is equivalent to one of Cyclic Level Planarity on two levels (Theorem 5), we can solve Simultaneous Level Planarity in polynomial time in this case. This positive result cannot be extended (unless P=NP), as the problem becomes NP-complete even for two graphs on three levels and for three graphs on two levels (Theorem 4). Altogether, this establishes a tight border of tractability for Simultaneous Level Planarity.

Complete proofs can be found in the full version of the paper [1].

2 Preliminaries

A tree T is a connected acyclic graph. The degree-1 vertices of T are the leaves of T, denoted by $\mathcal{L}(T)$, while the remaining vertices are the internal vertices.

A digraph $G=(V,E)$ without directed cycles is a directed acyclic graph (DAG). An edge $(u, v) \in E$ directed from u to v is an arc; vertex u is a parent of v and v is a child of u. A vertex is a source (sink) if it has no parents (children).

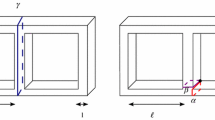
Embeddings on Levels. An embedding of a graph on a surface $\mathbb Q$ is a mapping $\varGamma$ of each vertex v to a distinct point on $\mathbb Q$ and of each edge $e=(u,v)$ to a simple Jordan curve on $\mathbb Q$ connecting u and v, such that no two curves cross except at a common endpoint. Let $\mathbb I$ and $\mathbb S^1$ denote the unit interval and the boundary of the unit disk, respectively. We define the surface $\mathbb S$ of the standing cylinder, $\mathbb R$ of the rolling cylinder, and $\mathbb T$ of the torus as $\mathbb S = \mathbb S^1 \times \mathbb I$, as $\mathbb R = \mathbb I \times \mathbb S^1$, and as $\mathbb T = \mathbb S^1 \times \mathbb S^1$, respectively. The j-th level of surfaces $\mathbb S$, $\mathbb R$, and $\mathbb T$ with k levels is defined as $l_j = \mathbb S^1 \times \{\frac{j-1}{k-1}\}$, $l_j = \mathbb I \times \{e^{2\pi i \frac{j-1}{k}}\}$, and $l_j = \mathbb S^1 \times \{e^{2\pi i \frac{j-1}{k}}\}$, respectively; see Fig. 2. An edge (x, y) on $\mathbb S$, on $\mathbb R$, or on $\mathbb T$ is monotone if it intersects the levels $\gamma (x), \gamma (x)+1, \dots , \gamma (y)$, where $k+1=1$, exactly once and does not intersect any of the other levels.

Fig. 2.

Levels on (a) $\mathbb S$, on (b) $\mathbb R$, and on (c) $\mathbb T$, respectively.

Problems Radial, Cyclic, and Torus Level Planarity take as input a level graph $G=(V,E,\gamma )$ and ask to find an embedding $\varGamma$ of G on $\mathbb S$, on $\mathbb R$, and on $\mathbb T$, respectively, in which each vertex $v \in V$ lies on $l_{\gamma (v)}$ and each edge $(u,v) \in E$ is monotone. Embedding $\varGamma$ is called a radial, a cyclic, and a torus level embedding of G, respectively. A level graph admitting a radial, cyclic, or torus level embedding is called radial, cyclic, or torus level planar, respectively.

Lemmata 1 and 2 show that the torus surface combines the power of representation of the standing and of the rolling cylinder. To strengthen this fact, we present a level graph in Fig. 3a that is neither radial nor cyclic level planar, yet it is torus level planar; note that the underlying (non-level) graph is also planar.

Lemma 1

Every radial level planar graph is also torus level planar. Further, Radial Level Planarity reduces in linear time to Torus Level Planarity.

Lemma 2

Every cyclic level planar graph is also torus level planar. Further, Cyclic Level Planarity reduces in linear time to Torus Level Planarity.

Fig. 3.

(a) A level graph that is neither cyclic nor radial level planar, yet it is torus level planar. (b) A radial level embedding $\varGamma$ of a level graph $(V_1 \cup V_2,E,\gamma )$ on two levels. Colors are used for edges incident to vertices of degree larger than one to illustrate that the edge ordering on E in $\varGamma$ is v-consecutive.

Orderings and PQ-Trees. Let A be a finite set. We call linear ordering any permutation of A. When considering the first and the last elements of the permutation as consecutive, we talk about circular orderings. Let $\mathcal O$ be a circular ordering on A and let $\mathcal{O}'$ be the circular ordering on $A' \subseteq A$ obtained by restricting $\mathcal O$ to the elements of $A'$. Then $\mathcal{O}'$ is a suborder of $\mathcal O$ and $\mathcal O$ is an extension of $\mathcal O'$. Let A and S be finite sets, let $\mathcal{O}' = s_1,s_2,\dots ,s_{|S|}$ be a circular ordering on S, let $\phi : S \rightarrow A$ be an injective map, and let $A' \subseteq A$ be the image of S under $\phi$; then $\phi (\mathcal{O}')$ denotes the circular ordering $\phi (s_1),\phi (s_2),\dots ,\phi (s_{|S|})$. We also say that a circular ordering $\mathcal{O}'$ on S is a suborder of a circular ordering $\mathcal O$ on A (and $\mathcal O$ is an extension of $\mathcal{O}'$) if $\phi (\mathcal{O'})$ is a suborder of $\mathcal{O}$.

An unrooted PQ-tree T is a tree whose leaves are the elements of a ground set A. PQ-tree T can be used to represent all and only the circular orderings $\mathcal{O}(T)$ on A satisfying a given set of consecutivity constraints on A, each of which specifies that a subset of the elements of A has to appear consecutively in all the represented circular orderings on A. The internal nodes of T are either P-nodes or Q-nodes. The orderings in $\mathcal{O}(T)$ are all and only the circular orderings on the leaves of T obtained by arbitrarily ordering the neighbours of each P-node and by arbitrarily selecting for each Q-node either a given circular ordering on its neighbours or its reverse ordering. Note that possibly $\mathcal{O}(T)=\emptyset$, if T is the empty tree, or $\mathcal{O}(T)$ represents all possible circular orderings on A, if T is a star centered at a P-node. In the latter case, T is the universal PQ-tree on A.

We illustrate three linear-time operations on PQ-trees (see [9, 16, 19]). Let T and $T'$ be PQ-trees on A and let $X\subseteq A$: The reduction of T by X builds a new PQ-tree on A representing the circular orderings in $\mathcal{O}(T)$ in which the elements of X are consecutive. The projection of T to X , denoted by $T|_X$, builds a new PQ-tree on X representing the circular orderings on X that are suborders of circular orderings in $\mathcal{O}(T)$. The intersection of T and $T'$, denoted by $T \cap T'$, builds a new PQ-tree on A representing the circular orderings in $\mathcal{O}(T) \cap \mathcal{O}(T')$.

Simultaneous PQ-Ordering. Let $D=(N,Z)$ be a DAG with vertex set $N=\{T_1,\dots ,T_k\}$, where $T_i$ is a PQ-tree, such that each arc $(T_i,T_j;\phi ) \in Z$ consists of a source $T_i$, of a target $T_j$, and of an injective map $\phi : \mathcal{L}(T_j) \rightarrow \mathcal{L}(T_i)$ from the leaves of $T_j$ to the leaves of $T_i$. Given an arc $a=(T_i,T_j;\phi ) \in Z$ and circular orderings $\mathcal{O}_i \in \mathcal{O}(T_i)$ and $\mathcal{O}_j \in \mathcal{O}(T_j)$, we say that arc a is satisfied by $(\mathcal{O}_i,\mathcal{O}_j)$ if $\mathcal{O}_i$ extends $\phi (\mathcal{O}_j)$. The Simultaneous PQ-Ordering problem asks to find circular orderings $\mathcal{O}_1 \in \mathcal{O}(T_1),\dots ,\mathcal{O}_k \in \mathcal{O}(T_k)$ on $\mathcal{L}(T_1),\dots ,\mathcal{L}(T_k)$, respectively, such that each arc $(T_i,T_j;\phi ) \in Z$ is satisfied by $(\mathcal{O}_i,\mathcal{O}_j)$.

Let $(T_i,T_j;\phi )$ be an arc in Z. An internal node $\mu _i$ of $T_i$ is fixed by an internal node $\mu _j$ of $T_j$ (and $\mu _j$ fixes $\mu _i$ in $T_i$) if there exist leaves $x,y,z \in \mathcal{L}(T_j)$ and $\phi (x),\phi (y),\phi (z) \in \mathcal{L}(T_i)$ such that (i) removing $\mu _j$ from $T_j$ makes x, y, and z pairwise disconnected in $T_j$, and (ii) removing $\mu _i$ from $T_i$ makes $\phi (x)$, $\phi (y)$, and $\phi (z)$ pairwise disconnected in $T_i$. Note that by (i) the three paths connecting $\mu _j$ with x, y, and z in $T_j$ share no node other than $\mu _j$, while by (ii) those connecting $\mu _i$ with $\phi (x)$, $\phi (y)$, and $\phi (z)$ in $T_i$ share no node other than $\mu _i$. Since any ordering $\mathcal{O}_j$ determines a circular ordering around $\mu _j$ of the paths connecting it with x, y, and z in $T_j$, any ordering $\mathcal{O}_i$ extending $\phi (\mathcal{O}_j)$ determines the same circular ordering around $\mu _i$ of the paths connecting it with $\phi (x)$, $\phi (y)$, and $\phi (z)$ in $T_i$; this is why we say that $\mu _i$ is fixed by $\mu _j$.

Theorem 1 below will be a key ingredient in the algorithms of the next section. However, in order to exploit it, we need to consider normalized instances of Simultaneous PQ-Ordering, namely instances $D=(N,Z)$ such that, for each arc $(T_i,T_j;\phi ) \in Z$ and for each internal node $\mu _j \in T_j$, tree $T_i$ contains exactly one node $\mu _i$ that is fixed by $\mu _j$. This property can be guaranteed by an operation, called normalization [8], defined as follows. Consider each arc $(T_i,T_j;\phi ) \in Z$ and replace $T_j$ with $T_i|_{\phi (\mathcal{L}(T_j))} \cap T_j$ in D, that is, replace tree $T_j$ with its intersection with the projection of its parent $T_i$ to the set of leaves of $T_i$ obtained by applying mapping $\phi$ to the leaves $\mathcal{L}(T_j)$ of $T_j$.

Consider a normalized instance $D=(N,Z)$. Let $\mu$ be a P-node of a PQ-tree T with parents $T_1,\dots ,T_r$ and let $\mu _i \in T_i$ be the unique node in $T_i$, with $1 \le i \le r$, fixed by $\mu$. The fixedness $fixed(\mu )$ of $\mu$ is defined as $fixed(\mu ) = \omega + \sum ^r_{i=1} (fixed(\mu _i)-1)$, where $\omega$ is the number of children of T fixing $\mu$. A P-node $\mu$ is k-fixed if $fixed(\mu ) \le k$. Also, instance D is k-fixed if all the P-nodes of any PQ-tree $T \in N$ are k-fixed.

Theorem 1

(Bläsius and Rutter [8], Theorems 3.2 and 3.3). 2-fixed instances of Simultaneous PQ-Ordering can be tested in quadratic time.

3 Torus Level Planarity

In this section we provide a polynomial-time testing and embedding algorithm for Torus Level Planarity that is based on the following simple observation.

Observation 1

A proper level graph $G=(\bigcup ^k_{i=1}V_i,E,\gamma )$ is torus level planar if and only if there exist circular orderings $\mathcal{O}_1,\dots ,\mathcal{O}_k$ on $V_1,\dots ,V_k$ such that, for each $1 \le i \le k$ with $k+1=1$, there exists a radial level embedding of the level graph $(V_i \cup V_{i+1},(V_i \times V_{i+1}) \cap E,\gamma )$ in which the circular orderings on $V_i$ along $l_i$ and on $V_{i+1}$ along $l_{i+1}$ are $\mathcal{O}_i$ and $\mathcal{O}_{i+1}$, respectively.

In view of Observation 1 we focus on a level graph $G=(V_1 \cup V_2,E,\gamma )$ on two levels $l_1$ and $l_2$. Denote by $V_1^+$ and by $V_{2}^-$ the subsets of $V_1$ and of $V_2$ that are incident to edges in E, respectively. Let $\varGamma$ be a radial level embedding of G. Consider a closed curve c separating levels $l_1$ and $l_2$ and intersecting all the edges in E exactly once. The edge ordering on E in $\varGamma$ is the circular ordering in which the edges in E intersect c according to a clockwise orientation of c on the surface $\mathbb S$ of the standing cylinder; see Fig. 3b. Further, let $\mathcal O$ be a circular ordering on the edge set E. Ordering $\mathcal O$ is vertex-consecutive (v-consecutive) if all the edges incident to each vertex in $V_1 \cup V_2$ are consecutive in $\mathcal O$.

Let $\mathcal O$ be a v-consecutive ordering on E. We define orderings $\mathcal{O}^+_1$ on $V_1^+$ and $\mathcal{O}^-_2$ on $V_2^-$ induced by $\mathcal{O}$, as follows. Consider the edges in E one by one as they appear in $\mathcal{O}$. Append the end-vertex in $V^+_1$ of the currently considered edge to a list $\mathcal{L}^+_1$. Since $\mathcal O$ is v-consecutive, the occurrences of the same vertex appear consecutively in $\mathcal{L}^+_1$, regarding such a list as circular. Hence, $\mathcal{L}^+_1$ can be turned into a circular ordering $\mathcal{O}^+_1$ on $V^+_1$ by removing repetitions of the same vertex. Circular ordering $\mathcal{O}^-_2$ can be constructed analogously. We have the following.

Lemma 3

Let $\mathcal O$ be a circular ordering on E and $(\mathcal{O}_1,\mathcal{O}_2)$ be a pair of circular orderings on $V_1$ and $V_2$. There exists a radial level embedding of G whose edge ordering is $\mathcal O$ and such that the circular orderings on $V_1$ and $V_2$ along $l_1$ and $l_2$ are $\mathcal{O}_1$ and $\mathcal{O}_2$, respectively, if and only if $\mathcal O$ is v-consecutive, and $\mathcal{O}_1$ and $\mathcal{O}_2$ extend the orderings $\mathcal{O}^+_1$ and $\mathcal{O}^-_2$ on $V_1^+$ and $V_2^-$ induced by $\mathcal O$, respectively.

Proof

The necessity is trivial. For the sufficiency, assume that $\mathcal O$ is v-consecutive and that $\mathcal{O}_1$ and $\mathcal{O}_2$ extend the orderings $\mathcal{O}^+_1$ and $\mathcal{O}^-_2$ on $V_1^+$ and $V_2^-$ induced by $\mathcal O$, respectively. We construct a radial level embedding $\varGamma$ of G with the desired properties, as follows. Let $\varGamma ^*$ be a radial level embedding consisting of |E| non-crossing curves, each connecting a distinct point on $l_1$ and a distinct point on $l_2$. We associate each curve with a distinct edge in E, so that the edge ordering of $\varGamma ^*$ is $\mathcal O$. Note that, since $\mathcal O$ is v-consecutive, all the occurrences of the same vertex of $V^+_1$ and of $V_2^-$ appear consecutively along $l_1$ and $l_2$, respectively. Hence, we can transform $\varGamma ^*$ into a radial level embedding $\varGamma '$ of $G'=(V_1^+ \cup V_2^-, E, \gamma )$, by continuously deforming the curves in $\varGamma ^*$ incident to occurrences of the same vertex in $V_1^+$ (in $V_2^-$) so that their end-points on $l_1$ (on $l_2$) coincide. Since the circular orderings on $V_1^+$ and on $V_2^-$ along $l_1$ and $l_2$ are $\mathcal{O}^+_1$ and $\mathcal{O}^-_2$, respectively, we can construct $\varGamma$ by inserting the isolated vertices in $V_1 \setminus V_1^+$ and $V_2 \setminus V_2^-$ at suitable points along $l_1$ and $l_2$, so that the circular orderings on $V_1$ and on $V_2$ along $l_1$ and $l_2$ are $\mathcal{O}_1$ and $\mathcal{O}_2$, respectively.   $\square$

We construct an instance I(G) of Simultaneous PQ-Ordering starting from a level graph $G=(V_1 \cup V_2,E,\gamma )$ on two levels as follows; refer to Fig. 4, where I(G) corresponds to the subinstance $I(G_{i,i+1})$ in the dashed box. We define the level trees $T_1$ and $T_2$ as the universal PQ-trees on $V_1$ and $V_2$, respectively. Also, we define the layer tree $T_{1,2}$ as the PQ-tree on E representing exactly the edge orderings for which a radial level embedding of G exists, which are the v-consecutive orderings on E, by Lemma 3. The PQ-tree $T_{1,2}$ can be constructed in O(|G|) time [9, 19]. We define the consistency trees $T_1^+$ and $T_2^-$ as the universal PQ-trees on $V_1^+$ and $V_2^-$, respectively. Instance I(G) contains $T_1$, $T_2$, $T_{1,2}$, $T_1^+$, and $T_2^-$, together with the arcs $(T_1, T_1^+, \iota )$, $(T_2, T_2^-, \iota )$, $(T_{1,2}, T_1^+, \phi _1^+)$, and $(T_{1,2}, T_2^-, \phi _{2}^-)$, where $\iota$ denotes the identity map and $\phi _1^+$ ($\phi _2^-$) assigns to each vertex in $V_1^+$ (in $V_2^-$) an incident edge in E. We have the following.

Fig. 4.

Instance $I^*(G)$ of Simultaneous PQ-Ordering for a level graph $G=(V,E,\gamma )$. Instance $I(G_{i,i+1})$ corresponding to the level graph $(V_i \cup V_{i+1}, (V_i \times V_{i+1}) \cap E, \gamma )$ induced by levels i and $i+1$ of G is enclosed in a dashed box.

Lemma 4

Level graph G admits a radial level embedding in which the circular ordering on $V_1$ along $l_1$ is $\mathcal{O}_1$ and the circular ordering on $V_2$ along $l_2$ is $\mathcal{O}_2$ if and only if instance I(G) of Simultaneous PQ-Ordering admits a solution in which the circular ordering on $\mathcal {L}(T_1)$ is $\mathcal{O}_1$ and the one on $\mathcal {L}(T_2)$ is $\mathcal{O}_2$.

Proof

We prove the necessity. Let $\varGamma$ be a radial level embedding of G. We construct an ordering on the leaves of each tree in I(G) as follows. Let $\mathcal{O}_1$, $\mathcal{O}_2$, $\mathcal{O}^+_1$, and $\mathcal{O}^-_2$ be the circular orderings on $V_1$ along $l_1$, on $V_2$ along $l_2$, on $V_1^+$ along $l_1$, and on $V_2^-$ along $l_2$ in $\varGamma$, respectively. Let $\mathcal{O}$ be the edge ordering on E in $\varGamma$. Note that $\mathcal{O}\in \mathcal{O}(T_{1,2})$ since $\mathcal{O}$ is v-consecutive by Lemma 3. The remaining trees are universal, hence $\mathcal{O}_{1}\in \mathcal{O}(T_{1})$, $\mathcal{O}_{2}\in \mathcal{O}(T_{2})$, $\mathcal{O}^+_{1}\in \mathcal{O}(T^+_{1})$, and $\mathcal{O}^-_{2}\in \mathcal{O}(T^-_{2})$.

We prove that all arcs of I(G) are satisfied. Arc $(T_1,T_1^+,\iota )$ is satisfied if and only if $\mathcal{O}_1$ extends $\mathcal{O}^+_1$. This is the case since $\iota$ is the identity map, since $V_1^+ \subseteq V_1$, and since $\mathcal{O}_1$ and $\mathcal{O}^+_1$ are the circular orderings on $V_1$ and $V_1^+$ along $l_1$. Analogously, arc $(T_2,T_2^-,\iota )$ is satisfied. Arc $(T_{1,2},T_1^+,\phi ^+_1)$ is satisfied if and only if $\mathcal{O}$ extends $\mathcal{O}^+_1$. This is due to the fact that $\phi ^+_1$ assigns to each vertex in $V_1^+$ an incident edge in E and to the fact that, by Lemma 3, ordering $\mathcal{O}$ is v-consecutive and $\mathcal{O}^+_1$ is induced by $\mathcal{O}$. Analogously, arc $(T_{1,2},T_{2}^-,\phi ^-_2)$ is satisfied.

We prove the sufficiency. Suppose that I(G) is a positive instance of Simultaneous PQ-Ordering, that is, there exist orderings $\mathcal{O}_1$, $\mathcal{O}_2$, $\mathcal{O}^+_1$, $\mathcal{O}^-_2$, and $\mathcal{O}$ of the leaves of the trees $T_1$, $T_2$, $T^+_1$, $T^-_2$, and $T_{1,2}$, respectively, satisfying all arcs of I(G). Since $\iota$ is the identity map and since arcs $(T_1,T_1^+,\iota )$ and $(T_2,T_2^-,\iota )$ are satisfied, we have that $\mathcal{O}^+_1$ and $\mathcal{O}^-_2$ are restrictions of $\mathcal{O}_1$ and $\mathcal{O}_2$ to $V_1^+$ and $V_2^-$, respectively. Also, since $(T_{1,2},T_1^+,\phi ^+_1)$ and $(T_{1,2},T_{2}^-,\phi ^-_2)$ are satisfied, we have that $\mathcal{O}$ extends both $\mathcal{O}^+_1$ and $\mathcal{O}^-_2$. By the construction of $T_{1,2}$, ordering $\mathcal{O}$ is v-consecutive. By Lemma 3, a radial level embedding $\varGamma$ of G exists in which the circular ordering on $V_i$ along $l_i$ is $\mathcal{O}_i$, for $i=1,2$.   $\square$

We now show how to construct an instance $I^*(G)$ of Simultaneous PQ-Ordering from a proper level graph $G=(\bigcup ^k_{i=1} V_i,E,\gamma )$ on k levels; refer to Fig. 4. For each $i=1,\dots ,k$, let $I(G_{i,i+1})$ be the instance of Simultaneous PQ-Ordering constructed as described above starting from the level graph on two levels $G_{i,i+1}=(V_i \cup V_{i+1}, (V_i \times V_{i+1}) \cap E, \gamma )$ (in the construction $V_i$ takes the role of $V_1$, $V_{i+1}$ takes the role of $V_2$, and $k+1=1$). Any two instances $I(G_{i-1,i})$ and $I(G_{i,i+1})$ share exactly the level tree $T_i$, whereas non-adjacent instances are disjoint. We define $I^\cup (G)= \bigcup ^k_{i=1} I(G_{i,i+1})$ and obtain $I^*(G)$ by normalizing $I^\cup (G)$. We now present two lemmata about properties of instance $I^*(G)$.

Lemma 5

$I^*(G)$ is 2-fixed, has O(|G|) size, and can be built in O(|G|) time.

Proof

Every PQ-tree T in $I^\cup (G)$ is either a source with exactly two children or a sink with exactly two parents, and the normalization of $I^\cup (G)$ to obtain $I^*(G)$ does not alter this property. Thus every P-node in a PQ-tree T in $I^*(G)$ is at most 2-fixed. In fact, recall that for a P-node $\mu$ of a PQ-tree T with parents $T_1,\dots ,T_r$, we have that $fixed(\mu ) = \omega + \sum ^r_{i=1} (fixed(\mu _i)-1)$, where $\omega$ is the number of children of T fixing $\mu$, and $\mu _i \in T_i$ is the unique node in $T_i$, with $1 \le i \le r$, fixed by $\mu$. Hence, if T is a source PQ-tree, it holds $\omega = 2$ and $r=0$; whereas, if T is a sink PQ-tree, it holds $\omega = 0$, $r=2$, and $fixed(\mu _i)=2$ for each parent $T_i$ of T. Therefore $I^*(G)$ is 2-fixed.

Since every internal node of a PQ-tree in $I^*(G)$ has degree greater than 2, to prove the bound on $|I^*(G)|$ it suffices to show that the total number of leaves of all PQ-trees in $I^*(G)$ is in O(|G|). Since $\mathcal{L}(T_i)=V_i$ and $\mathcal{L}(T^-_i),\mathcal{L}(T^+_i)\subseteq V_i$, the number of leaves of all level and consistency trees is at most $3\sum _{i=1}^k |V_i|\in O(|G|)$. Also, since $\mathcal{L}(T_{i,i+1})= (V_i \times V_{i+1}) \cap E$, the number of leaves of all layer trees is at most $\sum _{i=1}^k |(V_i \times V_{i+1}) \cap E|\in O(|G|)$. Thus $|I^*(G)|\in O(|G|)$.

We have already observed that each layer tree $T_{i,i+1}$ can be constructed in $O(|G_{i,i+1}|)$ time; level and consistency trees are stars, hence they can be constructed in linear time in the number of their leaves. Finally, the normalization of each arc $(T_i,T_j; \phi )$ can be performed in $O(|T_i|+|T_j|)$ time [8]. Hence, the O(|G|) time bound follows.   $\square$

Lemma 6

Level graph G admits a torus level embedding if and only if $I^*(G)$ is a positive instance of Simultaneous PQ-Ordering.

Proof

Suppose that G admits a torus level embedding $\varGamma$. For $i=1,\dots ,k$, let $\mathcal{O}_i$ be the circular ordering on $V_i$ along $l_i$. By Observation 1, embedding $\varGamma$ determines a radial level embedding $\varGamma _{i,i+1}$ of $G_{i,i+1}$. By Lemma 4, for $i=1,\dots ,k$, there exists a solution for the instance $I(G_{i,i+1})$ of Simultaneous PQ-Ordering in which the circular ordering on $\mathcal{L}(T_i)$ ($\mathcal{L}(T_{i+1})$) is $\mathcal{O}_i$ (resp. $\mathcal{O}_{i+1}$). Since the circular ordering on $\mathcal{L}(T_i)$ is $\mathcal{O}_i$ both in $I(G_{i-1,i})$ and $I(G_{i,i+1})$ and since each arc of $I^*(G)$ is satisfied as it belongs to exactly one instance $I(G_{i,i+1})$, which is a positive instance of Simultaneous PQ-Ordering, it follows that the circular orderings deriving from instances $I(G_{i,i+1})$ define a solution for $I^*(G)$.

Suppose that $I^*(G)$ admits a solution. Let $\mathcal{O}_1,\dots ,\mathcal{O}_k$ be the circular orderings on the leaves of the level trees $T_1,\dots ,T_k$ in this solution. By Lemma 4, for each $i=1,\dots , k$ with $k+1=1$, there exists a radial level embedding of level graph $G_{i,i+1}$ in which the circular orderings on $V_i$ along $l_i$ and $V_{i+1}$ along $l_{i+1}$ are $\mathcal{O}_{i}$ and $\mathcal{O}_{i+1}$, respectively. By Observation 1, G is torus level planar.   $\square$

We thus get the main result of this paper.

Theorem 2

Torus Level Planarity can be tested in quadratic (quartic) time for proper (non-proper) instances.

Proof

Consider any instance G of Torus Level Planarity. Assume first that G is proper. By Lemmata 5 and 6, a 2-fixed instance $I^*(G)$ of Simultaneous PQ-Ordering equivalent to G can be constructed in linear time with $|I^*(G)| \in O(|G|)$. By Theorem 1 instance $I^*(G)$ can be tested in quadratic time.

If G is not proper, then subdivide every edge (u, v) that spans $h>2$ levels with $h-2$ vertices, assigned to levels $\gamma (u)+1,\gamma (u)+2,\dots ,\gamma (v)-1$. This increases the size of the graph at most quadratically, and the time bound follows.   $\square$

Theorem 2 and Lemma 2 imply the following result.

Theorem 3

Cyclic Level Planarity can be solved in quadratic (quartic) time for proper (non-proper) instances.

Our techniques allow us to solve a more general problem, that we call Torus $\mathcal T$-Level Planarity, in which a level graph $G=(\bigcup ^k_{i=1} V_i,E,\gamma )$ is given together with a set of PQ-trees $\mathcal{T}=\{\overline{T}_1,\dots ,\overline{T}_k\}$ such that $\mathcal{L}(\overline{T}_i)= V_i$, where each tree $\overline{T}_i$ encodes consecutivity constraints on the ordering on $V_i$ along $l_i$. The goal is then to test the existence of a level embedding of G on $\mathbb T$ in which the circular ordering on $V_i$ along $l_i$ belongs to $\mathcal{O} (\overline{T}_i)$. This problem has been studied in the plane [2, 24] under the name of $\mathcal T$-Level Planarity; it is NP-hard in general and polynomial-time solvable for proper instances. While the former result implies the NP-hardness of Torus $\mathcal T$-Level Planarity, the techniques of this paper show that Torus $\mathcal T$-Level Planarity can be solved in polynomial time for proper instances. Namely, in the construction of instance $I^*(G)$ of Simultaneous PQ-Ordering, it suffices to replace level tree $T_i$ with PQ-tree $\overline{T}_i$. Analogous considerations allow us to extend this result to Radial $\mathcal T$-Level Planarity and Cyclic $\mathcal T$-Level Planarity.

4 Simultaneous Level Planarity

In this section we prove that Simultaneous Level Planarity is NP-complete for two graphs on three levels and for three graphs on two levels, while it is polynomial-time solvable for two graphs on two levels.

Both NP-hardness proofs rely on a reduction from the NP-complete problem Betweenness [21], which asks for a ground set S and a set X of ordered triplets of S, with $|S|=n$ and $|X|=k$, whether a linear order $\prec$ of S exists such that, for any $(\alpha ,\beta ,\gamma ) \in X$, it holds true that $\alpha \prec \beta \prec \gamma$ or that $\gamma \prec \beta \prec \alpha$. Both proofs exploit the following gadgets.

The ordering gadget is a pair of level graphs on levels $l_1$ and $l_2$, where $l_1$ contains nk vertices $u_{i,j}$, with $i=1,\dots ,k$ and $j=1,\dots ,n$, and $l_2$ contains $n (k-1)$ vertices $v_{i,j}$, with $i=1,\dots ,k-1$ and $j=1,\dots ,n$. For $i=1,\dots ,k-1$ and $j=1,\dots ,n$, contains edge $(u_{i,j},v_{i,j})$ and contains edge $(u_{i+1,j},v_{i,j})$. See and in Fig. 5(a). Consider any simultaneous level embedding $\varGamma$ of and assume, w.l.o.g. up to a renaming, that $u_{1,1},\dots ,u_{1,n}$ appear in this left-to-right order along $l_1$.

Lemma 7

For every $i=1,\dots ,k$, vertices $u_{i,1},\dots ,u_{i,n}$ appear in this left-to-right order along $l_1$ in $\varGamma$; also, for every $i=1,\dots ,k-1$, vertices $v_{i,1},\dots ,v_{i,n}$ appear in this left-to-right order along $l_2$ in $\varGamma$.

The triplet gadget is a path $T=(w_1,\dots ,w_5)$ on two levels, where $w_1$, $w_3$, and $w_5$ belong to a level $l_i$ and $w_2$ and $w_4$ belong to a level $l_j\ne l_i$. See in Fig. 5(a), with $i=1$ and $j=2$. We have the following.

Lemma 8

In every level embedding of T, vertex $w_3$ is between $w_1$ and $w_5$ along $l_i$.

We are now ready to prove the claimed NP-completeness results.

Fig. 5.

Instances (a) and (b) corresponding to an instance of Betweenness with $X=\{(u_{1,1},u_{1,2},u_{1,4}),(u_{1,2},u_{1,3},u_{1,4}),(u_{1,1},u_{1,3},u_{1,4})\}$.

Theorem 4

Simultaneous Level Planarity is NP-complete even for three graphs on two levels and for two graphs on three levels.

Proof

Both problems clearly are in $\mathcal {NP}$. We prove the $\mathcal {NP}$-hardness only for three graphs on two levels (see Fig. 5(a)), as the other proof is analogous (see Fig. 5(b)). We construct an instance of Simultaneous Level Planarity from an instance $(S=\{u_{1,1},\dots ,u_{1,n}\},X=\{(u_{1,a_i},u_{1,b_i},u_{1,c_i}):i=1,\dots ,k\})$ of Betweenness as follows: Pair contains an ordering gadget on levels $l_1$ and $l_2$, where the vertices $u_{1,1},\dots ,u_{1,n}$ of are (in bijection with) the elements of S. Graph contains k triplet gadgets $T_i(u_{i,a_i},x_i,u_{i,b_i},y_i,u_{i,c_i})$, for $i=1,\dots ,k$. Vertices $x_1,y_1,\dots ,x_k,y_k$ are all distinct and are on $l_2$. Clearly, the construction can be carried out in linear time. We prove the equivalence of the two instances.

$(\Longrightarrow )$ Suppose that a simultaneous level embedding $\varGamma$ of exists. We claim that the left-to-right order of $u_{1,1},\dots ,u_{1,n}$ along $l_1$ satisfies the betweenness constraints in X. Suppose, for a contradiction, that there exists a triplet $(u_{1,a_i},u_{1,b_i},u_{1,c_i})\in X$ with $u_{1,b_i}$ not between $u_{1,a_i}$ and $u_{1,c_i}$ along $l_1$. By Lemma 7, $u_{i,b_i}$ is not between $u_{i,a_i}$ and $u_{i,c_i}$. By Lemma 8, we have that $T_i(u_{i,a_i},x_i,u_{i,b_i},y_i,u_{i,c_i})$ is not planar in $\varGamma$, a contradiction.

$(\Longleftarrow )$ Suppose that (S, X) is a positive instance of Betweenness, and assume, w.l.o.g. up to a renaming, that $\prec :=u_{1,1},\dots ,u_{1,n}$ is a solution for (S, X). Construct a straight-line simultaneous level planar drawing of with: (i) vertices $u_{1,1},\dots ,u_{1,n},$ $\dots , u_{k,1},$ $\dots ,u_{k,n}$ in this left-to-right order along $l_1$, (ii) vertices $v_{1,1},\dots ,v_{1,n},\dots ,v_{k-1,1},$ $\dots ,v_{k-1,n}$ in this left-to-right order along $l_2$, (iii) vertices $x_i$ and $y_i$ to the left of vertices $x_{i+1}$ and $y_{i+1}$, for $i=1,\dots ,k-1$, and (iv) vertex $x_i$ to the left of vertex $y_i$ if and only if $u_{1,a_i}\prec u_{1,c_i}$.

Properties (i) and (ii) guarantee that, for any two edges $(u_{i,j},v_{i,j})$ and $(u_{i',j'},v_{i',j'})$, vertex $u_{i,j}$ is to the left of $u_{i',j'}$ along $l_1$ if and only if $v_{i,j}$ is to the left of $v_{i',j'}$ along $l_2$, which implies the planarity of in $\varGamma$. The planarity of in $\varGamma$ is proved analogously. Properties (i) and (iii) imply that no two paths $T_i$ and $T_j$ cross each other, while Property (iv) guarantees that each path $T_i$ is planar. Hence, the drawing of in $\varGamma$ is planar.   $\square$

The graphs in Theorem 4 can be made connected, by adding vertices and edges, at the expense of using one additional level. Also, the theorem holds true even if the simultaneous embedding is geometric or with fixed edges (see [7, 11] for definitions).

In contrast to the NP-hardness results, a reduction to a proper instance of Cyclic Level Planarity allows us to decide in polynomial time instances composed of two graphs on two levels. Namely, the edges of a graph are directed from $l_1$ to $l_2$, while those of the other graph are directed from $l_2$ to $l_1$.

Theorem 5

Simultaneous Level Planarity is quadratic-time solvable for two graphs on two levels.

5 Conclusions and Open Problems

In this paper we have settled the computational complexity of two of the main open problems in the research topic of level planarity by showing that the Cyclic Level Planarity and the Torus Level Planarity problems are polynomial-time solvable. Our algorithms run in quartic time in the graph size; it is hence an interesting challenge to design new techniques to improve this time bound. We also introduced a notion of simultaneous level planarity for level graphs and we established a complexity dichotomy for this problem.

An intriguing research direction is the one of extending the concept of level planarity to surfaces with genus larger than one. However, there seems to be more than one meaningful way to arrange k levels on a high-genus surface. A reasonable choice would be the one shown in the figure, in which the levels are arranged in different sequences between two distinguished levels $l_s$ and $l_t$ (and edges only connect vertices on two levels in the same sequence). Radial Level Planarity and Torus Level Planarity can be regarded as special cases of this setting (with only one and two paths of levels between $l_s$ and $l_t$, respectively).