Abstract
This work presents a hybrid strategy for optimization of Capacitated Vehicle Routing Problem (CVRP) that employs Genetic Algorithms (GA) combined with the heuristics of Gillett & Miller (GM) and Hill Climbing (HC). The first heuristic is used to incorporate feasible solutions in the initial population of the GA while the second is responsible for the refinement of solutions after a certain number of generations without improvements. The computational experiments showed that the proposed strategy presented good results for the optimization of CVRP with respect to the quality of solutions well as the computational cost.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The optimization of production processes in the industrial environment has been an object of study and research in various areas of knowledge, such as business management, economics, logistics, among others, being most notably studied in production engineering [1, 2]. In logistics, for example, the distribution of products and routing of vehicles are gaining space and becoming competitive advantages for companies. To reduce the delivery time, increasing the availability of products and inputs, it is mandatory to make deliveries respecting the deadlines. Nevertheless, the reduction of costs associated with the vehicles routing activity becomes an important tool for effective planning of products distribution.
The Vehicle Routing Problem (VRP) has attracted, in the last years, an increasing attention of researchers due to the great difficulty of its solution and its presence in many practical applications [3]. As consequence, there has been great effort to develop robust algorithms that can be modeled according to the scenario that describes a determined situation.
The Capacitated Vehicle Routing Problem is a variant of VRP and consists, basically, in determining the routes to be followed by a fleet of homogeneous vehicles, to serve a given number of customers, without violating the capacities of the vehicles [4]. The CVRP belongs to the class of NP-hard problems, that is, problems whose the solution usually requires non-polynomial complexity time algorithms and because of this are usually solved with the use of heuristic and metaheuristics algorithms such as Gillett & Miller [5], Clarke and Wright [6, 7], Tabu Search [6, 8], Simulated Annealing [6] and Genetic Algorithms [9, 10].
This work presents a strategy for CVRP optimization using Genetic Algorithms combined with two heuristics: Gillett & Miller and Hill Climbing. The first one is used to generate solutions that are included in the initial population of GA, starting it with some feasible solutions while the second is responsible for making a refinement of the solutions generated by the GA, after a certain number of generations without improvement. It is worth mentioning that among the works available in the literature, we did not find approaches using the constructive and refinement heuristics considered in this work combined with GA for solving CVPR.
The performed experiments showed that the proposed strategy presented good results for CVRP solution, confirming that the use of the employed heuristics helps the GA to converge on promising points in the search space with a smaller number of generations.
2 Theoretical Background
2.1 Capacitated Vehicle Routing Problem
The CVRP is the classic version of VRP in which all customers have their demands previously defined and that must be attended entirely by a only vehicle, the fleet is homogeneous, in other words, all vehicles are similar and run from only distribution center. In this problem, just the vehicle capacity restriction is imposed [6]. This restriction determines that the sum of the demand of all customers of a route does not exceed the capacity of vehicle used to execute that route.
Let G = (V, A) be a graph in which V = 0.....,n is the set of vertices that represent the customers and A the set of edges, representing the connections among the customers and the distribution center.
Each edge \((v_i,v_j)\) is associated with a cost, \(C_{ij}\), representing the cost of the connection between the vertices i and j. When \(C_{ij} = C_{ji}\), the problem is recognized as symmetrical, otherwise the problem is identified as asymmetrical. A set of K identical vehicles with capacity cv is allocated to the distribution center. For each customer vi a demand di is associated, and for the distribution center is defined d\(_{0}\) = 0.
In summary, the CVRP consists of finding a set of routes, where each route is traveled by a vehicle, with the objective of minimizing the total cost of the routes (tc), respecting the following restrictions: (i) Each route must start and finish at the distribution center; (ii) Each customer must be visited just only time and (iii) The sum of the customers’ demands included in a route can not exceed the vehicle’s capacity. The mathematical formulation of CVRP, adapted from Vieira [11], is expressed as follows:
Minimize
Subject to
where: \(d_i\): demand of customer i; k: vehicle; K: set of vehicles; S: Set of customers; nc: number of customers; v(S): Minimum number of vehicles to attend S; cv: Capacity of vehicles; \(c_{ij}\): cost of the connection from vertex i to vertex j; tc: is the total cost of routes (Eq. 1); \(x_{ijk}\): connection from the vertex i to vertex j with vehicle k;
Equation 2 ensures that K vehicles will be used starting from the distribution center, while the Eq. 3 guarantees that each route has its beginning and ending at the distribution center. Equation 4 defines that customers must be attended exactly one time and the Eq. 5 keeps the flow ensuring that the vehicle arrives at a customer and out of it, preventing that a route ends prematurely. The Eq. 6 prevents the formulation of routes which do not include the distribution center. In this restriction, v(S) represents the minimum number of vehicles required to attend a set of customers S.
To ensure that the number of vehicles used to attend the set customers of S is not less than v(S), the restriction 6 establishes, indirectly, that the capacity of the vehicle is not exceeded. However to let explicit, the Eq. 7 is used to formulate the capacity restriction. The Eq. 8 is related to the dimensions and allowed values of matrix x. The Eq. 9 is used to evaluate the solutions generated by the proposed strategy. It reflects the value of the objective function (OF) or fitness and involves the number of vehicles used in the solution, the violated restrictions (Eqs. 2 to 7) and the total cost of routes.
where: \(W_v\) is the weight assigned to the number of vehicles used in the solution; nr is the Number of violated restrictions and \(W_r\) is the weight given to the violated restrictions.
2.2 Heuristics and Metaheuristic Techniques Employed by Proposed Approach
Genetic Algorithms (GA) are probabilistic search methods that are based on the evolutionary process, in other words, based on the theory of species evolution proposed by Charles Darwin [10]. GA present the following operational steps: starts a population containing a predefined number of individuals, in which each individual represents a possible solution. For each individual is attributed a value of aptitude or fitness, in our case represented by Eq. 9, which indicates how good is the individual in relation to the population. Thereby, individuals are selected based on their aptitudes and pass their characteristics to the next generation. To this end, it is applied the crossover and mutation methods between individuals, aiming the development of a new generation with fittest individuals (best solutions). This iterative process is repeated until the stopping criterion is reached [9].
The algorithm of Gillett & Miller [5] is based on the notion of economies and is part of the group of two stages heuristics (or constructive heuristics). The strategy consists in dividing the problem in two steps to solve it. In the first step, the vertices (points of demands) are grouped according to some criterion of proximity. Then, the routes are obtained by solution of CVRP for each of the formed groups of vertices [12].
The Hill Climbing algorithm is a local search technique based on depth [13]. It adjusts the position of a candidate solution (state) only if the new position (neighbor) is better than the current state. In other words, the optimization of this algorithm occurs by evaluating neighboring solutions of current state, based on their objective function values. At each step, the solution generated by the current state is replaced by the solution represented by the best neighbor and the algorithm terminates when it reaches a peak (or a valley when it is trying to minimize a fitness function), that is, when it did not find better solution in the neighborhood [14]. Due to the characteristics of this algorithm, it has been used for refining of solutions generated by metaheuristics, in solving several problems. In additon, when this algorithm is applied in a minimization problem, as CVPR addressed in this work, it is also referred as “downhill”.
3 Methodology
For development of proposed strategy, the programming language C/C++ and GAlib libraryFootnote 1 were used. The GAlib is a free library widely used in solving combinatorial optimization problems. To evaluate the strategy, experiments were performed and the results obtained were compared with the best results found in the literature, for the sets of instances from Christofides [15] and TSPLIBFootnote 2 with up to 30 customers. In the experiments, the following hardware configurations were used: Intel Celeron 2955U, 1.40 GHz processor; 4 GB of RAM; operating system Windows 7 Ultimate 32-bits.
4 Proposed Strategy for CVRP Optimization
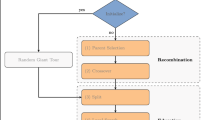
In the proposed strategy (illustrated in Fig. 1), it was decided to represent the chromosome by a binary matrix with dimensions nc x nc x K, in which rows represent the number of customers to be visited, columns represent the order that customers will be visited and K, the number of vehicles (fleet). A chromosome is a solution contemplating customers information which will be attended by some vehicle, including customer visiting order. This representation facilitates the control of the restrictions imposed on the problem an also the execution of GA operations such as crossover and mutation.
In the refinement process by HC algorithm, the neighborhood of a current state (solution) is generated by shifting the elements of chromosome’s matrix in a circular manner along the two dimensions indicated by nc (rows/columns), considering four directions (up, down, left and right). The parameters used by GA were defined (empirically) as follows: Chromosome encoding = Binary Matrix; Population Size = 1200; Population subset for refinement (R) = 1/3 of population; Number of generations without improvement (gw) = 30; Number of Generations (used as stop criterion) = 5000; Population rate of replacement = 80%; Elitism = 20%; Crossover = 80%; Selection Method = Roulette; Rate of Mutation = 1%; Type of Mutation = Flip Bit.
5 Results and Discussion
In the evaluation of the proposed strategy, we performed ten tests for each of 16 considered instances and the results obtained were compared with the best solutions in the literature. For instances of Christofides [15], the optimal solutions presented by Reinelt and Wenger [16] were considered and for TSPLIB instances, the optimal solutions indicated by Ralphs et al. [17] were adopted.
To evaluate the goodness of the solutions obtained, a measure known in the literature as GAP was used. In our case, GAP = (OF_Med - OF_Best) OF_Best, being OF_Med the average of the objective function (OF) values obtained in the 10 tests (using Eq. 9) and OF_best the OF value of the best solution found in the literature. In addition, the standard deviation of OF values (\(OF_\sigma \)), the execution time and the best solution (OF*) obtained by our strategy, for each instance, are presented in Table 1. Nevertheless, we present in Table 2 the results of proposed strategy evaluation, with and without the use of heuristics Gillett & Miller and Hill Climbing were performed in a combined way, as follows: GA + GM + HC = Genetic Algorithms + Gillett & Miller + Hill Climbing; GA + GM = Genetic Algorithms + Gillett & Miller; GA + HC = Genetic Algorithms + Hill Climbing; GM = only Gillett & Miller; GA = Only Genetic Algorithms (without the use of heuristics).
As can be seen in Table 1, the GAP in most cases (exception of instances “E-n13-k4”, and “E-n23-k3”) remained less than 10% and, for 38% of instances, the strategy found the best known solution (OF_Best). In addition, for 69% of instances the obtained GAP was less or equal than 5%.
The Table 1 also shows that the average GAP considering the 16 instances did not exceed 5%, showing the good performance of the strategy with respect to the quality of the solutions. It is also possible to observe that the standard deviation (\(OF_\sigma \)) in 81% of cases is less than 10 and, in 50% of the cases, it was obtained \(OF_\sigma \) less than 5, indicating good stability strategy with respect to the exploitation of the search space. Concerning the computational cost, the processing time ranges from 80 seconds to smaller instance (Eil7) to 250 seconds for larger instances (Eil30 and E-n30-k3). Thus, this strategy showed the relatively low computational cost. However, this processing time could be improved minimizing the sparsity of chromosome representation.
Table 2 shows a comparison of the results obtained by the proposed strategy with and without the application of considered heuristics (GM and HC). Note that, in general, the results are better when these heuristics are embedded in GA. These results suggest that the use of heuristics Gillett & Miller and Hill Climbing helps the GA to converge for promising points in the search space, creating solutions with good quality.
6 Conclusions and Outlook
In this work, a hybrid strategy for solving the Capacitated Vehicle Routing Problem (CVRP) using Genetic Algorithms (GA) combined with the heuristics of Gillett & Miller (GM) and Hill Climbing (HC) was presented. From the computational experiments, it was possible to conclude that the proposed strategy achieved good results with re-spect to quality of solutions with low computational cost, considering the instances extracted from Christofides and TSPLIB libraries. The experiments also demonstrate that the use of heuristics Gillett & Miller and Hill Climbing helped the GA to converge on promising points in the search space with a smaller number of generations.
References
Kunnathur, A.S., Sundararaghavan, P., Sampath, S.: Dynamic rescheduling using a simulation-based expert system. J. Manufact. Technol. Manag. 15(2), 199–212 (2004)
Heinonen, J., Pettersson, F.: Hybrid ant colony optimization and visibility studies applied to a job-shop scheduling problem. Appl. Math. Comput. 187(2), 989–998 (2007)
Cordeau, J.F., Laporte, G., Potvin, J.Y., Savelsbergh, M.W.: Chapter 7 transportation on demand. In: Barnhart, C., Laporte, G. (eds.) Transportation, Handbooks in Operations Research and Management Science, vol. 14, pp. 429–466. Elsevier, Amsterdam (2007)
Xu, H., Chen, Z.L., Rajagopal, S., Arunapuram, S.: Solving a practical pickup and delivery problem. Transp. Sci. 37(3), 347–364 (2003)
Gillett, B.E., Miller, L.R.: A heuristic algorithm for the vehicle-dispatch problem. Oper. Res. 22(2), 340–349 (1974)
Laporte, G.: The vehicle routing problem: an overview of exact and approximate algorithms. Eur. J. Oper. Res. 59(3), 345–358 (1992)
Laporte, G., Gendreau, M., Potvin, J.Y., Semet, F.: Classical and modern heuristics for the vehicle routing problem. Int. Trans. Oper. Res. 7(4–5), 285–300 (2000)
Cordeau, J.F., Laporte, G.: Tabu Search Heuristics for the Vehicle Routing Problem. Technical report (2002)
Holland, J., Goldberg, D.: Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley, Reading (1989)
Bjarnadóttir, Á.S.: Solving the vehicle routing problem with genetic algorithms. Ph.D. thesis, Technical University of Denmark, DTU, DK-2800 Kgs. Lyngby, Denmark (2004)
Vieira, H.P.: Metaheuristica para a Solução de Problemas de Roteamento de Veículos com Janela de Tempo. Ph.D. thesis, Instituto de Matemática, Estatística e Computação Científica, Universidade Estadual de Campinas (2008)
Goldbarg, M.C., Luna, H.P.L.: Otimização Combinatória e Programação Linear: Modelos e Algoritmos, vol. 2. Elsevier, Amsterdam (2005)
Engelbrecht, A.P.: Fundamentals of Computational Swarm Intelligence. Wiley, Hoboken (2006)
Russell, S., Norvig, P., Intelligence, A.: A Modern Approach: Artificial Intelligence. Prentice-Hall, Egnlewood Cliffs (1995)
Christofides, N.: Vehicle Routing. A Guided Tour of Combinatorial Optimization. Wiley, New York (1985)
Reinelt, G., Wenger, K.M.: Maximally violated mod-p cuts for the capacitated vehicle-routing problem. INFORMS J. Comput. 18(4), 466–479 (2006)
Ralphs, T., Pulleyblank, W., Trotter Jr., L.: On capacitated vehicle routing. In: Problem, Mathematical Programming (1998)
Acknowledgments
The authors would like to thank UNINOVE by financial support.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Lima, S.J.d.A., Santos, R.A.R., Alves de Araujo, S., Triguis Schimit, P.H. (2016). Combining Genetic Algorithm with Constructive and Refinement Heuristics for Solving the Capacitated Vehicle Routing Problem. In: Nääs, I., et al. Advances in Production Management Systems. Initiatives for a Sustainable World. APMS 2016. IFIP Advances in Information and Communication Technology, vol 488. Springer, Cham. https://doi.org/10.1007/978-3-319-51133-7_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-51133-7_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51132-0
Online ISBN: 978-3-319-51133-7
eBook Packages: Computer ScienceComputer Science (R0)