Abstract
Customer order fulfillment at distribution centers (DC) is increasingly necessitated by innovative strategies to maximize operational performance that are primarily driven by cost and service level under supply chain variability. In order to better understand the trade-offs, in this paper, a generic computational model is developed to estimate forklift travel times for DCs with any arbitrary floor space and loading docks. In particular, travel times are modelled as random variables and the moments of the probability distribution of travel times are estimated and used as inputs to analytical queueing model and discrete event simulation model. Results show that the analytical and simulation models are within 3% under different demand scenarios. These models are used to determine the impact of work-force capacity on key performance measures such as Truck Processing Time (TPT) and Labor Hours Per Truck (LHPT). The workforce capacity for different demand scenarios is determined using three different approaches - Target Utilization Level, Square Root Staffing (SRS) rule (adapted from call center staffing) and Optimization. The result from these models indicate that adapting workforce capacity to match varying demand can reduce cost by 18% while maintaining desired service level.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Supply chain variability can be caused by product seasonality, batch production and transportation, product consolidation or value added processing. DCs buffer the material flow in supply chains to accommodate this variability. Incoming items brought to the DC are unloaded at the receiving docks (receiving) and put into storage (storing). Outgoing items are retrieved from storage (order picking), processed and shipped to customers through the shipping docks (shipping). Resources such as space, labor, and equipment are allocated to different DC functions following organizational policies to achieve desired operational performance in terms of capacity, throughput and service at minimum cost. DCs can adapt to varying demand by adjusting workforce capacity to meet desired service level [1, 2].
Several authors had investigated the effects of warehouse design and control on operational performance and developed analytical and simulation models for performance analysis. Pandit and Palekar investigated the effects of warehouse design on response time and suggested a method for optimal design based on response time [3]. Chew and Tang presented a travel time model that evaluates performance of an order picking system with consideration to order batching and storage allocation strategies [4]. Graves et al. evaluated warehouse performance for several sequencing and class based storage policies using continuous analytical models and discrete evaluation procedures [5]. Bozer and White modelled the performance of an end-of-aisle order picking system by deriving analytical expressions and developed a design algorithm to determine the optimal configuration [6]. Koster proposed a modeling and approximate analysis method for a pick-to-belt order picking system based on Jackson network modeling and analysis [7]. Lee presented an analytical method for the stochastic analysis of a unit load AS/RS [8]. Hur et al. presented an analytical model for the stochastic analysis of a unit load AS/RS without assuming any specific distribution for the travel time of the S/R machine [9]. The existing literature has predominantly focused on warehouse design and control using travel time models and performance analysis in terms of throughput, resource utilization and storage strategy for order picking systems. As labor cost can be a significant component of variable cost in DCs, it is evident that there is a need for research to explore the impact of workforce capacity on DC performance by considering cost and service level trade-off for varying demand scenarios. This work has been motivated by paucity of models and tools that can be used by DC operations managers for workforce planning in practice. Hence, a decision model that integrates critical operational performance measures to evaluate DC performance and workforce capacity policies under varying demand scenarios is developed.
2 Model and Assumptions
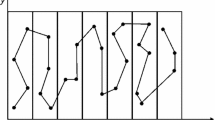
A large scale, non-automated, rectangular DC is analyzed. A rectangular shape is the optimal geometrical shape for storing rectangular units such as pallets [10]. The storage locations are characterized by single-deep racks and drive-in racks. The racks are arranged back-to-back, to form a block, parallel to the dock of the DC, such that space between blocks form aisles. The blocks are arranged in a rectangular grid to form a network of aisles through which material handling devices such as forklifts travel as shown in Fig. 1(a) [3]. A generic computational model with length (L), width (W), aisle-width (A) and number of docks (N) as parameters is developed to estimate forklift travel times in DCs. The model is capable to evaluate DCs with a size between 60,000 sq.ft (small scale) and 500,000 sq.ft. (large scale) and up to 45 docks. A probability distribution is fit to the forklift travel times and moments of the distribution is provided as input to the analytical queueing model of DC. The skewness profile of forklift travel time distribution against distance from center dock and L and W of the DC is investigated. It is observed that for a given W, skewness profile is represented by a series of peaks and valleys with decreasing value as L increases and for a given L, skewness profile remains nearly constant as W increases as shown in Fig. 1(b). The skewness for forklift travel time distributions fluctuate significantly from dock 1 (end dock) and becomes negligible towards dock 23 (center dock) and remains negligible from the center dock to dock 45 (end dock) as shown in Fig. 2.
2.1 DC Queueing System
The outbound operations in the DC begins by “accumulation” of customer orders from storage area as pallet loads in the dock to form a truck load. The pallet loads then undergo a “wrapping” process to secure items in the pallet after accumulation. The pallet loads are then “inspected” to verify that items in the pallets have completed all processes before loading. Pallets are then “loaded” onto the truck for shipping. The process time associated with accumulation, wrapping, inspection and loading are denoted by Accumulation Time (AT) or Forklift Travel Time, Wrapping Time (WT), Inspection Time (IT) and Loading Time (LT) respectively. The process time for a truck load, denoted by Truck Processing Time (TPT), is the sum of AT, WT, IT and LT. The operational productivity is expressed by a metric called Labor Hours Per Truck (LHPT). The movement of pallets are done using forklifts and pallet jacks. It is assumed that forklifts perform only accumulation operations and pallet jacks are used by wrapping team, inspection team and loading team for wrapping, inspection and loading respectively. The queueing model is shown in Fig. 3. The analytical queueing model facilitates development and evaluation of workforce capacity policies for the DC for several demand scenarios by providing a performance estimate for each policy-scenario combination.
2.2 DC Analytical Queueing Model
This system can be modelled as an open network queueing system with a First Come First Serve (FCFS) queue discipline and an infinite queue space. The customer orders for accumulation arrive at a rate ra in the form of palletized truck loads. Forklifts, wrapping team, inspection team and loading team act as servers. The system is characterized by a series of G/G/m queues for accumulation, wrapping, inspection and loading with general interarrival and process time distributions. The following parameters are provided as input to the analytical queueing model: ra - rate of arrivals in truck load per unit time; u - Workforce Utilization; ta - Average time between arrivals (in minute); ca - Arrival CV; cd - Departure CV; te - Mean effective process time (in minute); ce - CV of effective process time. The performance of the queueing system is characterized by the following parameters and are considered as the output from the analytical queueing model: m - Workforce level in a process; CTq - Expected waiting time in queue for a process (in minute); CT - Expected time for a process (in minute); TPT - Truck Processing Time (in minute); WIP - Average work-in-process level at process (in truck load); WIPq - Expected WIP in queue (in truck load); ATL - Average Truck Load; LHPT - Labor Hours Per Truck [11].
3 Performance Analysis Using Analytical Models
The workforce capacity of the DC is analyzed for several demand scenarios that range from a low demand to a high demand for a given process time at 70% target workforce utilization for all the process using the analytical queueing model. It is concluded that TPT decreases steadily as workforce capacity increases and LHPT increases linearly with workforce capacity as shown in Fig. 4(a) and (b). This establishes that as more workforce is deployed to process a truck load, the time to process the truck load decreases (service level improves) but labor hour investment on a truck load increases (cost increases).
The Square Root Staffing (SRS) rule is applied in call centers to determine the appropriate staffing levels for an offered load (R) and Quality of Service, (\(\beta \)) and is approximated as R + \(\beta \)VR, where, R is the amount of work that arrives in the system in unit time. The value of \(\beta \) signifies the operational regime of the system and can be a Quality Driven (QD) regime with emphasis on service level over efficiency, Efficiency Driven (ED) with emphasis on efficiency over service level or Quality Efficiency Driven (QED) regime with trade-off between service level and efficiency. Larger the \(\beta \) value, better the service level [12, 13].
The workforce capacity the DC queueing system is computed by the application of SRS rule for ED (\(\beta = 0\)), QD (\(\beta = 1\)) and QED (\(\beta = 0.5\)) operational regimes. It is observed that workforce capacity increases steadily as DC operates from an ED regime towards a QD regime as shown in Fig. 5. This implies that as more workforce is deployed to process a truck load, the service level of DC improves.
4 Performance Analysis Using Simulation Model
The DC queueing system is modelled using Simio simulation software for a given interarrival and process time distribution and workforce capacity. The DC simulation model is run for 500 h with 30 replications after a warm-up period of 100 h. The results from simulation model is compared with that of the analytical queueing model. The analytical and simulation model results for cycle time and workforce utilization are highly comparable as shown in Fig. 6(a) and (b). The TPT and LHPT are determined with −3.13% and −6.49% error respectively from the simulation model with reference to the analytical queueing model.
A simulation-based multi-objective optimization model is developed using OptQuest for Simio add-in. The optimal scenarios for workforce capacity that minimizes TPT and operating cost subject to constraints for a target workforce utilization policy is determined using pattern frontier optimization.
Minimize: TPT and Operating Cost subject to:
-
1 \(\le \) Forklift \(\ge \) 25
-
1 \(\le \) Wrapping Team \(\ge \) 6
-
1 \(\le \) Inspection Team \(\ge \) 8
-
1 \(\le \) Loading Team \(\ge \) 10
-
u \(\le \) 0.70
OptQuest optimizes across all responses and finds the set of scenarios that are optimal, rather than a single optimal solution based on weights, [15]. The model is run for 500 h after a warm-up period of 100 h with 30 replications for 100 scenarios. It is observed that there are six optimal scenarios with TPT, LHPT and operating cost that range between 628.24 min, 340 labor hours & 5915.95 and 689.66 min, 279 labor hours and 5000.07 respectively corresponding to a workforce capacity that range between 43 to 33 as shown in Fig. 7. It can be concluded from the optimal scenarios that the desired service level can be maintained by adapting workforce capacity to match demand and thereby reducing operating cost by up to 18%.
5 Conclusions
A decision model is developed to evaluate the impact of workforce capacity on DC performance in terms of Truck Processing Time and Labor Hours Per Truck by considering cost and service level trade-off for varying demand scenarios. Industrial practitioners can use this model for tactical and operational decisions in DCs by application and integration of travel time computation model, analytical and/or simulation model based on the DC geometry considered. The desired service level can be maintained and opportunities to reduce operating cost can be identified by adapting workforce capacity to match demand. Delays in truck processing significantly impacts detention time, the time spent waiting for a truck to be loaded. Increased detention time implies lost revenue by paying late fees to the shipper or missing an opportunity to secure another load. The models can facilitate industrial practitioners to negotiate for better pricing and terms of contract by reducing detention time substantially. The models presented in this work can be extended to automated DC with conveyors and the resulting energy footprint can be estimated [14, 15]. Ongoing work is focusing on implementing these models in a userfriendly spreadsheet tools for industrial practitioners.
References
Gu, J., Goetschalckx, M., McGinnis, L.F.: Research on warehouse operation: a comprehensive review. Eur. J. Oper. Res. 177(1), 1–21 (2007)
Rouwenhorst, B., Reuter, B., Stockrahm, V., van Houtum, G.J., Mantel, R.J., Zijm, W.H.M.: Warehouse design and control: framework and literature review. Eur. J. Oper. Res. 122(3), 515–533 (2000)
Pandit, R., Palekar, U.S.: Response time considerations for optimal warehouse layout design. J. Eng. Ind 115(3), 322–328 (1993)
Chew, E.P., Tang, L.C.: Travel time analysis for general item location assignment in a rectangular warehouse. Eur. J. Oper. Res. 112(3), 582–597 (1999)
Graves, S.C., Hausman, W.H., Schwarz, L.B.: Storage-retrieval interleaving in automatic warehousing systems. Manag. Sci. 23(9), 935–945 (1977)
Bozer, Y.A., White, J.A.: Design and performance models for end-of-aisle order picking systems. Manag. Sci. 36(7), 852–866 (1990)
Koster, R.: Performance approximation of pick-to-belt order picking systems. Eur. J. Oper. Res. 72(3), 558–573 (1994)
Lee, H.F.: Performance analysis for automated storage and retrieval systems. IIE Trans. 29(1), 15–28 (1997)
Hur, S., Lee, Y.H., Lim, S.Y., Lee, M.H.: A performance estimation model for AS/RS by M/G/1 queuing system. Comput. Ind. Eng. 46(2), 233–241 (2004)
Berry, J.R.: Elements of warehouse layout. Int. J. Prod. Res. 7(2), 105–121 (1968)
Hopp, W.J., Spearman, M.L.: Factory Physics, 3rd edn. Waveland Press Inc., Long Grove (2011)
Technion Israel Institute of Technology: http://ie.technion.ac.il/serveng/
Mandelbaum, A., Zeltyn, S.: Service engineering in action: the Palm/Erlang-A queue, with applications to call centers. In: Spath, D., Dipl.-Math, H., Fähnrich, K.P. (eds.) Advances in Services Innovations, pp. 17–45. Springer, Berlin (2007)
Krishna, A.G.: Workforce planning models for distribution center operations. Ph.D. thesis, State College, The Pennsylvania State University (2009)
Anand, V., Lee, S., Prabhu, V.V.: Energy-aware models for warehousing operations. In: Grabot, B., Vallespir, B., Gomes, S., Bouras, A., Kiritsis, D. (eds.) APMS 2014. IAICT, vol. 439, pp. 390–397. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44736-9_48
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Krishna, A.G., Prabhu, V.V. (2016). Workforce Planning Models for Distribution Center Operations. In: Nääs, I., et al. Advances in Production Management Systems. Initiatives for a Sustainable World. APMS 2016. IFIP Advances in Information and Communication Technology, vol 488. Springer, Cham. https://doi.org/10.1007/978-3-319-51133-7_25
Download citation
DOI: https://doi.org/10.1007/978-3-319-51133-7_25
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51132-0
Online ISBN: 978-3-319-51133-7
eBook Packages: Computer ScienceComputer Science (R0)