Abstract
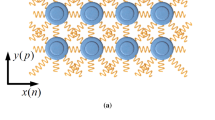
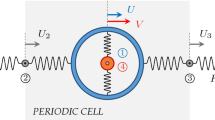
The dispersive wave propagation in a periodic metamaterial with tetrachiral topology and inertial local resonators is investigated. The Floquet-Bloch spectrum of the metamaterial is compared with that of the tetrachiral beam lattice material without resonators. The resonators can be designed to open and shift frequency band gaps, that is, spectrum intervals in which harmonic waves do not propagate. Therefore, an optimal passive control of the frequency band structure can be pursued in the metamaterial. To this aim, suitable constrained nonlinear optimization problems on compact sets of admissible geometrical and mechanical parameters are stated. According to functional requirements, sets of parameters which determine the largest low-frequency band gap between selected pairs of consecutive branches of the Floquet-Bloch spectrum are soughted for numerically. The various optimization problems are successfully solved by means of a version of the method of moving asymptotes, combined with a quasi-Monte Carlo multi-start technique.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The moving asymptotes [16] are asymptotes of functions (changing when moving from one optimization subproblem to the successive one), which are used to approximate (typically nonlinearly) the original objective and constraint functions.
- 2.
In a preliminary phase, we also considered as objective function a weighted sum, with positive weights, of the full band gap between the third and fourth dispersion curves and the band amplitude of the fourth dispersion curve. However, for various choices of the weights, the obtained solution was characterized by a negligible value either of the full band gap, or of the band amplitude, making an optimal choice of the weights difficult. For our specific goal, instead, the product of the two terms was more effective.
References
Bacigalupo, A., Gambarotta, L.: Homogenization of periodic hexa- and tetra-chiral cellular solids. Compos. Struct. 116, 461–476 (2014)
Bacigalupo, A., De Bellis, M.L.: Auxetic anti-tetrachiral materials: equivalent elastic properties and frequency band-gaps. Compos. Struct. 131, 530–544 (2015)
Bacigalupo, A., Gambarotta, L.: Simplified modelling of chiral lattice materials with local resonators. Int. J. Solids Struct. 83, 126–141 (2016)
Bacigalupo A., Lepidi M.: A lumped mass beam model for the wave propagation in anti-tetrachiral periodic lattices. In: XXII AIMETA Congress, Genoa, Italy (2015)
Bacigalupo, A., Lepidi, M.: High-frequency parametric approximation of the Floquet-Bloch spectrum for anti-tetrachiral materials. Int. J. Solids Struct. 97, 575–592 (2016)
Bacigalupo, A., Lepidi, M., Gnecco, G., Gambarotta, L.: Optimal design of auxetic hexachiral metamaterials with local resonators. Smart Mater. Struct. 25(5), 054009 (2016)
Bigoni, D., Guenneau, S., Movchan, A.B., Brun, M.: Elastic metamaterials with inertial locally resonant structures: application to lensing and localization. Phys. Rev. B 87, 174303 (2013)
Brillouin, L.: Wave Propagation in Periodic Structures, 2nd edn. Dover, New York (1953)
Gnecco, G., Sanguineti, M.: Regularization techniques and suboptimal solutions to optimization problems in learning from data. Neural Comput. 22, 793–829 (2010)
Gnecco, G., Gori, M., Sanguineti, M.: Learning with boundary conditions. Neural Comput. 25, 1029–1106 (2013)
Lepidi M., Bacigalupo A.: Passive control of wave propagation in periodic anti-tetrachiral metamaterials. In: VII European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Hersonissos, Crete Island (2016)
Liu, X.N., Hu, G.K., Sun, C.T., Huang, G.L.: Wave propagation characterization and design of two-dimensional elastic chiral metacomposite. J. Sound Vib. 330, 2536–2553 (2011)
Niederreiter H.: Random number generation and Quasi-Monte Carlo methods. SIAM (1992)
Phani, A.S., Woodhouse, J., Fleck, N.A.: Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 119, 1995–2005 (2006)
Spadoni, A., Ruzzene, M., Gonnella, S., Scarpa, F.: Phononic properties of hexagonal chiral lattices. Wave Motion 46, 435–450 (2009)
Svanberg, K.: The method of moving asymptotes - a new method for structural optimization. Int. J. Numer. Meth. Eng. 24, 359–373 (1987)
Svanberg, K.: A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J. Optim. 12, 555–573 (2002)
Tan, K.T., Huang, H.H., Sun, C.T.: Optimizing the band gap of effective mass negativity in acoustic metamaterials. Appl. Phys. Lett. 101, 241902 (2012)
Tee, K.F., Spadoni, A., Scarpa, F., Ruzzene, M.: Wave propagation in auxetic tetrachiral honeycombs. J. Vib. Acoust. ASME 132, 031007–1/8 (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Bacigalupo, A., Gnecco, G., Lepidi, M., Gambarotta, L. (2016). Design of Acoustic Metamaterials Through Nonlinear Programming. In: Pardalos, P., Conca, P., Giuffrida, G., Nicosia, G. (eds) Machine Learning, Optimization, and Big Data. MOD 2016. Lecture Notes in Computer Science(), vol 10122. Springer, Cham. https://doi.org/10.1007/978-3-319-51469-7_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-51469-7_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51468-0
Online ISBN: 978-3-319-51469-7
eBook Packages: Computer ScienceComputer Science (R0)