Abstract
In this paper, we show, almost constructively, a density theorem for hierarchies of limit spaces over separable metric spaces. Our proof is not fully constructive, since it relies on the constructively not acceptable fact that the limit relation induced by a metric space satisfies Urysohn’s axiom for limit spaces. By adding the condition of strict positivity to Normann’s notion of probabilistic projection we establish a relation between strictly positive general probabilistic selections on a sequential space and general approximation functions on a limit space. Showing that Normann’s result, that a (general and strictly positive) probabilistic selection is definable on a separable metric space, admits a constructive proof, and based on the constructively shown in [18] cartesian closure property of the category of limit spaces with general approximations, our quite effective density theorem follows. This work, which is a continuation of [18], is within computability theory at higher types and Normann’s Program of Internal Computability.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
This is a result of Hannes Diener (personal communication).
- 2.
If \((x_{n})_{n \in {{\mathbb {N}}}} \subseteq X\), for simplicity we write \(\lim _{X}(x, x_{n})\) instead of \(\lim _{X}(x, (x_{n})_{n \in {{\mathbb {N}}}})\), and \(\lim _{X}(x, x)\) instead of \(\lim _{X}(x, (x))\).
- 3.
Namely, the continuity condition used by Normann is different from the condition \((P_{3})\) used here, but one can show that they are equivalent. Since no continuity condition affects the main density theorem, we do not include here the proof of their equivalence.
- 4.
This principle is generally accepted within \(\mathrm {BISH}\) (see [3], p. 12).
- 5.
If \(c, d \in {{\mathbb {R}}}\), we use the notations \(c \vee d := \max \{c, d\}\), and \(c \wedge d := \min \{c, d\}\).
- 6.
The argument for the case of two positive numbers is the one used in the inductive step of the induction on n. If \(c_{1}, c_{2} > 0\), there are rationals \(q_{1}, q_{2}\) such that \(0< q_{1} < c_{1}\) and \(0< q_{2} < c_{2}\) (see [2], p. 25). Since \(q_{1} \wedge q_{2}\) is either \(q_{1}\) or \(q_{2}\), we get that \(q_{1} \wedge q_{2} < c_{1}\) and \(q_{1} \wedge q_{2} < c_{2}\), hence \(0 < q_{1} \wedge q_{2} \le c_{1} \wedge c_{2}\).
- 7.
Classically, this is trivial, since there is some \(j \in \{1, \ldots , n\}\) such that \(d(x, A_{n}) = d(x, a_{j})\), hence
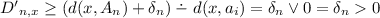 .
. - 8.
The proof is based on the fact that if \(c \le a\) and \(c \le b\), then \(c \le a \wedge b\), since if \(c > a \wedge b\), then \(c > a\) or \(c > b\) (this is the dual of a property of the maximum of real numbers included in [4], p. 57, Ex. 3).
- 9.
If \(c \vee 0 > 0\), then \(c> 0 \vee 0 > 0\) (see [4], p. 57). Hence, \(c > 0\) is the case, and then we get immediately that \(c \vee 0 = c\).
- 10.
Where the notion of approximation, as it is expressed in condition \((A_{3})\) of Definition 2, will depend on the structure of X.
References
Bishop, E.: Foundations of Constructive Analysis. McGraw-Hill, New York (1967)
Bishop, E., Bridges, D.: Constructive Analysis. Springer, Heidelberg (1985)
Bridges, D., Richman, F.: Varieties of Constructive Mathematics. University Press, Cambridge (1987)
Bridges, D.S., Vîţă, L.S.: Techniques of Constructive Analysis. Universitext. Springer, New York (2006)
DeJaeger, F.: Calculabilité sur les réels. Thesis, Paris VII (2003)
Dugundji, J.: Topology. Universal Book Stall, New Delhi (1990)
Hyland, M.: Recursion theory on the countable functionals. Dissertation, Oxford (1975)
Kuratowski, K.: Topology, vol. I. Academic Press, New York (1966)
Kuratowski, K.: Topology, vol. II. Academic Press, New York (1968)
Longley, J., Normann, D.: Higher-Order Computability. Springer, Heidelberg (2015)
Normann, D.: External and internal algorithms on the continuous functionals. In: Metakides, G. (ed.) Patras Logic Symposion, pp. 137–144. North-Holland Publishing Company, Amsterdam (1982)
Normann, D.: Internal density theorems for hierarchies of continuous functionals. In: Beckmann, A., Dimitracopoulos, C., Löwe, B. (eds.) CiE 2008. LNCS, vol. 5028, pp. 467–475. Springer, Heidelberg (2008). doi:10.1007/978-3-540-69407-6_50
Normann, D.: A rich hierarchy of functionals of finite types. Logical Methods Comput. Sci. 5(3:11), 1–21 (2009)
Normann, D.: Experiments on an internal approach to typed algorithms in analysis. In: Cooper, S.B., Sorbi, A. (eds.) Computability in context: computation and logic in the real world, pp. 297–327. Imperial College Press, London (2011)
Normann, D.: Banach spaces as data types. Logical Methods Comput. Sci. 7(2:11), 1–20 (2011)
Normann, D.: The continuous functionals as limit spaces. In: Berger, U., Diener, H., Schuster, P., Seisenberger, M. (eds.) Logic, Construction, Computation Mathematical Logic, vol. 3, pp. 353–379. Ontos, Heusenstamm (2012)
Petrakis, I.: Limit spaces in computability at higher types, manuscript (2013)
Petrakis, I.: Limit spaces with approximations. Ann. Pure Appl. Logic 167(9), 737–752 (2016)
Scarpellini, B.: A model for barrecursion of higher types. Compositio Mathematica 23(1), 123–153 (1971)
Acknowledgments
We would like to thank Ulrich Berger for his insightful comments on an early draft of this paper and Hannes Diener for informing us on his result that relates Urysohn’s axiom to LPO. We also thank the reviewers for their useful comments and suggestions and the Excellence Initiative of the LMU Munich for supporting our research.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Petrakis, I. (2017). A Density Theorem for Hierarchies of Limit Spaces over Separable Metric Spaces. In: Gopal, T., Jäger , G., Steila, S. (eds) Theory and Applications of Models of Computation. TAMC 2017. Lecture Notes in Computer Science(), vol 10185. Springer, Cham. https://doi.org/10.1007/978-3-319-55911-7_35
Download citation
DOI: https://doi.org/10.1007/978-3-319-55911-7_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-55910-0
Online ISBN: 978-3-319-55911-7
eBook Packages: Computer ScienceComputer Science (R0)



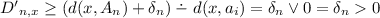 .
.