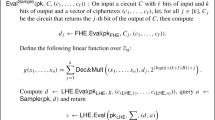Robust Transforming Combiners from Indistinguishability Obfuscation to Functional Encryption

Abstract

Indistinguishability Obfuscation (iO) has enabled an incredible number of new and exciting applications. However, our understanding of how to actually build secure iO remains in its infancy. While many candidate constructions have been published, some have been broken, and it is unclear which of the remaining candidates are secure.

This work deals with the following basic question: Can we hedge our bets when it comes to iO candidates? In other words, if we have a collection of iO candidates, and we only know that at least one of them is secure, can we still make use of these candidates?

This topic was recently studied by Ananth, Jain, Naor, Sahai, and Yogev [CRYPTO 2016], who showed how to construct a robust iO combiner: Specifically, they showed that given the situation above, we can construct a single iO scheme that is secure as long as (1) at least one candidate iO scheme is a subexponentially secure iO, and (2) either the subexponential DDH or LWE assumptions hold.

In this work, we make three contributions:

• (Better robust iO combiners.) First, we work to improve the assumptions needed to obtain the same result as Ananth et al.: namely we show how to replace the DDH/LWE assumption with the assumption that subexponentially secure one-way functions exist.

• (Transforming Combiners from iO to FE and NIKE.) Second, we consider a broader question: what if we start with several iO candidates where only one works, but we don’t care about achieving iO itself, rather we want to achieve concrete applications of iO? In this case, we are able to work with the minimal assumption of just polynomially secure one-way functions, and where the working iO candidate only achieves polynomial security. We call such combiners transforming combiners. More generally, a transforming combiner from primitive A to primitive B is one that takes as input many candidates of primitive A, out of which we are guaranteed that at least one is secure and outputs a secure candidate of primitive B. We can correspondingly define robust transforming combiners. We present transforming combiners from indistinguishability obfuscation to functional encryption and non-interactive multiparty key exchance (NIKE).

• (Correctness Amplification for iO from polynomial security and one-way functions.) Finally, along the way, we obtain a result of independent interest: Recently, Bitansky and Vaikuntanathan [TCC 2016] showed how to amplify the correctness of an iO scheme, but they needed subexponential security for the iO scheme and also require subexponentially secure DDH or LWE. We show how to achieve the same correctness amplification result, but requiring only polynomial security from the iO scheme, and assuming only polynomially secure one-way functions.

P. Ananth—This work was partially supported by grant #360584 from the Simons Foundation and the grants listed under Amit Sahai.

A. Jain—This work was supported by the grants listed under Amit Sahai.

A. Sahai—Research supported in part from a DARPA/ARL SAFEWARE award, NSF Frontier Award 1413955, NSF grants 1619348, 1228984, 1136174, and 1065276, BSF grant 2012378, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through the ARL under Contract W911NF-15-C-0205. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.

1 Introduction

Indistinguishability Obfuscation (iO), first defined by [4], has been a major revelation to cryptography. The discovery of the punctured programming technique by Sahai and Waters [46] has led to several interesting applications of indistinguishability obfuscation. A very incomplete list of such results includes functional encryption [2, 24, 47], the feasibility of succinct randomized encodings [7, 13, 39], time lock puzzles [8], software watermarking [16], instantiating random oracles [34] and hardness of Nash equilibrium [10, 26].

On the construction side, however, iO is still at a nascent stage. The first candidate was proposed by Garg et al. [24] from multilinear maps [19, 23, 29]. Since then there have many proposals of iO [3, 29, 48]. All these constructions are based on multilinear maps. The constructions of multilinear maps have come under scrutiny after several successful cryptanalytic attacks [14, 15, 17, 18, 35, 44] were mounted against them. In fact, there have also been direct attacks on some of the iO candidates as well [17, 44]. However, there are (fortunately) still many candidates that have survived all known cryptanalytic attacks. We refer the reader to Appendix A in [1] for a partial list of these candidates¹. In light of this, its imperative to revisit the applications of iO and hope to weaken the trust we place on any specific known iO candidate to construct these applications.

In other words, can we hedge our bets when it comes to iO candidates?

If we’re wrong about some candidates that seem promising right now, but not others, then can we still give explicit constructions that achieve the amazing applications of iO?

Robust iO Combiners. Recently, Ananth et al. [1] considered the closely related problem of constructing an iO scheme starting from many iO candidates, such that the final iO scheme is guaranteed to be secure as long as even one of the iO candidates is secure. In fact, they only assume that the secure candidate satisfies correctness, and in particular, the insecure candidates could also be incorrect. This notion is termed as a robust iO combiners (also studied by Fischlin et al. [22] in a relaxed setting where multiple underlying iO candidates must be secure) and are useful in constructing universal iO [32] ². The work of [1] constructs robust iO combiners assuming the existence of a sub-exponentially secure iO scheme and sub-exponentially secure DDH/ LWE. As a consequence of this result, we can construct the above applications by combining all known iO candidates as long as one of the candidates is sub-exponentially secure.

While the work of [1] is a major advance, it leaves open two very natural questions, that we study in this work. The first question is: do we really need to assume DDH or LWE? In other words:

1. What assumption suffices to construct a robust iO combiner?

In particular, are (sub-exponentially secure) one-way functions sufficient?

The second, broader, question is: if we care about constructing applications of iO, can we do better in terms of assumptions? In particular, recent work [27] has shown that functional encryption – itself an application of iO – can be directly used to construct several applications of iO. Let us then define an transforming combiner as an object that takes several iO candidates, with the promise that at least one of them is only polynomially secure, and outputs an explicit secure functional encryption scheme. Then, let us consider the following question, which truly addresses a minimal assumption:

2. Assuming only polynomially secure one-way functions, can we construct a transforming combiner from iO to functional encryption?

Note that since the existence of iO does not even imply that P $\ne$ NP, while functional encryption implies one-way functions, the above question lays out a minimal assumption for constructing a transforming combiner from iO to FE.

1.1 Our Contribution

We address questions 1 and 2 in this work. We show,

Theorem 1

(Transforming Combiners). Given many iO candidates out of which at least one of them is correct and secure and additionally assuming one-way functions, we can construct a compact functional encryption scheme.

As a corollary, we can construct an explicit functional encryption scheme assuming the existence of iO and one-way functions. In other words, we show that it suffices that iO exists (rather than relying on a constructive proof of it) to construct an explicit functional encryption scheme.

Corollary 1

(Informal). Assuming polynomially secure iO and one-way functions exists, we can construct an explicit compact functional encryption scheme. In particular, the construction of functional encryption does not rely on an explicit description of the iO scheme.

Combining this result with the works of [2, 11] who show how to construct iO from sub-exponentially secure compact FE, we obtain the following result.

Theorem 2

(Informal). There exists a robust iO combiner assuming sub-exponentially secure one-way functions as long as one of the underlying iO candidates is sub-exponentially secure.

This improves upon the result of Ananth et al. [1] who achieve the same result assuming sub-exponentially secure DDH or LWE.

Explicit NIKE from several iO candidates: Recent works of Garg and Srinivasan [28], Li and Micciancio [41], show how to achieve collusion resistant functional encryption from compact functional encryption and Garg et al. [27] show how to build multi-party non interactive key exchange (NIKE) from collusion resistant functional encryption. When combined with these results, our work shows how to obtain an explicit NIKE protocol when given any one-way function, and many iO candidates with the guarantee that only one of the candidates is secure.

New Correctness Amplification Theorem for iO. En route to achieving this result, we demonstrate a new correctness amplification theorem for iO. In particular, we show how to obtain almost-correct iO starting from polynomially secure approximately-correct iO³ and one-way functions. Prior to our work, [12] showed how to achieved a correctness amplification theorem starting from sub-exponentially secure iO and sub-exponentially secure DDH/ LWE.

Theorem 3

(Informal). There is a transformation from a polynomially secure approximately-correct iO to polynomially secure almost-correct iO assuming one-way functions.

2 Technical Overview

The goal of our work is to construct a compact functional encryption scheme starting many iO candidates out of which one of them is secure. Let us start with the more ambitious goal of building a robust compact FE combiner. If we have such a combiner, then we achieve our goal since the $i^{th}$ compact FE candidate used in the combiner can be built from the $i^{th}$ iO candidate using prior works [24].

To build a compact FE combiner, we view this problem via the lens of secure multi-party computation: we view every compact FE candidate as corresponding to a party in the MPC protocol; insecure candidates correspond to adversaries. Ananth et al. [1] took the same viewpoint when building an iO combiner and in particular, used non-interactive MPC techniques that relied on DDH/ LWE to solve this problem. Our goal is however to base our combiner only on one-way functions and to achieve that, we start with an interactive MPC protocol.

A first attempt is the following: Let $\varPi _1,\ldots ,\varPi _n$ be the n compact FE candidates. We start with an interactive MPC protocol for parties $P_1,\ldots ,P_n$.

• To encrypt a message x, we secret share x into n additive shares. Each of these shares are encrypted using candidates $\varPi _1,\ldots ,\varPi _n$.

• To generate a functional key for function f, we generate a functional key for the following function $g_i$ using FE candidate $\varPi _i$: this function $g_i$ takes as input message m and executes the next message function of $\varPi _i$ to obtain message $m'$. If $m'$ has to be sent to $\varPi _j$ then it encrypts $m'$ under the public key of $\varPi _j$ and outputs the ciphertext.

The decryption algorithm proceeds as in the evaluation of the multi-party secure computation protocol. Since one of the candidates is secure, say ${\mathbf {i}}^{th}$ candidate, the hope is that the ${\mathbf {i}}^{th}$ ciphertext hides the ${\mathbf {i}}^{th}$ share of x and thus security of FE is guaranteed.

However, implementing the above high level idea faces the following obstacles.

Statelessness: While a party participating in a MPC protocol is stateful, the functional key is not. Hence, the next message function as part of the functional key expects to receive the previous state as input. Its not clear how to ensure without sharing state information with all the other candidates.

Oblivious Transfer: Recall that our goal was to base the combiner only on one-way functions. However, MPC requires oblivious transfer and from Impagliazzo and Rudich’s result [36] we have strong evidence to believe that oblivious transfer cannot be based on one-way functions. Given this, it is unclear how to directly use MPC to achieve our goal.

Randomized Functions: The functional key in the above solution encrypts a message with respect to another candidate. Since encryption is a probabilistic process, we need to devise a mechanism to generate randomness for encrypting the ciphertext.

Correctness Amplification: A recent elegant work of Bitansky and Vaikuntanathan [12] study correctness amplification techniques in the context of indistinguishability obfuscation and functional encryption. Their correctness amplification theorems assume DDH/ LWE to achieve this result. Indeed, this work was also employed by Ananth et al. to construct an iO combiner. We need a different mechanism to handle the correctness issue if our goal is to base our construction on one-way functions.

Tackling Issues: We propose the following ideas to tackle the above issues.

Use 2-ary FE instead of compact FE: The first idea is to replace compact FE candidates with 2-ary FE⁴ candidates. We can build each of 2-ary FE candidates starting from iO candidates. The advantage of using 2-ary FE is two fold:

• 1. It helps in addressing the issue of statelessness. The functional keys, of say $i^{th}$ candidate, are now associated with 2-ary functions, where the first input of the function takes as input the previous state and the other input takes as input the message from another candidate. The output of this function is the updated state encrypted under the public key of the $i^{th}$ candidate and encryption of message under public key of $j^{th}$ candidate, where $j^{th}$ candidate is supposed to receive this message. This way, the state corresponding to the $i^{th}$ candidate is never revealed to any other candidate.

• 2. It also helps in addressing the issue of randomized functions. The first input to the function could also contain a PRF key. This key will be used to generate the randomness required to encrypt messages with respect to public keys of other candidates.

Getting Rid of OT: To deal with this issue, we use the idea of pre-processing OTs that is extensively used in the MPC literature [5, 6, 20, 37]⁵. We pre-compute polynomially many OTs [5] ahead of time. Once we have pre-computed OTs, we can construct an information theoretically secure MPC protocol that is secure upto $n-1$ corruptions, where n is the number of parties. Note that we can only achieve semi-honest security in this setting, achieving malicious security would require that the pre-processing phase outputs exponentially many bits [37].

Next, we consider whether to perform the OT pre-computation as part of the key generation or the encryption algorithm. Depending on where we perform the pre-computation phase, we are faced with the following issues:

• 1. Reusability: In a secure MPC protocol, the pre-computed OTs are used only in one execution of the MPC protocol. So, if we perform the OT pre-computation as part of the key generation algorithm, then the pre-computed OTs need to be reused across different ciphertexts. In this case, no security is guaranteed.

• 2. Compactness: In the current secure MPC with pre-processing solutions, it turns out that the number of OTs to be pre-computed depends on the size of the circuit implementing the MPC functionality. So if we implement the OT pre-computation as part of the encryption algorithm, we need to make sure that the encryption complexity is independent of the number of pre-processed OTs.

We perform the OT pre-computation as part of the encryption algorithm. Hence, we have to deal with the compactness issue stated above. To resolve this, we “compress” the OTs using PRF keys. That is, to generate OTs between two parties $P_i$ and $P_j$, we use a PRF key $K_{ij}$. The next problem is under which public key do we encrypt $K_{ij}$. Encrypting this under either $i^{th}$ candidate or $j^{th}$ candidate could compromise the key completely. The guarantee we want is that as long as one of the two candidates is honest, this key is not compromised. To solve this problem, we employ a 1-out-2 combiner of 2-ary FE – given two candidates, 1-out-2 combiner is secure as long as one of them is secure. This can be achieved by computing an “onion” of two FE candidates. We refer the reader to the technical section for more details.

Correctness Amplification: [12] showed how to transform $\varepsilon$-approximately correct iO into an almost correct iO scheme. They do this in two steps: (i) the first step is the self reducibility step, where they transform approximately correct iO scheme into one, where the iO scheme is correct on every input with probability close to $\varepsilon$, (ii) then they apply BPP amplification techniques to get almost correct iO. Their self reducibility step involves using a type of secure function evaluation scheme and they show how to construct this based on DDH and LWE. We instead show how to achieve the self reducibility step using a single key private key functional encryption scheme. The main idea is as follows: to obfuscate a circuit C, we generate a functional key of C and then obfuscate the FE decryption algorithm with the functional key hardwired inside it. Additionally, we give out the master secret key in the clear along with this obfuscated circuit. To evaluate on an input x, first encrypt this using the master secret key and feed this ciphertext to the obfuscated circuit, which evaluates the decryption algorithm to produce the output. This approach leads to the following issues: (i) firstly, revealing the output of the FE decryption could affect the correctness of iO: for instance, the obfuscated circuit could output $\bot$ for all inputs on which the FE decryption outputs 1, (ii) since the evaluator has the master secret key, he could feed in maliciously generated FE ciphertexts into the obfuscated circuit.

We solve (i) by using by masking the output of the circuit. Here, the mask is supplied as input to the obfuscated circuit. We solve (ii) by using NIZKs with pre-processing, a tool used by Ananth et al. to construct witness encryption combiners. This primitive can be based on one-way functions.

Our Solution in a Nutshell: Summarizing, we take the following approach to build compact FE starting from many iO candidates out of which at least one of them is correct and secure.

• 1. First check if the candidates are approximately correct. If not, discard the candidates.

• 2. Apply the new correctness amplification mechanism on all the remaining iO candidates.

• 3. Construct n 2-ary FE candidates from the n iO candidates obtained from the previous step.

• 4. Then using an onion-based approach, obtain a 2-ary FE combiner that only combines two candidates. This will lead to $N=n^2-n$ candidates.

• 5. Construct a compact FE scheme starting from the above N 2-ary FE candidates and an n-party MPC protocol with OT preprocessing phase. Essentially every $(i,j)^{th}$ 2-ary FE candidate implements a channel between $i^{th}$ and $j^{th}$ party.

We expand on the above high level approach in the relevant technical sections.

3 Preliminaries

Let $\lambda$ be the security parameter. For a distribution $\mathcal {D}$ we denote by $x \xleftarrow {\$}$ an element chosen from $\mathcal {D}$ uniformly at random. We denote that $\big \{\mathcal {D}_{1,\lambda }\big \}\approx _{c,\mu } \big \{\mathcal {D}_{2,\lambda }\big \}$, if for every PPT distinguisher $\mathcal {A}$, $\bigg |\Pr \big [\mathcal {A}(1^{\lambda },x\xleftarrow {\$}\mathcal {D}_{1,\lambda })=1 \big ]- \Pr \big [\mathcal {A}(1^{\lambda },x\xleftarrow {\$}\mathcal {D}_{2,\lambda })=1 \big ] \bigg | \le \mu (\lambda )$ where $\mu$ is a negligible function. For a language L associated with a relation R with denote by $(x,w) \in R$ an instance $x \in L$ with a valid witness w. For an integer $n \in \mathbb {N}$ we denote by [n] the set $\{1,\ldots , n\}$. By $\mathsf {negl}$ we denote a negligible function. We assume that the reader is familiar with the concepts of one-way functions, pseudorandom functions, functional encryption, NIWI, statistically binding commitments and in particular sub-exponential security of these primitives. We say that the one-way function is sub-exponentially secure if no polynomial time adversary inverts a random image with a probability greater than inverse sub-exponential in the length of the input. We refer the reader to full version for the definitions of these primitives.

Important Notation. We introduce some notation that will be useful throughout this work. Consider an algorithm A. We define the time function of A to be T if the runtime of $A(x) \le T(|x|)$. We are only interested in time functions which satisfy the property that $T(\mathrm {poly}(n))=|\mathrm {poly}(T(n))|$. In this section, we describe NIZK with Pre-Processing.

3.1 NIZK with Pre-Processing

We consider a specific type of zero knowledge proof system where the messages exchanged is independent of the input instance till the last round. We call this zero knowledge proof system with pre-processing. The pre-processing algorithm essentially simulates the interaction between the prover and the verifier till the last round and outputs views of the prover and the verifier.

Definition 1

Let L be a language with relation R. A scheme $\mathsf {PZK}=(\mathsf {PZK}.\mathsf {Pre},\mathsf {PZK}.\mathsf {Prove},\mathsf {PZK}.\mathsf {Verify})$ of PPT algorithms is a zero knowledge proof system with pre-processing, $\mathsf {PZK}$, between a verifier and a prover if they satisfy the following properties. Let $(\sigma _V,\sigma _P) \leftarrow \mathsf {PZK}.\mathsf {Pre}(1^\lambda )$ be a preprocessing stage where the prover and the verifier interact. Then:

• 1. Completeness: for every $(x,w) \in R$ we have that:

  $$\begin{aligned} \Pr \left[ \mathsf {PZK}.\mathsf {Verify}(\sigma _V, x, \pi )=1 \ : \ \pi \leftarrow \mathsf {PZK}.\mathsf {Prove}(\sigma _P, x, w)\right] = 1. \end{aligned}$$

  where the probability is over the internal randomness of all the $\mathsf {PZK}$ algorithms.

• 2. Soundness: for every $x \notin L$ we have that:

  $$\begin{aligned} \Pr [\exists \pi : \mathsf {PZK}.\mathsf {Verify}(\sigma _V, x, \pi ) = 1] < 2^{-n} \end{aligned}$$

  where the probability is only over $\mathsf {PZK}.\mathsf {Pre}$.

• 3. Zero-Knowledge: there exists a PPT algorithm S such that for any x, w where $V(x,w)=1$ there exists a negligible function $\mu$ such that it holds that:

  $$\begin{aligned} \{ \sigma _V, \mathsf {PZK}.\mathsf {Prove}(\sigma _P, x, w) \} \approx _{c,\mu } \{ S(x) \} \end{aligned}$$

  We say that $\mathsf {PZK}$ is sub-exponentially secure if $\mu (\lambda )=O(2^{-\lambda ^c})$ for a constant $c>0$.

Such schemes were studied in [21, 40] where they proposed constructions based on one-way functions. Sub-exponentially secure $\mathsf {PZK}$ can be built from sub-exponentially secure one-way functions.

4 Definitions: IO Combiner

We recall the definition of IO combiners from [1]. Suppose we have many indistinguishability obfuscation (IO) schemes, also referred to as IO candidates. We are additionally guaranteed that one of the candidates is secure. No guarantee is placed on the rest of the candidates and they could all be potentially broken. Indistinguishability obfuscation combiners provides a mechanism of combining all these candidates into a single monolithic IO scheme that is secure. We emphasize that the only guarantee we are provided is that one of the candidates is secure and in particular, it is unknown exactly which of the candidates is secure.

We formally define IO combiners next. We start by providing the syntax of an obfuscation scheme. We then present the definitions of an IO candidate and a secure IO candidate. To construct IO combiner, we need to also consider functional encryption candidates. Once we give these definitions, we present our construction in Sect. 5.2.

Syntax of Obfuscation Scheme. An obfuscation scheme associated to a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ with input space $\mathcal {X}_{\lambda }$ and output space $\mathcal {Y}_{\lambda }$ consists of two PPT algorithms $(\mathsf {Obf},\mathsf {Eval})$ defined below.

• Obfuscate, $\overline{C} \leftarrow {\mathsf {Obf}}(1^{\lambda },C)$: It takes as input security parameter $\lambda$, a circuit $C \in \mathcal {C}_{\lambda }$ and outputs an obfuscation of C, $\overline{C}$.

• Evaluation, $y \leftarrow {\mathsf {Eval}}\left( \overline{C},x \right)$: This is usually a deterministic algorithm. But sometimes we will treat it as a randomized algorithm. It takes as input an obfuscation $\overline{C}$, input $x \in \mathcal {X}_{\lambda }$ and outputs $y\in \mathcal {Y}_{\lambda }$.

Throughout this work, we will only be concerned with uniform $\mathsf {Obf}$ algorithms. That is, $\mathsf {Obf}$ and $\mathsf {Eval}$ are represented as Turing machines (or equivalently uniform circuits).

We require that each candidate satisfy the following property called polynomial slowdown.

Definition 2

(Polynomial Slowdown). An obfuscation scheme $\varPi =(\mathsf {Obf},\mathsf {Eval})$ is an IO candidate for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$, with every $C \in \mathcal {C}_{\lambda }$ has size $\mathrm {poly}(\lambda )$, if it satisfies the following property:

Polynomial Slowdown: For every $C \in \mathcal {C}_{\lambda },$ we have the running time of $\mathsf {Obf}$ on input $(1^{\lambda },C)$ to be $\mathrm {poly}(|C|,\lambda )$. Similarly, we have the running time of $\mathsf {Eval}$ on input $(\overline{C},x)$ for $x\in \mathcal {X}_{\lambda }$ is $\mathrm {poly}(|\overline{C}|,\lambda )$.

We now define various notions of correctness.

Definition 3

(Almost/Perfect Correct IO candidate). An obfuscation scheme $\varPi =(\mathsf {Obf},\mathsf {Eval})$ is an almost correct IO candidate for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$, with every $C \in \mathcal {C}_{\lambda }$ has size $\mathrm {poly}(\lambda )$, if it satisfies the following property:

• Almost Correctness: For every $C:\mathcal {X}_{\lambda } \rightarrow \mathcal {Y}_{\lambda }\in \mathcal {C}_{\lambda }, x \in \mathcal {X}_{\lambda }$ it holds that:

  $$\Pr \left[ \forall x \in \mathcal {X}_{\lambda }, \mathsf {Eval}\left( \mathsf {Obf}(1^{\lambda },C),x \right) =C(x) \right] \ge 1-\mathsf {negl},$$

  over the random coins of $\mathsf {Obf}$. The candidate is called a correct IO candidate if this probability is 1.

Definition 4

( $\alpha -$ worst-case Correctness). An obfuscation scheme $\varPi =(\mathsf {Obf},\mathsf {Eval})$ is $\alpha -$worst-case correct IO candidate for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$, with every $C \in \mathcal {C}_{\lambda }$ has size $\mathrm {poly}(\lambda )$, if it satisfies the following property:

• $\alpha -$ worst-case Correctness: For every $C:\mathcal {X}_{\lambda } \rightarrow \{0,1\} \in \mathcal {C}_{\lambda }, x \in \mathcal {X}_{\lambda }$ it holds that:

  $$\Pr \left[ \mathsf {Eval}\left( \mathsf {Obf}(1^{\lambda },C),x \right) =C(x) \right] \ge \alpha ,$$

  over the random coins of $\mathsf {Obf}$ and $\mathsf {Eval}$. The candidate is correct if this probability is 1.

Remark 1

Given any $\alpha -$worst case correct IO candidate where $\alpha >1/2+1/\mathsf {poly}(\lambda )$, as observed by [12] we can gen an almost correct IO candidate while retaining security via BPP amplification.

$\underline{\epsilon -Secure~IO~candidate.}$ If any IO candidate additionally satisfies the following (informal) security property then we define it to be a secure IO candidate: for every pair of circuits $C_0$ and $C_1$ that are equivalent⁶ we have obfuscations of $C_0$ and $C_1$ to be indistinguishable by any PPT adversary.

Definition 5

( $\epsilon$ -Secure IO candidate). An obfuscation scheme $\varPi =(\mathsf {Obf},\mathsf {Eval})$ for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ is a $\epsilon$-secure IO candidate if it satisfies the following conditions:

• Security. For every PPT adversary $\mathcal {A}$, for every sufficiently large $\lambda \in \mathbb {N}$, for every $C_0,C_1 \in \mathcal {C}_{\lambda }$ with $C_0(x)=C_1(x)$ for every $x \in \mathcal {X}_{\lambda }$ and $|C_0|=|C_1|$, we have:

  $$\Big | \Pr \Big [0 \leftarrow {\mathcal {A}}\Big ( \mathsf {Obf}(1^{\lambda },C_0),C_0,C_1 \Big ) \Big ] - \Pr \Big [0 \leftarrow {\mathcal {A}}\Big ( \mathsf {Obf}(1^{\lambda },C_1),C_0,C_1 \Big ) \Big ] \Big | \le \epsilon (\lambda )$$

Remark 2

We say that $\varPi$ is a secure IO candidate if it is a $\epsilon$-secure IO candidate with $\epsilon (\lambda ) = \mathsf {negl}(\lambda )$, for some negligible function $\mathsf {negl}$.

We remarked earlier that the identity function is an IO candidate. However, note that the identity function is not a secure IO candidate. Whenever we refer an IO candidate we will specify the correctness and the security notion it satisfies. For example [4, 24, 33] are examples of $\mathsf {negl}$-secure correct IO candidate. In particular, an IO candidate need not necessarily have any security/correctness property associated with it.

We have the necessary ingredients to define an IO combiner.

4.1 Definition of IO Combiner

We present the formal definition of IO combiner below. First, we provide the syntax of the IO combiner. Later we present the properties associated with an IO combiner.

There are two PPT algorithms associated with an IO combiner, namely, $\mathsf {CombObf}$ and $\mathsf {CombEval}$. Procedure $\mathsf {CombObf}$ takes as input circuit C along with the description of multiple correct IO candidates⁷ and outputs an obfuscation of C. Procedure $\mathsf {CombEval}$ takes as input the obfuscated circuit, input x, the description of the candidates and outputs the evaluation of the obfuscated circuit on input x.

Syntax of IO Combiner. We define an IO combiner $\varPi _{\mathsf {comb}}=(\mathsf {CombObf},\mathsf {CombEval})$ for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$.

• Combiner of Obfuscate algorithms, $\overline{C} \leftarrow {\mathsf {CombObf}}(1^{\lambda },C,\varPi _1,\ldots ,\varPi _n)$: It takes as input security parameter $\lambda$, a circuit $C \in \mathcal {C}$, description of correct IO candidates $\{\varPi _i\}_{i \in [n]}$ and outputs an obfuscated circuit $\overline{C}$.

• Combiner of Evaluation algorithms, $y \leftarrow {\mathsf {CombEval}}(\overline{C},x,\varPi _1,\ldots ,\varPi _n)$: It takes as input obfuscated circuit $\overline{C}$, input x, descriptions of IO candidates $\{\varPi _i\}_{i \in [n]}$ and outputs y.

We define the properties associated to any IO combiner. There are three main properties – correctness, polynomial slowdown, and security. The correctness and the polynomial slowdown properties are defined on the same lines as the corresponding properties of the IO candidates.

The intuitive security notion of IO combiner says the following: suppose one of the candidates is a secure IO candidate then the output of obfuscator ($\mathsf {CombObf}$) of the IO combiner on $C_0$ is computationally indistinguishable from the output of the obfuscator on $C_1$, where $C_0$ and $C_1$ are equivalent circuits.

Definition 6

( $(\epsilon ',\epsilon )$ -secure IO combiner). Consider a circuit class $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$. We say that $\varPi _{\mathsf {comb}}=(\mathsf {CombObf},\mathsf {CombEval})$ is a $(\epsilon ',\epsilon )$ -secure IO combiner if the following conditions are satisfied: Let $\varPi _1,\ldots ,\varPi _n$ be n correct IO candidates for P/poly, and $\epsilon$ is a function of $\epsilon '$.

• Correctness. Let $C \in \mathcal {C}_{\lambda \in \mathbb {N}}$ and $x \in \mathcal {X}_{\lambda }$. Consider the following process: (a) $\overline{C} \leftarrow {\mathsf {CombObf}}(1^{\lambda },C,\varPi _1,\ldots ,\varPi _n)$, (b) $y \leftarrow {\mathsf {CombEval}}(\overline{C},x,\varPi _1,\ldots ,\varPi _n)$.

  Then with overwhelming probability over randomness of $\mathsf {CombObf}$, $\Pr [y=C(x)] \ge 1$, where the probability is over $x\xleftarrow {\$} \mathcal {X}_{\lambda }$.

• Polynomial Slowdown. For every $C:\mathcal {X}_{\lambda } \rightarrow \mathcal {Y}_{\lambda } \in \mathcal {C}_{\lambda },$ we have the running time of $\mathsf {CombObf}$ on input $(1^{\lambda },C,\varPi _1,\ldots ,\varPi _n)$ to be at most $\mathsf {poly}(|C|+n + \lambda )$. Similarly, we have the running time of $\mathsf {CombEval}$ on input $(\overline{C},x,\varPi _1,\ldots ,\varPi _n)$ to be at most $\mathsf {poly}(|\overline{C}|+ n +\lambda )$.

• Security. Let $\varPi _i$ be $\epsilon$-secure correct IO candidate for some $i \in [n]$. For every PPT adversary $\mathcal {A}$, for every sufficiently large $\lambda \in \mathbb {N}$, for every $C_0,C_1 \in \mathcal {C}_{\lambda }$ with $C_0(x)=C_1(x)$ for every $x \in \mathcal {X}_{\lambda }$ and $|C_0|=|C_1|$, we have:

  $$\begin{aligned}&\Big | \Pr \Big [0 \leftarrow {\mathcal {A}}\Big ( \overline{C_0},C_0,C_1,\varPi _1,\ldots ,\varPi _n \Big ) \Big ] - \Pr \Big [0 \leftarrow {\mathcal {A}}\Big ( \overline{C_1},C_0,C_1,\varPi _1,\ldots ,\varPi _n \Big ) \Big ] \Big | \\&\le \epsilon '(\lambda ), \end{aligned}$$

  where $\overline{C_b} \leftarrow {\mathsf {CombObf}}(1^{\lambda },C_b,\varPi _1,\ldots ,\varPi _n)$ for $b \in \{0,1\}$.

Some remarks are in order.

Remark 3

We say that $\varPi _{\mathsf {comb}}$ is an IO combiner if it is a $(\epsilon ',\epsilon )$-secure IO combiner, where, (c) $\epsilon '=\mathsf {negl}'$ and, (d) $\epsilon =\mathsf {negl}$ with $\mathsf {negl}$ and $\mathsf {negl}'$ being negligible functions.

Remark 4

We alternatively call the IO combiner defined in Definition 6 to be a 1-out-n IO combiner. In our construction we make use of 1-out-2 IO combiner. This can be instantiated using a folklore “onion combiner” in which to obfuscate any given circuit one uses both the obfuscation algorithms to obfuscate the circuit one after the other in a nested fashion.

Remark 5

We also define robust combiner, where the syntax is the same as above except that security and correctness properties hold even if there is only one input candidate that is secure and correct. No restriction about correctness and security is placed on other candidates.

As seen in [1], a robust combiner for arbitrary many candidates imply universal obfuscation as defined below.

Definition 7

( $(T,\epsilon )$ -Universal Obfuscation). We say that a pair of Turing machines $\varPi _{\mathsf {univ}}=(\varPi _{\mathsf {univ}}.\mathsf {Obf},\varPi _{\mathsf {univ}}.\mathsf {Eval})$ is a universal obfuscation, parameterized by T and $\epsilon$, if there exists a correct $\epsilon$-secure indistinguishability obfuscator for P/poly with time function T then $\varPi _{\mathsf {univ}}$ is an indistinguishability obfuscator for P/poly with time function $\mathrm {poly}(T)$.

4.2 Definition of 2-ary Functional Encryption Candidate

We now define 2-ary (public-key) functional encryption candidates, also referred to as $\mathsf {MIFE}$ candidates). We start by providing the syntax of a $\mathsf {MIFE}$ scheme.

Syntax of 2-ary Functional Encryption Scheme. A $\mathsf {MIFE}$ scheme associated to a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ consists of four polynomial time algorithms $(\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})$ defined below. Let $\mathcal {X}_{\lambda }$ be the message space of the scheme and $\mathcal {Y}_{\lambda }$ be the space of outputs for the scheme (same as the output space of $\mathcal {C}_{\lambda }$).

• Setup, $(\mathsf {EK}_1,\mathsf {EK}_2,\mathsf {MSK}) \leftarrow {\mathsf {Setup}}(1^{\lambda })$: It is a randomized algorithm takes as input security parameter $\lambda$ and outputs a keys $(\mathsf {EK}_1,\mathsf {EK}_2,\mathsf {MSK})$. Here $\mathsf {EK}_1$ and $\mathsf {EK}_2$ are encryption keys for indices 1 and 2 and $\mathsf {MSK}$ is the master secret key.

• Encryption, $\mathsf {CT}\leftarrow {\mathsf {Enc}}(\mathsf {EK}_i,m)$: It is a randomized algorithm takes the encryption key $\mathsf {EK}_i$ for any index $i\in [2]$ and a message $m\in \mathcal {X}_{\lambda }$ and outputs an encryption of m (encrypted under $\mathsf {EK}_i$).

• Key Generation, $sk_{C} \leftarrow {\mathsf {KeyGen}}\left( \mathsf {MSK}, C\right)$: This is a randomized algorithm that takes as input the master secret key $\mathsf {MSK}$ and a 2-input circuit $C\in \mathcal {C}_{\lambda }$ and outputs a function key $sk_{C}$.

• Decryption, $y \leftarrow {\mathsf {Dec}}\left( sk_C, \mathsf {CT}_1,\mathsf {CT}_2\right)$: This is a deterministic algorithm that takes as input the function secret key $sk_C$ and a ciphertexts $\mathsf {CT}_1$ and $\mathsf {CT}_2$ (encrypted under $\mathsf {EK}_1$ and $\mathsf {EK}_2$ respectively). Then it outputs a value $y\in \mathcal {Y}_{\lambda }$.

Throughout this work, we will only be concerned with uniform algorithms. That is, $(\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})$ are represented as Turing machines (or equivalently uniform circuits).

We define the notion of an $\mathsf {MIFE}$ candidate below. The following definition of multi-input functional encryption scheme incorporates only the correctness and compactness properties of a multi-input functional encryption scheme [31]. In particular, an $\mathsf {MIFE}$ candidate need not necessarily have any security property associated with it. Formally,

Definition 8

(Correct $\mathsf {MIFE}$ candidate). A multi-input functional encryption scheme $\mathsf {MIFE}=(\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})$ is a correct MIFE candidate for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$, with every $C \in \mathcal {C}_{\lambda }$ has size $\mathrm {poly}(\lambda )$, if it satisfies the following properties:

• Correctness: For every $C:\mathcal {X}_{\lambda }\times \mathcal {X}_{\lambda } \rightarrow \{0,1\} \in \mathcal {C}_{\lambda }, m_1,m_2 \in \mathcal {X}_{\lambda }$ it holds that:

  $$ \Pr \left[ \begin{array}{c} (\mathsf {EK}_1,\mathsf {EK}_2,\mathsf {MSK}) \leftarrow {\mathsf {Setup}}(1^{\lambda }) \\ \mathsf {CT}_i \leftarrow {\mathsf {Enc}}(\mathsf {EK}_i,m_i) \textsf { }i\in [2] \\ sk_C \leftarrow {\mathsf {KeyGen}}(\mathsf {MSK},C) \\ C(m_1,m_2) \leftarrow {\mathsf {Dec}}(sk_C,\mathsf {CT}_1,\mathsf {CT}_2) \end{array} \right] \ge 1-\mathsf {negl}(\lambda ),$$

  where $\mathsf {negl}$ is a negligible function and the probability is taken over the coins of the setup only.

• Compactness: Let $(\mathsf {EK}_1,\mathsf {EK}_2,\mathsf {MSK})\leftarrow {\mathsf {Setup}}(1^{\lambda })$, for every $m\in \mathcal {X}_{\lambda }$ and $i\in [2]$, $\mathsf {CT}\leftarrow {\mathsf {Enc}}(\mathsf {EK}_i\,m)$. We require that $|\mathsf {CT}| < poly(|m|,\lambda )$.

A scheme is an MIFE candidate if it only satisfies the correctness and compactness property.

Selective Security. We recall indistinguishability-based selective security for MIFE. This security notion is modeled as a game between a challenger C and an adversary $\mathcal {A}$ where the adversary can request for functional keys and ciphertexts from C. Specifically, $\mathcal {A}$ can submit 2-ary function queries f and respond with the corresponding functional keys. It submits message queries of the form $(m^0_1,m^0_2)$ and $(m^1_1,m^1_2)$ and receive encryptions of messages $m^b_i$ for $i\in [2]$, and for some random bit $b\in \{0,1\}$. The adversary $\mathcal {A}$ wins the game if she can guess b with probability significantly more than 1 / 2 if the following properties are satisfied:

• $f(m^0_1,\cdot )$ is functionally equivalent to $f(m^1_1,\cdot )$.

• $f(\cdot ,m^0_2)$ is functionally equivalent to $f(\cdot , m^1_2)$

• $f(m^0_1,m^0_2)=f(m^1_1,m^1_2)$

Formal definition is presented next.

$\underline{\epsilon -Secure~MIFE~candidate.}$ If any MIFE candidate additionally satisfies the following (informal) security property then we define it to be a secure MIFE candidate:

Definition 9

( $\epsilon$ -Secure MIFE candidate). A scheme $\mathsf {MIFE}$ for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ and message space $\mathcal {X}_{\lambda }$ is a $\epsilon$-secure FE candidate if it satisfies the following conditions:

• ${\mathbf {\mathsf{{MIFE}}}}$ is a correct and compact MIFE candidate with respect to $\mathcal {C}$,

• Security. For every PPT adversary $\mathcal {A}$, for every sufficiently large $\lambda \in \mathbb {N}$, we have:

  $$\Big | \Pr \Big [0 \leftarrow {\mathsf {Expt}}^{\mathsf {MIFE}}_\mathcal {A}\Big ( 1^{\lambda },0 \Big ) \Big ] - \Pr \Big [0 \leftarrow {\mathsf {Expt}}^{\mathsf {MIFE}}_\mathcal {A}\Big (1^{\lambda },1 \Big ) \Big ] \Big | \le \epsilon (\lambda )$$

where the probability is taken over coins of all algorithms. For each $b\in B$ and $\lambda \in \mathbb {N}$, the experiment $\mathsf {Expt}^{\mathsf {MIFE}}_{\mathcal {A}}(1^{\lambda },b)$ is defined below:

• 1. Challenge message queries: $\mathcal {A}$ outputs $(m^0_1,m^0_2)$ and $(m^0_1,m^0_2)$ where each $m^i_j\in \mathcal {X}_{\lambda }$

• 2. The challenger computes $\mathsf {Setup}(1^{\lambda })\rightarrow (\mathsf {EK}_1,\mathsf {EK}_2,\mathsf {MSK})$. It then computes $\mathsf {CT}_1\leftarrow \mathsf {Enc}(\mathsf {EK}_1,m^b_1)$ and $\mathsf {CT}_2\leftarrow \mathsf {Enc}(\mathsf {EK}_1,m^b_2)$. Challenger hands $\mathsf {CT}_1,\mathsf {CT}_2$ to the adversary.

• 3. $\mathcal {A}$ submits functions $f_i$ to the challenger satisfying the constraint given below.

  • $f_i(m^0_1,\cdot )$ is functionally equivalent to $f_i(m^1_1,\cdot )$.

  • $f_i(\cdot ,m^0_2)$ is functionally equivalent to $f_i(\cdot , m^1_2)$

  • $f_i(m^0_1,m^0_2)=f_i(m^1_1,m^1_2)$

  For every i, the adversary gets $sk_{f_i}\leftarrow \mathsf {KeyGen}(\mathsf {MSK},f_i)$.

• 4. Adversary submits the guess $b'$. The output of the game is $b'$.

Remark 6

We say that $\mathsf {MIFE}$ is a secure MIFE candidate if it is a $\epsilon$-secure FE candidate with $\epsilon (\lambda ) = \mathsf {negl}(\lambda )$, for some negligible function $\mathsf {negl}$.

5 Construction of IO Combiner

In this section we describe our construction for IO combiner. We first define an MPC framework that will be used in our construction.

5.1 MPC Framework

We consider an MPC framework in the pre-processing model described below. Intuitively the input is pre-processed and split amongst n deterministic parties which are also given some correlated randomness. Then, they run a protocol together to compute f(x) for any function f of the input x. The syntax consists of the following algorithms:

• $\mathsf {Preproc}(1^\lambda ,n,x)\rightarrow (x_1,\mathsf {corr}_1,..,x_n,\mathsf {corr}_n)$: This algorithm takes as input $x\in \mathcal {X}_{\lambda }$, the number of parties computing the protocol n, and the security parameter $\lambda$. It outputs strings $x_i,\mathsf {corr}_i$ for $i\in [n]$. Each $\mathsf {corr}_i=\mathsf {corr}_i(r)$ is represented both a function and a value depending on the context. $(x_1,..,x_n)$ forms a secret sharing of x.

• $\mathsf {Eval}(\mathsf {Party}_1(x_1,\mathsf {corr}_1),..,\mathsf {Party}_n(x_n,\mathsf {corr}_n),f)\rightarrow f(x)$: The evaluate algorithm is a protocol run by n parties with $\mathsf {Party}_i$ having input $x_i,\mathsf {corr}_i$. Each $\mathsf {Party}_i$ is deterministic. The algorithm also takes as input the function $f\in \mathcal {C}_{\lambda }$ of size bounded by $\mathsf {poly}(\lambda )$ and it outputs f(x).

We now list the notations used for the protocol.

• 1. The number of rounds in the protocol is given by a polynomial $t_{f}(\lambda ,n,|x|)$.

• 2. For every $i\in [n]$, $\mathsf {corr}_i=\{\mathsf {corr}_{i,j}\}_{j\ne i}$. Let $len_{f}=len_{f}(\lambda ,n)$ denote a polynomial. Then, for each $i,j\in [n]$ such that $i\ne j$, $\mathsf {corr}_{i,j}$ and $\mathsf {corr}_{j,i}$ are generated as follows. Sample $r_{i,j}\xleftarrow {\$} \{0,1\}^{len_f}$ then compute $\mathsf {corr}_{i,j}=\mathsf {corr}_{i,j}(r_{i,j})$ and $\mathsf {corr}_{j,i}=\mathsf {corr}_{j,i}(r_{i,j})$.

• 3. There exists an efficiently computable function $\phi _f$ that takes as input a round number $k\in [t_f]$ and outputs $\phi _f(k)=(i,j)$. Here, (i, j) represents that the sender of the message at $k^{th}$ round is $\mathsf {Party}_i$ and the recipient is $\mathsf {Party}_j$.

• 4. The efficiently computable next message function for every round $k\in [t_f]$, $M_k$ does the following. Let $\phi _f(k)=(i,j)$. Then, $M_k$ takes as input $(x_i,y_1,..,y_{k-1},\mathsf {corr}_{i,j})$ and outputs the next message as $y_k$.

Correctness: We require the following correctness property to be satisfied by the protocol. For every $n,\lambda \in \mathbb {N}$, $x\in \mathcal {X}_{\lambda }$, $f\in \mathcal {C}_{\lambda }$ it holds that:

$$ Pr \left[ \begin{array}{c} (x_1,\mathsf {corr}_1,..,x_n,\mathsf {corr}_n) \leftarrow {\mathsf {Preproc}}(1^{\lambda },n,x) \\ \mathsf {Eval}(\mathsf {Party}_1(x_1,\mathsf {corr}_1),...,\mathsf {Party}_n(x_n,\mathsf {corr}_n),f) \rightarrow f(x) \end{array} \right] =1,$$

Here the probability is taken over coins of the algorithm $\mathsf {Preproc}$.

Security Requirement. We require the security against static corruption of $n-1$ semi-honest parties. Informally the security requirement is the following. There exists a polynomial time algorithm that takes as input f(x) and inputs of $n-1$ corrupt parties $\{ (\mathsf {corr}_i,x_i) \}_{i\ne i^{*}}$ and simulates the outgoing messages of $\mathsf {Party}_{i^{*}}$. Formally, consider a PPT adversary $\mathcal {A}$. Let the associated PPT simulator be Sim. We define the security experiment below.

$\underline{\mathsf {Expt}_{real,\mathcal {A}}(1^{\lambda })}$

• $\mathcal {A}$ on input $1^{\lambda }$ outputs n, the circuit f and input x along with the index of the honest party, $i^{*} \in [n]$.

• Secret share x into $(x_1,..,x_n)$.

• Part of the pre-processing step is performed by the adversary. For every $i>j$ such that $i^* \ne i$ and $i^* \ne j$, $\mathcal {A}$ samples $r_{i,j}\xleftarrow {\$} \{0,1\}^{len_f}$. Then, it computes, $\mathsf {corr}_{i,j}=\mathsf {corr}_{i,j}(r_{i,j})$ and $\mathsf {corr}_{j,i}=\mathsf {corr}_{j,i}(r_{i,j})$.

• Sample $r_{j}\xleftarrow {\$} \{0,1\}^{len_f}$ for $j\ne i^{*}$. Then compute $\mathsf {corr}_{i^{*},j}=\mathsf {corr}_{i^{*},j}(r_j)$ and $\mathsf {corr}_{j,i^{*}}=\mathsf {corr}_{j,i^{*}}(r_j)$. We denote $\mathsf {corr}_i=\{\mathsf {corr}_{i,j}\}_{j \ne i}$. This completes the pre-processing step.

• Let $y_1,..,y_{t_f}$ be the messages computed by the parties in the protocol computing f(x). Output $\big (\{x_i,\mathsf {corr}_i\}_{i\ne i^{*}},y_1,..,y_{t_f} \big )$. In MPC literature $(\{x_i,\mathsf {corr}_i\}_{i\ne i^{*}},y_1,..,y_{t_f})$ is referred to the view of the adversary in this experiment. We refer this as $\mathsf {view}_{\mathsf {Expt}_{real,\mathcal {A}}}$.

$\underline{\mathsf {Expt}_{ideal,\mathcal {A}}(1^{\lambda })}$

• $\mathcal {A}$ on input $1^{\lambda }$ outputs n, the circuit f and input x along with the index of the honest party, $i^{*} \in [n]$.

• Secret share x into $(x_1,..,x_n)$.

• Part of the pre-processing step is performed by the adversary. For every $i>j$ such that $i^* \ne i$ and $i^* \ne j$, $\mathcal {A}$ samples $r_{i,j}\xleftarrow {\$} \{0,1\}^{len_f}$. Then, it computes, $\mathsf {corr}_{i,j}=\mathsf {corr}_{i,j}(r_{i,j})$ and $\mathsf {corr}_{j,i}=\mathsf {corr}_{j,i}(r_{i,j})$.

• Sample $r_{j}\xleftarrow {\$} \{0,1\}^{len_f}$ for $j\ne i^{*}$. Then compute $\mathsf {corr}_{i^{*},j}=\mathsf {corr}_{i^{*},j}(r_j)$ and $\mathsf {corr}_{j,i^{*}}=\mathsf {corr}_{j,i^{*}}(r_j)$. This completes the pre-processing step.

• Compute $Sim \big (1^{\lambda },1^{|f|},f(x),\{x_i,\mathsf {corr}_i\}_{i\ne i^{*}} \big )$. Output the result. We refer this as $\mathsf {view}_{\mathsf {Expt}_{ideal,\mathcal {A}}}$.

We require that the output of both the above experiments is computationally indistinguishable from each other. That is,

Definition 10

(Security). Consider a PPT adversary $\mathcal {A}$ and let the associated PPT simulator be Sim. For every PPT distinguisher $\mathcal {D}$, for sufficiently large security parameter $\lambda$, it holds that:

$$\left| \Pr \left[ 1 \leftarrow {\mathcal {D}}\left( \mathsf {Expt}_{real,\mathcal {A}}(1^{\lambda }) \right) \right] - \Pr \left[ 1 \leftarrow {\mathcal {D}}(\mathsf {Expt}_{ideal,\mathcal {A}}\left( 1^{\lambda }) \right) \right] \right| \le \mathsf {negl}(\lambda ),$$

where $\mathsf {negl}$ is some negligible function.

Instantiation of MPC Framework: We show how to instantiate this MPC framework. We use a 1-out-of-n (i.e., $n-1$ of them are insecure) information theoretically secure MPC protocol secure against passive adversaries [30, 38] in the OT hybrid model. We then replace the OT oracle by preprocessing all the OTs [5] before the execution of the protocol begins. Note that every OT pair is associated exactly with a pair of parties.

5.2 Construction Roadmap

In this section, we describe the roadmap of our construction. We start with n IO candidates, $\varPi _1,..,\varPi _n$ and construct $n^2-n$ IO candidates $\varPi _{i,j}$ where $i\ne j$. $\varPi _{i,j}$ is constructed by using an onion obfuscation combiner (one in which each obfuscation candidate is run sequentially on the circuit). Each candidate $\varPi _{i,j}$ is now used to construct a 2-ary public-key multi-input functional encryption scheme $\mathsf {FE}_{i,j}$ candidates using [9, 31] (this step uses the existence of one-way function). This is because [31] uses an existence of a public-key encryption, statistically binding commitments and statistically sound non-interactive witness-indistinguishable proofs. All these primitives can be constructed using IO and one-way functions as shown in works such as [9, 46]. These primitives maintain binding/soundness as long as the underlying candidate is correct.

Any candidate $\mathsf {FE}_{i,j}$ is secure as long as either $\varPi _i$ or $\varPi _j$ is secure. This follows from the security of onion obfuscation combiner. We describe below how to construct a compact functional encryption $\mathsf {FE}$ from these multi-input functional encryption candidates and MPC framework in Sect. 5.3. Finally, using [2, 11] and relying on complexity leveraging we construct a secure IO candidate $\varPi _{comb}$ from $\mathsf {FE}$. Below is a flowchart describing the roadmap.

5.3 Constructing Compact FE from $n^2-n$ $\mathsf {FE}$ Candidates

Consider the circuit class $\mathcal {C}$. We now present our construction for a compact functional encryption scheme $\mathsf {FE}$ for $\mathcal {C}$ starting from compact multi-input functional encryption candidates $\mathsf {FE}_{i,j}$ for $\mathcal {C}$. Let $\varGamma$ be a secure MPC protocol described in Sect. 5.1. Let $\lambda$ be the security parameter and F denote a pseudorandom function (PRF) where $F:\{0,1\}^{\lambda }\times \{0,1\}^*\rightarrow \{0,1\}^{len(\lambda )}$ where len is some large enough polynomial. Finally let $\mathsf {Com}$ be a statistically binding commitment scheme.

$\underline{\mathsf {FE}.\mathsf {Setup}(1^{\lambda })}$ Informally, the setup algorithm samples encryption and master secret keys for candidates $\mathsf {FE}_{i,j}$ such that $i\ne j$ and $i,j\in [n]$. These candidates act as a channel between candidate i and j. It also samples $\mathsf {NIWI}_{i,j}$ prover strings for these candidates to prove consistency of the messages computed during the protocol.

• 1. Setting up MIFE candidates:

  • For every $i,j\in [n]$ and $i\ne j$ run $\mathsf {FE}_{i,j}.\mathsf {Setup}(1^\lambda ) \rightarrow (\mathsf {EK}_{i,j,1},\mathsf {EK}_{i,j,2},$ $\mathsf {MSK}_{i,j})$

• 2. Sample NIWI prover strings

  • Run $\mathsf {NIWI}_{i,j}.\mathsf {Setup}\rightarrow \sigma _{i,j}$ for $i,j\in [n]$ and $i\ne j$. Recall, $\mathsf {NIWI}_{i,j}$ is a non-interactive statistically sound witness-indistinguishable proof scheme (in the CRS model) constructed using IO candidate $\varPi _{i,j}$ and any one-way function as done in [9]⁸. This proof scheme remains sound if the underlying obfuscation candidate is correct/almost correct. The proof retains witness indistinguishability if the candidate is additionally secure.

  • Output $\mathsf {MPK}=\{\mathsf {EK}_{i,j,1}, \mathsf {EK}_{i,j,2},\sigma _{i,j}\}_{i,j\in [n], i\ne j}$ and $\mathsf {MSK}=\{\mathsf {MSK}\}_{i,j\in [n], i\ne j}$.

$\underline{\mathsf {FE}.\mathsf {Enc}(\mathsf {MPK},m)}$. Informally, the encryption algorithm takes the message m and runs preprocessing to get $(m_1,\mathsf {corr}'_1,...,m_n,\mathsf {corr}'_n)$. It discards $\mathsf {corr}'_i$ (which is allowed by our MPC framework). Then it samples PRF keys $K_{i,j}$ for $i\ne j$, which are used to generate randomness for next message function (via computing $\mathsf {corr}_i$ for every decryption). It also commits these message shares $m_i$ and PRF keys, which are used to compute proofs about messages of the MPC protocol. Finally, these shares and PRF keys are encrypted using an appropriate $\mathsf {FE}$ candidate.

• 1. MPC Preprocessing

  • Run $\mathsf {Preproc}(1^{\lambda },n,m) \rightarrow (m_1,\mathsf {corr}'_1,..,m_n,\mathsf {corr}'_n)$. Compute commitments $Z_{\mathsf {in},i}=\mathsf {Com}(m_i)$ for all $i\in [n]$. Let $r_{\mathsf {in}, i}$ be the corresponding randomness.

• 2. Sample and commit PRF keys

  • Sample PRF keys $K_{i,j}$ for $i,j\in [n]$ and $i\ne j$ with the constraint that $K_{i,j}=K_{j,i}$. Compute $Z_{i,j}=\mathsf {Com}(K_{i,j})$ for $i,j\in [n]$ and $i\ne j$. Let $r_{i,j}$ be the corresponding randomness.

  • Sample PRF keys $K^{'}_{i,j}$ for $i,j\in [n]$ such that $i\ne j$.

• 3. Compute encryptions

  • For every $i,j\in [n]$ and $i\ne j$ compute $\mathsf {CT}_{i,j}=\mathsf {FE}_{i,j}.\mathsf {Enc}(\mathsf {EK}_{i,j,1},m_i,$ $K_{i,j},K^{'}_{i,j},\{Z_{\mathsf {in},k},Z_{k,j}\}_{k,j\in [n],k\ne j},r_{i,j},r_{\mathsf {in},i}, \bot )$. Here $\bot$ is a slot of size $\mathsf {poly}(\lambda )$, which is described later.

  • Output $\mathsf {CT}=\{\mathsf {CT}_{i,j} \}_{i\ne j}$

$\underline{\mathsf {FE}.\mathsf {KeyGen}(\mathsf {MSK},C)}$. Let $t_{C}$ denote the number of rounds for the MPC protocol $\varGamma$ for computing the circuit C. Let $len_{msg}$ denote the maximum length of any message sent in the protocol while computing C on input. Informally, this algorithm generates $\mathsf {FE}$ keys for the circuits implementing next message function (used to compute C(m)) for every round $k\in [t_C]$.

• 1. Computing commitments

  • Compute $Z_{\mathsf {out},i}\leftarrow \mathsf {Com}(\bot ^{len_{msg}})$ for $i \in [t_{C}]$.

• 2. Compute secret-key encryptions

  • Let $\mathsf {E}$ by a secret-key encryption scheme. Run $\mathsf {E}.\mathsf {Setup}(1^{\lambda })\rightarrow sk$. For every $i\in [t_{C}]$, compute $c_i=\mathsf {E}.\mathsf {Enc}(sk,0)$. These encryptions encrypt messages of sufficient length (described later).

• 3. Generate keys

  • Sample a random $\mathsf {tag}\in \{0,1\}^{\lambda }$.

  • For every round $k\in [t_C]$, let $\phi (k)=(i',j')$, generate a key $sk_{C,k}\leftarrow \mathsf {FE}_{i',j'}.\mathsf {KeyGen}(\mathsf {MSK}_{i',j'},G_k)$ where $G_k$ is described in Fig. 1. Output $\{sk_{C,k}\}_{k\in [t_C]}$.

Fig. 1.

Circuit $G_k$

$\underline{\mathsf {FE}.\mathsf {Dec}(sk_C,\mathsf {CT})}$w

• 1. Evaluating the MPC protocol for circuit C

  • Let $\phi (1)=(i_1,j_1)$. Compute $\mathsf {CT}_{1}=\mathsf {FE}_{i_1,j_1}.\mathsf {Enc}(\mathsf {EK}_{i_1,j_1,2},\bot ,\bot )$.

    Set $(x_1,\pi _1)=\mathsf {FE}_{i,j}.\mathsf {Dec}(sk_{C,1},\mathsf {CT}_{i_1,j_1},\mathsf {CT}_{1})$.

  • For every round $k\in [t_C]$, compute $x_k,\pi _k$ iteratively from $x_1,\pi _1,$ $..,x_{k-1},\pi _{k-1}$ as described below.

    • a Compute $\phi (k)=(i,j)$. Then, compute $\mathsf {CT}_{k}=\mathsf {FE}_{i,j}.\mathsf {Enc}(\mathsf {EK}_{i,j,2},$ $x_{1},\pi _1,..,x_{k-1},\pi _{k-1})$.

    • b Run $(x_k,\pi _k)\leftarrow \mathsf {FE}_{i,j}.\mathsf {Dec}(sk_{C,k},\mathsf {CT}_{i,j},\mathsf {CT}_{k})$

  • Output $x_{t_C}$

Correctness: If the underlying MPC protocol is correct and the multi-input functional encryption candidates $\mathsf {FE}_{i,j}$ are correct then one can inspect that our scheme satisfies correctness.

Compactness. Compactness is discussed next. The cipher-text encrypting any message m, consists of $\mathsf {FE}_{i,j}$ encryptions $\mathsf {CT}_{i,j}$ for any $i,j\in [n]$ such that $i\ne j$. Each $\mathsf {CT}_{i,j}$ encrypts $m_i,K_{i,j},K^{'}_{i,j},\{Z_{\mathsf {in},k},Z_{k,j}\}_{k,j\in [n],k\ne j}, r_{i,j},r_{\mathsf {in},i},\bot$. Note that $m_i$ is of the same length of the message where as $K_{i,j},K^{'}_{i,j}$ are just the PRF keys that are of length $\lambda$. $\{Z_{\mathsf {in},k},Z_{k,j}\}_{k,j\in [n],k\ne j}$ are commitments of $m_i$ and the PRF keys respectively while $r_{i,j}$ and $r_{\mathsf {in},i}$ is the randomness used for the commitments $Z_{i,j}$ and $Z_{\mathsf {in},i}$. $\bot$ is a slot of size $\mathsf {poly}(\lambda )$ (which is the length of the decryption key for scheme $\mathsf {E}$). All these strings are of a fixed polynomial size (polynomial in $n,\lambda , |m|$). If the underlying scheme $\mathsf {FE}_{i,j}$ is compact, the scheme $\mathsf {FE}$ is also compact. We give a brief sketch of proof here. We refer the reader to our full version for a detailed proof.

Theorem 4

Consider the circuit class $\mathcal {C}= P/poly$. Assuming $\varGamma$ is a secure MPC protocol for $\mathcal {C}$ according to the framework described in Sect. 5.1 and one-way functions exist, then scheme $\mathsf {FE}$ is a secure functional encryption scheme as long as there is $i^{*}\in [n]$ such that $\varPi _{i^*}$ is a secure candidate.

Proof

(Sketch). We now sketch the security proof of this theorem. Assume $\varPi _{i^*}$ is a secure IO candidate. This implies $\mathsf {FE}_{i^*,j}$ and $\mathsf {FE}_{j,i^*}$ is secure for any $j\ne i^*$. We use this crucially in our proofs. We employ the standard hybrid argument to prove the theorem. In the first hybrid ($\mathsf {Hyb}_1$), the message $M_b$ is encrypted honestly with $b \xleftarrow {\$} \{0,1\}$. In the final hybrid ($\mathsf {Hyb}_9$), the ciphertext contains no information about b. At this point, the probability of guessing the bit b is exactly 1 / 2. By arguing indistinguishability of every consecutive intermediate hybrids, we show that the probability of guessing b in the first hybrid is negligibly close to 1 / 2 (or the advantage is 0), which proves the theorem.

The first hybrid corresponds to the regular FE security game. Then we switch to a hybrid where the secret-key encryption cipher-text $c_i$ in the function keys for all rounds $i\in [t_C]$ are hard-wired as encryptions of the output of the MIFE decryption in those rounds. This can be done, because the cipher-text and the function key fixes these outputs (as a function of PRF keys, e.t.c). Then, we change the commitments $Z_{\mathsf {out},k}$ to commtiments of message output in round k (for k such that the $i^{*}$ is the receiving or sending party in that round). This security holds due to the security of the commitment. In the next hybrid, we rely on the security of the scheme $\mathsf {FE}_{i^{*},j}$ and $\mathsf {FE}_{j,i^{*}}$ by generating encryptions that does not contain the PRF keys and the openings of the commitments but only contain the secret key for the encryption scheme $\mathsf {E}$. Now we invoke the security of the PRF to generate proofs $\pi _k$ hard-wired in $c_k$ for any round k (for k such that the $i^{*}$ is the receiving or sending party in that round) randomly. Next, we rely on the security of $\mathsf {NIWI}_{i^{*},j}$ and $\mathsf {NIWI}_{j,i^{*}}$ to use the opening of $Z_{\mathsf {out},k}$ (for k such that the $i^{*}$ is the receiving or sending party in that round) to generate the proofs. Now relying on the security of commitment scheme, we make the commitments $Z_{i^{*},j},Z_{j,i^{*}}$ and $Z_{\mathsf {in},i^{*}}$ to commit to $\bot$. Then we use the security of the PRF to generate $\mathsf {corr}_{i^{*},j}$ and $\mathsf {corr}_{j,i^{*}}$ (used for generating outputs $x_n$) randomly. Finally, we invoke the security of the MPC framework (by using the simulator) to make the game independent of b.

5.4 Summing Up: Combiner Construction

We now give the combiner construction:

• $\mathsf {CombObf}(1^{\lambda },C,\varPi _1,..,\varPi _n):$ Use $\varPi _1,..,\varPi _n$ and any one-way function to construct a compact functional encryption $\mathsf {FE}$ as in Sect. 5.2. Use [2, 11] to construct an obfuscator $\varPi _{comb}$. Output $\overline{C}\leftarrow {\varPi }_{comb}(1^{\lambda },C)$.

• $\mathsf {CombEval}(\overline{C},x):$ Output $\varPi _{comb}.\mathsf {Eval}(\overline{C},x)$.

Correctness of the scheme is straight-forward to see because of the correctness of $\mathsf {FE}$ as shown in Sect. 5.2. The security follows from the sub-exponential security of construction in Sect. 5.2. The construction in Sect. 5.2 is sub-exponentially secure as long as the underlying primitives are sub-exponentially secure.

We now state the theorem.

Theorem 5

Assuming sub-exponentially secure one-way functions, the construction described above is a $(\mathsf {negl},2^{-\lambda ^{c}})-$secure IO combiner for P / poly where $c>0$ is a constant and $\mathsf {negl}$ is some negligible function.

6 From Combiner to Robust Combiner

The combiner described in Sect. 5.2, is not robust. It guarantees no security/correctness if the underlying candidates are not correct. A robust combiner provides security/correctness as long as there exists one candidate $\varPi _{i^*}$ such that it is secure and correct. There is no other restriction placed on the other set of candidates. A robust combiner for arbitrary many candidates imply universal obfuscation [1].

In this section we describe how to construct a robust combiner. The idea is the following.

• We correct the candidates (upto overwhelming probability) before feeding it as input to the combiner.

• First, we leverage the fact that secure candidate is correct. We transform each candidate so that all candidates are $(1-1/\lambda )-$worst case correct while maintaining security of the secure candidate.

• Then using [12] we convert a worst-case correct candidate to an almost correct candidate.

In the discussion below, we assume $\mathcal {C}$ consists polynomial size circuits with one bit output. One can construct obfuscator for circuits with multiple output bits from obfuscator with one output bit. For simplicity let us assume that $\mathcal {C}_{\lambda }$ consists of circuits with input length $p(\lambda )$ for some polynomial p.

6.1 Generalised Secure Function Evaluation

The starting point to get a worst-case correct IO candidate is a variant of “Secure Function Evaluation” (SFE) scheme as considered in [12]. They use SFE to achieve worst-case correctness by obfuscating evaluation function of SFE for the desired circuit C. To evaluate on input x, the evaluator first encodes x according to the SFE scheme and feeds it as an input to the obfuscated program. Then, it finally decodes the result as the output of the obfuscated program. Worst case correctness is guaranteed because using the information hard-wired in the obfuscated program its hard to distinguish an encoding of any input $x_1$ from that of $x_2$.

We essentially use the same idea except that we consider a variant of SFE with a setup algorithm (which produces secret parameters), and the evaluation function for the circuit C is not public. It requires some helper information to perform evaluation on the input encodings.

We consider a generalised variant of secure function evaluation [12] with the following properties. Let $\mathcal {C}_{\lambda }$ be the allowed set of circuits. Let $\mathcal {X}_{\lambda }$ and $\mathcal {Y}_{\lambda }$ denote the ensemble of inputs and outputs. A secure function evaluation scheme consists of the following algorithms:

• $\mathsf {Setup}(1^{\lambda }):$ On Input $1^{\lambda }$, the setup algorithm outputs secret parameters $\mathsf {SP}$.

• $\mathsf {CEncode}(\mathsf {SP},C):$ The randomized circuit encoding algorithm on input a circuit $C\in \mathcal {C}_{\lambda }$ and $\mathsf {SP}$ outputs another $\tilde{C}\in \mathcal {C}_{\lambda }$.

• $\mathsf {InpEncode}(\mathsf {SP},x):$ The randomized input encoding algorithm on input $x\in \mathcal {X}_{\lambda }$ and $\mathsf {SP}$ outputs $(\tilde{x},z) \in \mathcal {X}_{\lambda } \times \mathcal {Z}_{\lambda }$.

• $\mathsf {Decode}(y,z):$ Let $y=\tilde{C}(\tilde{x})$. The deterministic decoding algorithm takes as input y and z to recover $C(x)\in \mathcal {Y}_{\lambda }$.

We require the following properties:

Input Secrecy: For any $x_1,x_2 \in \mathcal {X}_{\lambda }$, any circuit $C\in \mathcal {C}_{\lambda }$ and $\mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda })$, it holds that:

$$\{ \mathsf {CEncode}(\mathsf {SP},C),\mathsf {InpEncode}(\mathsf {SP},x_1) \} \approx _c$$

$$\{ \mathsf {CEncode}(\mathsf {SP},C),\mathsf {InpEncode}(\mathsf {SP},x_2) \}$$

Correctness: For any circuit $C\in \mathcal {C}_{\lambda }$ and any input x, it holds that:

$$Pr[ \mathsf {Decode}(\tilde{C}(\tilde{x}),z )=C(x) ] =1$$

where $\mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda }), \tilde{C}\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C), (\tilde{x},z)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x)$ and the probability is taken over coins of all the algorithms.

Functionality: For any equivalent circuits $C_0,C_1$, $\mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda })$, $\tilde{C}_0\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C_0)$ and $\tilde{C}_1\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C_1)$, it holds that $\tilde{C}_0$ is equivalent to $\tilde{C}_1$ with overwhelming probability over the coins of setup and the circuit encoding algorithm. This captures the behaviour of the circuit encodings when evaluated on maliciously generated input encodings.

6.2 Modified Obfuscation Candidate

In this section we achieve the following. Given any candidate $\varPi$, we transform it to a candidate $\varPi '$ such that the following holds:

• If $\varPi$ is both secure and correct, then so is $\varPi '$.

• Otherwise $\varPi '$ is guaranteed to be $(1-1/\lambda )-$worst-case correct.

In either case, we can amplify its correctness to get an almost correct IO candidate, which can be used by our combiner construction. Given any IO candidate $\varPi$ we now describe a modified IO candidate $\varPi '$. For simplicity let us assume that $\mathcal {C}_{\lambda }$ consists of circuits with one bit output and input space $\mathcal {X}_{\lambda }$ corresponds to the set $\{0,1\}^{p(\lambda )}$ for some polynomial p. Let $\mathsf {SFE}$ be a secure function evaluation scheme as described in Sect. 6.1 for $\mathcal {C}_{\lambda }$ with $\mathcal {Z}_{\lambda }=\mathcal {Y}_{\lambda }=\{0,1\}$.

• Obfuscate: On input the security parameter $1^{\lambda }$ and $C\in \mathcal {C}_{\lambda }$, first run $\mathsf {SP}\leftarrow {\mathsf {SFE}}.\mathsf {Setup}(1^{\lambda })$, compute $\tilde{C} \leftarrow \mathsf {CEncode}(\mathsf {SP},C)$. We now define an algorithm $\mathsf {Obf}_{int,\varPi }$ that takes as input $\tilde{C}$ and $1^{\lambda }$ and does the following:

  • - Compute $\overline{C}\leftarrow {\varPi }.\mathsf {Obf}(1^{\lambda },\tilde{C})$.

  • - Then sample randomly $x_1,..,x_{\lambda ^2}\in \{0,1\}^{p(\lambda )}$. Compute $(\tilde{x}_i,z_i)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x_i)$. Check that $\varPi .\mathsf {Eval}(\overline{C},\tilde{x}_i)=\tilde{C}(\tilde{x}_i)$ for all $i\in [\lambda ^2]$.

  • - If the check passes output $\overline{C}$, otherwise output $\tilde{C}$ ⁹.

  Output of the obfuscate algorithm is $(\mathsf {SP},\mathsf {Obf}_{int,\varPi }(\tilde{C}) )$.

• Evaluate: On input $(\mathsf {SP},\overline{C})$ and an input x, first compute $(\tilde{x},z)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x)$. Then compute $\tilde{y} \leftarrow {\varPi }.\mathsf {Eval}(\overline{C} , \tilde{x})$ or $\tilde{y} \leftarrow \overline{C} (\tilde{x} )$ depending on the case if $\overline{C}=\tilde{C}$ or not. We define as an intermediate evaluate algorithm, i.e. $\tilde{y}=\mathsf {Eval}_{int,\varPi }(\overline{C},\tilde{x})$.

  Output $y=\mathsf {SFE}.\mathsf {Decode}(\tilde{y},z )$.

Few claims are in order:

Theorem 6

Assuming $\mathsf {SFE}$ is a secure function evaluation scheme as described in Sect. 6.1, if $\varPi$ is a secure and correct candidate, then so is, $\varPi '$.

Proof

We deal with this one by one. First we argue security. Note that when $\varPi$ is correct, the check at $\lambda ^2$ random points passes. In this case the obfuscation algorithm always outputs $(\mathsf {SP},\varPi .\mathsf {Obf}(1^{\lambda },\tilde{C}_b))$ where $\tilde{C}_b\leftarrow {\mathsf {SFE}}.\mathsf {CEncode}(\mathsf {SP},C_b)$ for $b\in \{0,1\}$ and $\mathsf {SP}\leftarrow {\mathsf {SFE}}.\mathsf {Setup}(1^{\lambda })$. Since, $\tilde{C}_0$ is equivalent to $\tilde{C}_1$ due to functionality property of the SFE scheme, the security holds due to the security of $\varPi$.

The correctness holds due to the correctness of SFE and $\varPi$.

Theorem 7

Assuming $\mathsf {SFE}$ is a secure function evaluation scheme as described in Sect. 6.1, if $\varPi$ is an IO candidate, then $\varPi '$ is $(1-2/\lambda )$-worst case correct IO candidate.

Proof

The check step in the obfuscate algorithm ensures the following: Using Chernoff bound it follows that, with overwhelming probability, for any circuit C,

$$\begin{aligned} Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x)=C(x) | (\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C), x\xleftarrow {\$} \mathcal {U}_{p(\lambda )} ] \ge (1-1/\lambda ) \end{aligned}$$

(1)

We now prove that for any $x_1,x_2$ it holds that, with overwhelming probability over coins of obfuscate algorithm, for any circuit C,

$$\begin{aligned} \begin{aligned} | Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x_1)=C(x_1) |&(\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C)] -\\ Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x_2)=C(x_2) |&(\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C)] | \le \mathsf {negl}(\lambda ) \end{aligned} \end{aligned}$$

(2)

This is because for any input x,

$$\begin{aligned} \begin{aligned} Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x)=C(x) |&(\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C)]=\\Pr[\mathsf {Eval}_{int,\varPi }(\overline{C},\tilde{x}) = \tilde{C}(\tilde{x}) |&\mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda }), \tilde{C}\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C), \\(\tilde{x},z)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x),&\overline{C}\leftarrow {\mathsf {Obf}}_{int,\varPi }(1^{\lambda },\tilde{C})] \end{aligned} \end{aligned}$$

(3)

Note that due to the input secrecy property of the SFE scheme we have that,

$$\begin{aligned} \begin{aligned} | Pr[\mathsf {Eval}_{int,\varPi }(\overline{C},\tilde{x}_1) = \tilde{C}(\tilde{x_1}) | \mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda }), \tilde{C}\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C), \\(\tilde{x_{1}},z_1)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x_1), \overline{C}\leftarrow {\mathsf {Obf}}_{int,\varPi }(1^{\lambda },\tilde{C})]-\\Pr[\mathsf {Eval}_{int,\varPi }(\overline{C},\tilde{x}_2) = \tilde{C}(\tilde{x_2}) | \mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda }), \tilde{C}\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C), \\(\tilde{x_{2}},z_2)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x_2), \overline{C}\leftarrow {\mathsf {Obf}}_{int,\varPi }(1^{\lambda },\tilde{C})]|<\mathsf {negl}(\lambda ) \end{aligned} \end{aligned}$$

(4)

for a negligible function $\mathsf {negl}$. Otherwise we can build a reduction $\mathcal {R}$ that given any circuit-encoding, input encoding pair $\tilde{C},\tilde{x}_b$ decides if $b=0$ or $b=1$ with a non-negligible probability. The reduction just computes $\overline{C}\leftarrow {\mathsf {Obf}}_{int,\varPi }(\tilde{C})$ and checks if $\mathsf {Eval}_{int,\varPi }(\overline{C},\tilde{x}_b)=\tilde{C}(\tilde{x}_b)$.

Using the pigeon-hole principle and Eq. 1, for any $C\in \mathcal {C}_{\lambda }$ there exists $x^{*}$ such that,

$$\begin{aligned} |Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x^*)=C(x^*) | (\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C) ] \ge (1-1/\lambda ) \end{aligned}$$

(5)

Now substituting $x_1=x$ and $x_2=x^*$ in Eq. 4 and then plugging into Eq. 3 gives us,

$$\begin{aligned} \begin{aligned} |Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x)=C(x) |&(\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C)]-\\Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x^*)=C(x^*) |&(\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C)]|\le \mathsf {negl}(\lambda ) \end{aligned} \end{aligned}$$

(6)

Substituting result of Eq. 5 gives us the desired result. That is, For any circuit C and input x, it holds that,

$$\begin{aligned} \begin{aligned} |Pr[ \varPi '.\mathsf {Eval}(\mathsf {SP},\overline{C},x)=C(x) | (\mathsf {SP},\overline{C})\leftarrow {\varPi }'.\mathsf {Obf}(1^{\lambda },C) ] \ge&(1-1/\lambda ) -\mathsf {negl}(\lambda ) \\ >&(1-2/\lambda ) \end{aligned} \end{aligned}$$

(7)

This proves the result.

6.3 Instantiation of SFE

To instantiate SFE as described in Sect. 6.1, we use any single-key functional encryption scheme. To compute the circuit encoding for any circuit C we compute a function key for a circuit that has hard-wired a function key $sk_{H_C}$ for a circuit $H_C$ that takes as input (x, b) and outputs $C(x) \mathbin {\oplus }b$. This circuit uses the hard-wired function key to decrypt the input. To encode the input x, we just compute an FE encryption of (x, b). But this does not suffice, because then for any equivalent circuits $C_0$ and $C_1$, the circuit encodings are not equivalent. Hence, we use a one-time zero-knowledge proof system to prove that the cipher-text is consistent. The details follow next. Our decoding/evaluation operation is not randomized in contrast to [12], hence this allows us to directly argue security with polynomial loss, instead of going input by input.

Theorem 8

Assuming (non-compact) public-key functional encryption scheme for a single function key query exists, there exists an $\mathsf {SFE}$ according to the definition in Sect. 6.1.

Fig. 2.

Circuit H

Proof

Let $\mathsf {FE}$ denote any public-key functional encryption scheme for a single function key. Let $\mathsf {PZK}$ denote a non-interactive zero knowledge proof system with pre-processing. We now describe the scheme.

• $\mathsf {Setup}(1^{\lambda })$: The setup takes as input the security parameter $1^{\lambda }$. It first runs $(\mathsf {MPK},\mathsf {MSK})\leftarrow {\mathsf {FE}}.\mathsf {Setup}(1^{\lambda })$ and $\mathsf {PZK}.\mathsf {Pre}(1^{\lambda })\rightarrow (\sigma _{P},\sigma _{V})$. Output $\mathsf {SP}=(\mathsf {MPK},\mathsf {MSK},\sigma _P,\sigma _V)$.

• $\mathsf {CEncode}(\mathsf {SP},C)$: The algorithm on input $(\mathsf {SP}, C)$ does the following.

  • - Compute $sk_{H_C} \leftarrow \mathsf {FE}.\mathsf {KeyGen}(\mathsf {MSK},H_C)$. $H_C$ represents a circuit that on input (x, b) outputs $C(x) \mathbin {\oplus }b$.

  • - Let H be the circuit described in Fig. 2. Output H.

• $\mathsf {InpEncode}(\mathsf {SP},x)$: On input an $\mathsf {SP}$ and an input x do the following:

  • - Sample a random bit b and compute $\mathsf {CT}=\mathsf {FE}.\mathsf {Enc}(\mathsf {MPK},x,b;r_1)$.

  • - Compute the NIZK with pre-processing proof $\pi$ proving that $\mathsf {CT}\in L$ using the witness $(x,b,r_1)$.

  • - Output $((\mathsf {CT},\pi ),b)=(\tilde{x},b)$

• $\mathsf {Decode}(y,b)$: Output $y \mathbin {\oplus }b$.

We now discuss the properties:

Correctness. It is straightforward to see correctness as it follows from the completeness of the proof system and correctness of the functional encryption scheme.

Functionality: Let $H_b$ denote an circuit encoding of circuit $C_b$ for $b\in \{0,1\}$ where $C_0$ and $C_1$ are equivalent circuits. The circuit takes as input $(\mathsf {CT},\pi )$ where $\pi$ is a proof that $\mathsf {CT}$ is an encryption of $(x,b')$ for some x and a bit $b'$. Then it verifies the proof and decrypts the cipher-text using a function key that computes $C_b(x) \mathbin {\oplus }b'$. Since, the proof system is statistically sound and FE scheme is correct this property is satisfied with overwhelming probability over the coins of the setup.

Input Secrecy: We want to show that for any circuit C and inputs $x_0,x_1$:

$$\{(H,\tilde{x}_0) |H\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C), \mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda }), (\tilde{x}_0,z) \leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x_0) \} \approx _c$$

$$ \{(H,\tilde{x}_1) |H\leftarrow {\mathsf {CEncode}}(\mathsf {SP},C), \mathsf {SP}\leftarrow {\mathsf {Setup}}(1^{\lambda }), (\tilde{x}_1,z)\leftarrow {\mathsf {InpEncode}}(\mathsf {SP},x_1) \}$$

We claim this in a number of hybrids. The first one corresponds to the actual game where $\tilde{x}_0$ is given while the last one corresponds to the case of $\tilde{x}_1$. We also show that the hybrids are indistinguishable.

 

$\mathsf {Hyb}_0:$ :

This hybrid corresponds to the following experiment for $C,x_0$. To run setup we run $(\mathsf {MPK},\mathsf {MSK})\leftarrow {\mathsf {FE}}.\mathsf {Setup}(1^{\lambda })$. Then we sample a random bit b and compute $\mathsf {CT}\leftarrow {\mathsf {FE}}.\mathsf {Enc}(\mathsf {MPK},x_0,b)$. We sample $(\sigma _P,\sigma _V)\leftarrow {\mathsf {PZK}}.\mathsf {Pre}(1^{\lambda })$ and compute a proof $\pi$ using $\mathsf {PZK}$ prover string $\sigma _P$ and a witness of $\mathsf {CT}\in L$. We output $\mathsf {SP}=(\mathsf {MPK},\mathsf {MSK},\sigma _P,\sigma _V)$. This $\mathsf {SP}$ is used to encode C by computing a functional encryption key for circuit $H_C$ first ($sk_{H_C}$). Call this circuit H (this circuit depends upon, $\sigma _V$ and $sk_{H_C}$).

$\mathsf {Hyb}_1:$ :

This hybrid is the same as the previous one except that we generate $\pi ,\sigma _V$ differently. We run the simulator of $\mathsf {PZK}$ system and compute $(\sigma _V,\pi )\leftarrow {S}im(\mathsf {CT})$. $\mathsf {Hyb}_0$ is indistinguishable to $\mathsf {Hyb}_1$ due to the zero-knowledge security of $\mathsf {PZK}$ proof.

$\mathsf {Hyb}_2:$ :

This hybrid is the same as the previous one except that we generate $\mathsf {CT}$ differently. $\mathsf {CT}=\mathsf {FE}.\mathsf {Enc}(\mathsf {MPK},x_1,b\mathbin {\oplus }C(x_0) \mathbin {\oplus }C(x_1) )$. $\mathsf {Hyb}_1$ is indistinguishable to $\mathsf {Hyb}_2$ due to the security of $\mathsf {FE}$ proof.

$\mathsf {Hyb}_3:$ :

This hybrid is the same as the previous one except that $(\sigma _P,\sigma _V)$ are generated honestly. $\mathsf {Hyb}_2$ is indistinguishable to $\mathsf {Hyb}_3$ due to the zero-knowledge security of $\mathsf {PZK}$.

$\mathsf {Hyb}_4:$ :

This hybrid is the same as the previous one except that $\mathsf {CT}$ is generated as $\mathsf {FE}.\mathsf {Enc}(\mathsf {MPK},x_1,b )$. this corresponds to the experiment for input $x_1$. $\mathsf {Hyb}_3$ is identical to $\mathsf {Hyb}_4$ as b is a random bit.

 

Corollary 2

Assuming public-key encryption exists [45], there exists an SFE scheme satisfying requirements described in Sect. 6.1.

Remark 7

We note that such a scheme can be instantiated from one-way functions alone. The idea is to use a secret-key functional encryption for single function query along with a statistically binding commitment scheme. The public parameters now include a commitment of a master secret key which is used to proof consistency of the cipher-text. Since the end result of constructing public key functional encryption from IO candidates itself imply PKE, we do not describe this construction.

6.4 Robust Combiner: Construction

We now describe our robust combiner. On input the candidates $\varPi _1,..,\varPi _n$, we transform them using the $\mathsf {SFE}$ scheme as done in Sect. 6.2 so that they are $(1-1/\lambda )-$worst-case correct. Then using majority trick as in [12], we convert them to almost correct. Plugging it to the construction in Sect. 5.2, gives us the desired result. Finally, we also state our theorem about universal obfuscation.

Theorem 9

Assuming sub-exponentially secure one-way functions, there exists a $(\mathsf {poly},\epsilon )$-Universal Obfuscation with $\epsilon =O(2^{-\lambda ^c})$ for any constant $c>0$ and any polynomial $\mathsf {poly}$.