Abstract
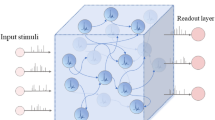
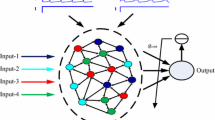
In recent years, increasing studies have shown that the networks in the brain can reach a critical state where dynamics exhibit a mixture of synchronous and asynchronous firing activity. It has been hypothesized that the homeostatic level balanced between stability and plasticity of this critical state may be the optimal state for performing diverse neural computational tasks. Motivated by this, the role of critical state in neural computation based on liquid state machines (LSM), which is one of the neural network application model of liquid computing, has been investigated in this note. Different from a randomly connect structure in liquid component of LSM in most studies, the synaptic weights among neurons in proposed liquid are refined by spike-timing-dependent plasticity (STDP); meanwhile, the degrees of neurons excitability are regulated to maintain a low average activity level by Intrinsic Plasticity (IP). The results have shown that the network yield maximal computational performance when subjected to critical dynamical states.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Beggs, J.M., Plenz, D.: Neuronal avalanches in neocortical circuits. J. Neurosci. Off. J. Soc. Neurosci. 23(35), 11167–11177 (2003)
Chialvo, D.R.: Critical brain networks. Phys. A Stat. Mech. Appl. 340(4), 756–765 (2004)
De, A.L., Perronecapano, C., Herrmann, H.J.: Self-organized criticality model for brain plasticity. Phys. Rev. Lett. 96(2), 028107 (2006)
Beggs, J.M., Plenz, D.: Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J. Neurosci. Off. J. Soc. Neurosci. 24(22), 5216–5229 (2004)
Haldeman, C., Beggs, J.M.: Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys. Rev. Lett. 94(5), 058101 (2005)
Kinouchi, O., Copelli, M.: Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2(5), 348–351 (2006)
Goh, K.I., Lee, D.S., Kahng, B., Kim, D.: Sandpile on scale-free networks. Phys. Rev. Lett. 91(14), 148701 (2003)
Pasquale, V., Massobrio, P., Bologna, L.L., Chiappalone, M., Martinoia, S.: Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience 153(4), 1354–1369 (2008)
Lin, M., Chen, T.: Self-organized criticality in a simple model of neurons based on small-world networks. Phys. Rev. E 71(1), 016133 (2005)
Pajevic, S., Plenz, D.: Efficient network reconstruction from dynamical cascades identifies small-world topology of neuronal avalanches. PLoS Comput. Biol. 5(1), e1000271 (2009)
Wang, S.J., Zhou, C.: Hierarchical modular structure enhances the robustness of self-organized criticality in neural networks. New J. Phys. 14(2), 023005 (2012)
Wang, S.J., Hilgetag, C., Zhou, C.: Sustained activity in hierarchical modular neural networks: self-organized criticality and oscillations. Front. Comput. Neurosci. 5, 30 (2011)
Natschläger, T., Maass, W., Markram, H.: The “liquid computer”: a novel strategy for real-time computing on time series. In: Special issue on Foundations of Information Processing of TELEMATIK, vol. 8 (LNMC-ARTICLE-2002-005), pp. 39–43 (2002)
Markram, H., Lübke, J., Frotscher, M., Sakmann, B.: Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275(5297), 213–215 (1997)
Xue, F., Hou, Z., Li, X.: Computational capability of liquid state machines with spike-timing-dependent plasticity. Neurocomputing 122, 324–329 (2013)
Li, X., Small, M.: Enhancement of signal sensitivity in a heterogeneous neural network refined from synaptic plasticity. New J. Phys. 12(8), 083045 (2010)
Daoudal, G., Debanne, D.: Long-term plasticity of intrinsic excitability: learning rules and mechanisms. Learn. Mem. 10(6), 456–465 (2003)
Marder, E., Abbott, L.F., Turrigiano, G.G., Liu, Z., Golowasch, J.: Memory from the dynamics of intrinsic membrane currents. Proc. Nat. Acad. Sci. 93(24), 13481–13486 (1996)
Triesch, J.: Synergies between intrinsic and synaptic plasticity in individual model neurons. In: NIPS, pp. 1417–1424 (2004)
Maass, W., Joshi, P., Sontag, E.D.: Computational aspects of feedback in neural circuits. PLoS Comput. Biol. 3(1), e165 (2007)
Izhikevich, E.M.: Simple model of spiking neurons. IEEE Trans. Neural Netw. 14(6), 1569–1572 (2003)
Shew, W.L., Yang, H., Yu, S., Roy, R., Plenz, D.: Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J. Neurosci. 31(1), 55–63 (2011)
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos. 61473051 and 61304165).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Li, X., Chen, Q., Xue, F., Zhou, H. (2017). The Critical Dynamics in Neural Network Improve the Computational Capability of Liquid State Machines. In: Cong, F., Leung, A., Wei, Q. (eds) Advances in Neural Networks - ISNN 2017. ISNN 2017. Lecture Notes in Computer Science(), vol 10261. Springer, Cham. https://doi.org/10.1007/978-3-319-59072-1_47
Download citation
DOI: https://doi.org/10.1007/978-3-319-59072-1_47
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-59071-4
Online ISBN: 978-3-319-59072-1
eBook Packages: Computer ScienceComputer Science (R0)